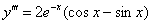Мы научимся находить производные высших порядков, а также записывать общую формулу «энной» производной. Кроме того, будет рассмотрена формула Лейбница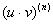 
таковой производной.
Вот функция: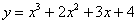 
и вот её первая производная:
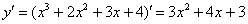
Нетрудно даже догадаться, что вторая производная – это производная от 1-й производной:
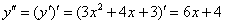
В принципе, вторую производную уже считают производной высшего порядка.
Аналогично: третья производная – это производная от 2-й производной:
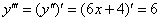
Четвёртная производная – есть производная от 3-й производной:
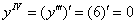
Пятая производная: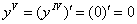 
, и очевидно, что все производные более высоких порядков тоже будут равны нулю:
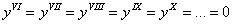
Помимо римской нумерации на практике часто используют следующие обозначения:
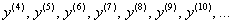, производную же «энного» порядка обозначают через 
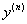. При этом надстрочный индекс нужно обязательно заключать в скобки – чтобы отличать производную от «игрека» в степени.
Иногда встречается такая запись: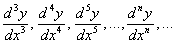 
– третья, четвёртая, пятая, …, «энная» производные соответственно.
Вперёд без страха и сомнений:
Пример 1
Дана функция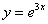 
. Найти 
.
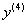Решение: что тут попишешь… – вперёд за четвёртой производной:
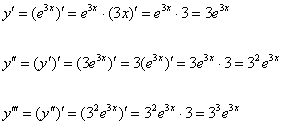
Четыре штриха ставить уже не принято, поэтому переходим на числовые индексы:
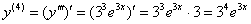
Ответ: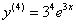 
Хорошо, а теперь задумаемся над таким вопросом: что делать, если по условию требуется найти не 4-ю, а например, 20-ю производную? Если для производной 3-4-5-го (максимум, 6-7-го) порядка решение оформляется достаточно быстро, то до производных более высоких порядков мы «доберёмся» ой как не скоро. Не записывать же, в самом деле, 20 строк! В подобной ситуации нужно проанализировать несколько найдённых производных, увидеть закономерность и составить формулу «энной» производной. Так, в Примере №1 легко понять, что при каждом следующем дифференцировании перед экспонентой будет «выскакивать» дополнительная «тройка», причём на любом шаге степень «тройки» равна номеру производной, следовательно:
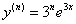, где 
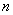– произвольное натуральное число.
И действительно, если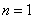 
, то получается в точности 1-я производная: 
, если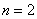 
– то 2-я: 
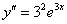и т.д. Таким образом, двадцатая производная определяется мгновенно: 
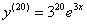– и никаких «километровых простыней»!
Пример 2
Найти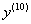 
для функции 
.
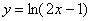Решение: чтобы прояснить ситуацию найдём несколько производных:
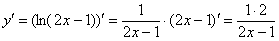
Полученные числа перемножать не спешим!
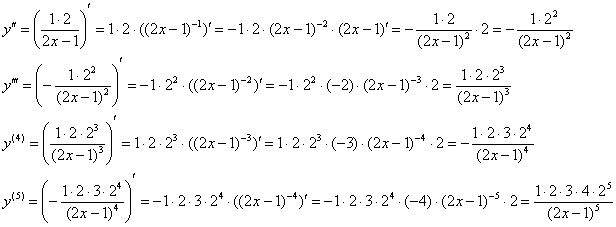
Пожалуй, хватит. …
На следующем шаге лучше всего составить формулу «энной» производной (коль скоро, условие этого не требует, то можно обойтись черновиком). Для этого смотрим на полученные результаты и выявляем закономерности, с которыми получается каждая следующая производная.
Во-первых, они знакочередуются. Знакочередование обеспечивает «мигалка», и поскольку 1-я производная положительна, то в общую формулу войдёт следующий множитель: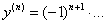 
. Подойдёт и эквивалентный вариант 
.
Во-вторых, в числителе «накручивается» факториал, причём он «отстаёт» от номера производной на одну единицу: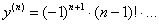 
И в-третьих, в числителе растёт степень «двойки», которая равна номеру производной. То же самое можно сказать о степени знаменателя. Окончательно:
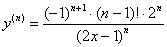
В целях проверки подставим парочку значений «эн», например,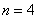 
и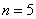 
:
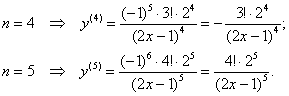
Замечательно, теперь допустить ошибку – просто грех:
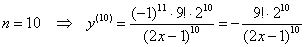
Ответ: 
Пример 3
Найти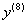 
функции 
.
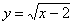Ещё раз повторим порядок действий:
1) Сначала находим несколько производных. Чтобы уловить закономерности обычно хватает трёх-четырёх.
2) Затем настоятельно рекомендую составить (хотя бы на черновике) «энную» производную – она гарантированно убережёт от ошибок. Но можно обойтись и без 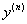, т.е. мысленно прикинуть и сразу записать, например, двадцатую или восьмую производную. Более того, некоторые люди вообще способны решить рассматриваемые задачи устно. Однако следует помнить, что «быстрые» способы чреваты, и лучше перестраховаться.
3) На заключительном этапе выполняем проверку «энной» производной – берём пару значений «эн» (лучше соседних) и выполняем подстановку. А ещё надёжнее – проверить все найдённые ранее производные. После чего подставляем в 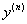нужное значение, например, 
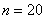или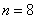 
и аккуратно причёсываем результат.
В некоторых задачах, во избежание проблем, над функцией нужно немного поколдовать:
Пример 4
Записать формулу производной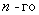 
порядка для функции 
Решение: дифференцировать предложенную функцию совсем не хочется, поскольку получится «плохая» дробь, которая сильно затруднит нахождение последующих производных.
В этой связи целесообразно выполнить предварительные преобразования: используем формулу разности квадратов и свойство логарифма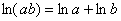 
:
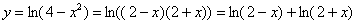
Примечание: в данном случае это свойство срабатывает для всех «икс» из области определения функции, и поэтому мы получаем равносильное преобразование.
Совсем другое дело:
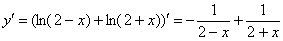
И старые подруги:
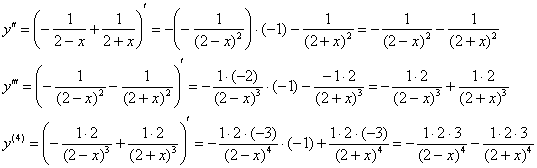
Обратите внимание, что 2-я дробь знакочередуется, а 1-я – нет. Конструируем производную 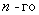порядка:
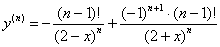
Контроль:
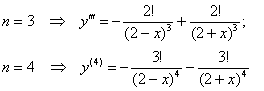
Ну и для красоты вынесем факториал за скобки:
Ответ: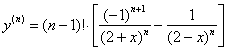 
А сейчас о незыблемой круговой поруке, которой позавидует даже итальянская мафия:
Пример 5
Дана функция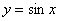 
. Найти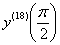 
Восемнадцатая производная в точке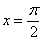 
. Всего-то.
Решение: сначала, очевидно, нужно найти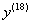 
. Поехали:
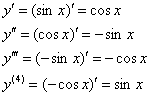
С синуса начинали, к синусу и пришли. Понятно, что при дальнейшем дифференцировании этот цикл будет продолжаться до бесконечности, и возникает следующий вопрос: как лучше «добраться» до восемнадцатой производной?
Способ «любительский»: быстренько записываем справа в столбик номера последующих производных:
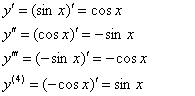
Таким образом: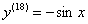 
Но это работает, если порядок производной не слишком велик. Если же надо найти, скажем, сотую производную, то следует воспользоваться делимостью на 4. Сто делится на 4 без остатка, и легко видеть, что таковые числа располагаются в нижней строке, поэтому: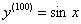 
.
Кстати, 18-ю производную тоже можно определить из аналогичных соображений:
во второй строке находятся числа, которые делятся на 4 с остатком 2.
Другой, более академичный метод основан на периодичности синуса и формулах приведения. Пользуемся готовой формулой «энной» производной синуса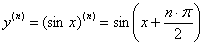 
, в которую просто подставляется нужный номер. Например:
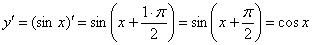( формула приведения 
);
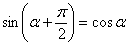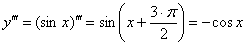( формула приведения 
)
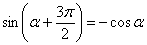В нашем случае:
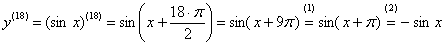
(1) Поскольку синус – это периодическая функция с периодом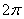 
, то у аргумента можно безболезненно «открутить» 4 периода (т.е. 
).
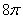(2) Пользуемся формулой приведения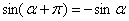 
.
С сотней, к слову, вообще всё элементарно – 25 «оборотов» прочь: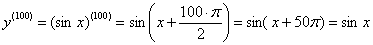 
Заключительная, более лёгкая часть задания – это нахождение восемнадцатой производной в точке:
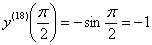
Ответ: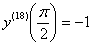 
Производным высших порядков от произведения функций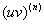 
Материал разберём на конкретной задаче:
Найти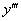 
функции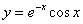 
Решение начнём с ключевого вопроса: как выгоднее всего найти третью производную от произведения функций?
…А почему бы, собственно, не взять три производные подряд? Тем более это представляется вполне подъёмной задачей. Используем правило дифференцирования произведения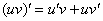 
и упрощаем результат:
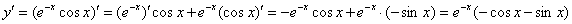
Со второй производной дела обстоят похуже, но всё-таки ещё не так плохи:
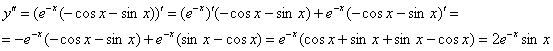
С третьей немножко повезло:
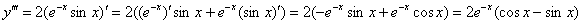
Всё выглядит весьма благонадёжно, но…
В чём недостаток такого решения? Во-первых, оно длинное. А ведь предложенная функция даже без «наворотов». И, во-вторых, тут легко запутаться (особенно в знаках). Рассмотрим простой и чёткий способ решения подобных заданий:
Формула Лейбница
Пожалуйста, не путайте с более известной формулой Ньютона-Лейбница!
Производную 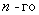порядка от произведения двух функций можно найти по формуле:
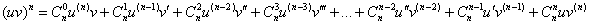
В частности:
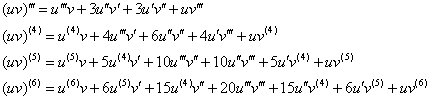
Примечание: здесь и далее предполагается дифференцируемость функций нужное количество раз
Специально запоминать ничего не надо, ибо, чем больше формул знаешь – тем меньше понимаешь. Гораздо полезнее ознакомиться с биномом Ньютона, поскольку формула Лейбница очень и очень на него похожа. Ну а те везунчики, которым достанется производная 7-го либо более высоких порядков (что, правда, маловероятно), будут вынуждены это сделать. Впрочем, когда черёд дойдёт до комбинаторики – то всё равно придётся
Найдём третью производную функции 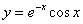. Используем формулу Лейбница:
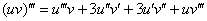
В данном случае: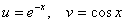 
. Производные легко перещёлкать устно:
Теперь аккуратно и ВНИМАТЕЛЬНО выполняем подстановку и упрощаем результат:
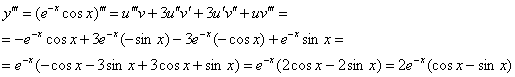
Ответ: 