, (1)
где 
, или 
- ряд с комплексными числами
Если существует 
, то ряд (1) называется сходящимся, и 
, иначе ряд (1) – расходящийся.
Теорема 1. Для сходимости ряда (1) необходимо и достаточно, чтобы сходились ряды 
и 
с действительными членами.
Теорема 2. Если сходится ряд 
, составленный из модулей членов ряда (1), то сходится и ряд (1), который называется при этом абсолютно сходящимся.
Функциональным рядом называется ряд
, (2)
где 
- функции комплексного переменного.
Если в каждой точке 
области 
ряд (2) сходится, то ряд (2) сходится в области , а сумма ряда 
определяется в этом случае как некоторая функция от ( - область сходимости ряда): 
, где 
.
Если ряд (2) сходится в области , то в каждой точке этой области последовательности остатков 
ряда стремится к нулю: 
.
Степенным рядом называется ряд вида
, (3)
где 
- комплексные числа (коэффициенты ряда), - комплексная переменная, или ряд
(4)
ТеоремаАбеля. Если степенной ряд (3) сходится в некоторой точке 
, то он абсолютно сходится в круге 
. Во всяком замкнутом круге меньшего радиуса 
ряд (3) сходится равномерно. Если ряд расходится при 
, то он расходится и при любом значении , для которого 
.
Из теоремы Абеля следует, что для всякого степенного ряда (3) существует круг с центром в начале координат, во всех точках которого ряд (3) сходится.
Радиус этого круга называется радиусом сходимости степенного ряда и определяется по формуле 
или 
.
Теорема. Функция 
, аналитическая в круге 
, может быть в этом круге единственным образом разложена в степенной ряд Тейлора 
,
где коэффициенты вычисляются по формулам 
.
Итак, ряд Тейлора для функции имеет вид: 
.
Замечание: Имеют место, как и в действительном анализе, аналогичные разложения в ряд основных элементарных функций, например, при 
,
,
,
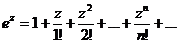
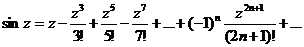
и др.
Рядами Тейлора представляются функции, аналитические в круговых областях. Часто приходится рассматривать функции, аналитичные всюду в некоторой окрестности точки 
, исключая саму точку , т.е. аналитичные в кольце 
. Такие функции представляются двусторонними рядами, содержащими как целые положительные, так и целые отрицательные степени 
. Эти ряды, названные по имени французского математика П.. Лорана (1813-1854), являются обобщением степенных рядов и имеют вид
, (5)
где 
(6)
- любой контур, принадлежащий рассматриваемому кольцу.
Теорема. всякая функция , аналитическая в круговом кольце , может в этом кольце единственным образом раскладываться в ряд Лорана (5), который в этом кольце абсолютно сходится.
Ряд 
называется правильной (регулярной) частью ряда Лорана.
Ряд 
называют главной (сингулярной) частью ряда Лорана.
Замечание 1. Интеграл 
нельзя заменить на 
, так как , вообще говоря, не аналитична в точке .
Замечание 2. Если функция является аналитической не только в кольце, но и в точке 
, т.е. аналитична в круге 
, то при всех 
подынтегральная функция в интеграле 
не имеет особых точек внутри , в силу чего по теореме Коши все 
и главная часть ряда Лорана исчезает. В этом случае 
и ряд Лорана превращается в ряд Тейлора, который, таким образом, является частным случаем ряда Лорана.
Замечание 3. Формула (6) приводит к громоздким выкладкам, поэтому на практике для нахождения коэффициентов используют, по возможности, уже известные разложения в ряд.