Методы Эйлера для решения задачи Коши.
Метод Эйлера первого порядка точности.
В методе Эйлера решение уравнения (2.4) представляется следующим образом:
 (2.6)
(2.6)
где  ,
, 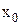 - начальная точка,
- начальная точка,  - шаг между узлами xi и xi+1,
- шаг между узлами xi и xi+1,  - значение искомой функции y(x) в узле xi,
- значение искомой функции y(x) в узле xi,  . При i=0 имеем:
. При i=0 имеем:

 (2.7)
(2.7)
где y0=y(x0) - начальное значение искомой функции y(x).
Абсолютная погрешность метода Эйлера на n шаге равна:
 (2.8)
(2.8)
где c1 и c2 - константы, R0 - погрешность начального приближения.
Согласно (2.8) метода Эйлера имеет первый порядок точности.
Модификации метода Эйлера второго порядка точности.
а) метод трапеции. В этом методе решение имеет вид:
 (2.9)
(2.9)
Этот метод неявный, т.к. для определения значений yi+1 необходимо решать нелинейное уравнение (2.9). Метод трапеций имеет второй порядок точности по h.
б) метод Эйлера-Коши. Данный метод является прямым методом второго порядка точности:
 (2.10)
(2.10)
в) усовершенствованный метод Эйлера второго порядка точности:
 (2.11)
(2.11)
Методы Рунге-Кутты для задачи Коши.
а) расчетам формулы метода Рунге-Кутты второго порядка точности имеют следующий вид:
 (2.12)
(2.12)
Данный метод является двух этапным. Вначале вычисляется значение k(1), а затем значения k(2).
При a=1 формулы (2.12) дают метод Эйлера-Коши, при a=1/2 - усовершенствованный метод Эйлера.
б) метод Рунге-Кутты четвертого порядка точности. Наиболее известным из методов Рунге-Кутты является классический 4-этапный метод четвертого порядка точности:
 (2.13)
(2.13)
Этот метод прост и эффективен, когда отрезок [x0,xn] не очень велик.
в) метод Рунге-Кутты четвертого порядка точности для системы из 2-х уравнений. Имеется система из двух дифференциальных уравнений:

Расчетные формулы для вычисления значений функции y(x) и z(x) имеют следующий вид:
 (2.15)
(2.15)
где
 (2.16)
(2.16)
4. Автоматический выбор шага. Локальная погрешность методов Рунге-Кутты точности p на i+1 шаге допускает представление:
 (2.17)
(2.17)
где r(xi,yi) - непрерывная функция, p - порядок точности.
Следовательно, можем записать:
 (2.17)
(2.17)
Здесь y(xi+1)-точное решение,  -приближенное решение с шагом h.
-приближенное решение с шагом h.
Уменьшим шаг интегрирования в два раза. Для вычисления значения функции y(xi+1) нам потребуется два шага. На первом шаге погрешность будет равна:

а на втором:

Суммарная погрешность после двух шагов по hi/2 будет равна сумме погрешностей на двух шагах:
 (2.18)
(2.18)
Следовательно, можем записать:
 (2.19)
(2.19)
здесь y(xi+1) - точное решение,  - приближенное решение с шагом hi/2.
- приближенное решение с шагом hi/2.
Вычитая из равенства (2.17) равенство (2.19) получим:
 (2.20)
(2.20)
Окончательно имеем:
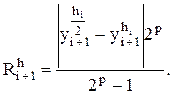 (2.21)
(2.21)
Если погрешность 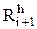 отличается от заданной погрешности R, то шаг h заменяют на новый шаг `h, например, уменьшают или увеличивают в два раза.
отличается от заданной погрешности R, то шаг h заменяют на новый шаг `h, например, уменьшают или увеличивают в два раза.
III. ЗАДАНИЕ.
1. Разработать текст программы для решения задачи Коши для системы из двух дифференциальных уравнений методом Рунге-Кутты четвертого порядка точности.
2. Предусмотреть в программе контроль точности численного решения и автоматический выбор шага при заданной погрешности численного решения.
3. Решить задачу Коши для системы из двух дифференциальных уравнений из таблицы индивидуальных заданий.
IV. ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ.
1. Задание: Решить задачу Коши для системы линейных уравнений:
 (4.1)
(4.1)
где m-параметр на отрезке [a,b], a=0,b=100 при следующих начальных условиях
 (4.2)
(4.2)
с абсолютной точностью e=10-4 при m=0.1.
2. Для решения задачи Коши будем использовать метод Рунге-Кутты четвертого порядка точности. В расчетных формулах (2.15, 2.16) имеем:
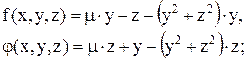
3. Пример программ на Delphy (в консольном режиме) и на Mathcad.
program lab10;
{Решение Задачи Коши для системы из двух уравнений}
{методом Рунге-Кутты четвертого порядка точности}
{a - начало отрезка, где необходимо найти решение}
{b - конец отрезка, где необходимо найти решение}
{y0,z0 - начальные условия}
{e - точность вычисления}
{h0 - начальное значение шага}
var a,b,y0,z0,e,h0,x,h,k1,k2,k3,k4,q1,q2,q3,q4: real;
var u,xx,yy,zz,yh,zh,yhh,zhh,ry,rz,m: real;
var i,p,j,kk,mm: integer;
var x,y,z: array [0..5000] of real;
var outfile: text;
label m1,m2;
function f(x,y,z: real): real;
{функция трех переменных f(x,y,z)}
Begin
 формула (4.1)
формула (4.1)
end; {f}
function g(x,y,z: real): real;
{функция трех переменных}
Begin
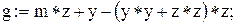 формула (4.1)
формула (4.1)
end; {g}
Begin
assign (outfile,’d:\lab.dat’); объявление внешнего файла lab.dat
rewrite (outfile); открытие внешнего файла для записи
writeln (‘Введите значение a и значение b’);
readln (a,b);
writeln (‘Введите значение y0 и значение z0’);
readln (y0,z0);
writeln (‘Введите точность вычислений e’);
readln (e);
writeln (‘Введите шаг h0’);
readln (h0);
p:=4;
i:=0;
x[0]:=a;
y[0]:=y0;
z[0]:=z0;
while x[i]<b do begin
i:=i+1;
kk:=0;
mm:=0;
m2: h:=h0;
xx:=x[i-1];
yy:=y[i-1];
zz:=z[i-1];
j:=0;
m1: k1:=f(xx,yy,zz);
q1:=g(x,yy,zz);
k2:=f(xx+h/2,yy+k1*h/2,zz+q1*h/2); формулы (2.16)
q2:=g(xx+h/2,yy+k1*h/2,zz+q1*h/2);
k3:=f(xx+h/2,yy+k2*h/2,zz+q2*h/2);
q3:=g(xx+h/2,yy+k2*h/2,zz+q2*h/2);
k4:=f(xx+h,yy+k3*h,zz+q3*h);
q4:=g(xx+h,yy+k3*h,zz+q3*h);
if j=0 then begin
yh:=yy+h*(k1+2*k2+2*k3+k4)/6; вычисление с шагом h
zh:=zz+h*(q1+2*q2+2*q3+q4)/6;
h:=h/2; уменьшение шага в два раза
j:=1;
goto m1; переход на вычисление с шагом h/2
end;
if j=1 then begin
yhh:=yy+h*(k1+2*k2+2*k3+k4)/6.; первый шаг с шагом h/2
zhh:=zz+h*(q1+2*q2+2*q3+q4)/6.;
xx:=xx+h;
yy:=yhh;
zz:=zhh;
j:=2;
goto m1; переход на второй шаг с шагом h/2
end;
if j=2 then begin
yhh:=yy+h*(k1+2*k2+2*k3+k4)/6; второй шаг с шагом h/2
zhh:=zz+h*(q1+2*q2+2*q3+q4)/6;
end;
u:=exp(p*ln(2)); вычисление 2 в степени p
ry:=(abs(yhh-yh)*u)/(u-1.);
rz:=(abs(zhh-zh)*u)/(u-1.);
if (kk=0) and (( ry>e) or (rz>e)) then begin
mm:=1;
h0:=h0/2; автоматическое уменьшение шага в два раза
goto m2;
end;
if (mm=0) and (( ry<e) and (rz<e)) then begin
kk:=1;
h0:=2*h0; автоматическое увеличение шага в два раза
goto m2;
end;
x[i]:=x[i-1]+h0;
y[i]:=yh;
z[i]:=zh;
writeln (‘i=’,i,’ h0=’,h0,’ x=’,x[i],’ y=’,y[i],’ z=’,z[i]);
writeln (outfile,‘i=’,i,’ h0=’,h0,’ x=’,x,’ y=’,y[i],’ z=’,z[i]);
end;
close (outfile); закрытие внешнего файла
End.



V. СОДЕРЖАНИЕ ОТЧЕТА.
1.Название лабораторной работы.
2.Индивидуальное задание.
3.Текст программы.
4.Таблица результатов расчета на ЭВМ.
Замечание: Пункты 1-4, а также таблица пункта 5 без численных результатов должны быть оформлены до начала выполнения лабораторной работы.
Результаты программы в Delphy нужно вывести в виде графика используя файл с данными и соответствующую программу для построения графиков.
VI. КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Что такое обыкновенное дифференциальное уравнение?
2. Какое дифференциальное уравнение называется разрешимым относительно старшей производной.
3. Что называется линейным дифференциальным уравнением?
4. Определение частного и общего решения дифференциального уравнения.
5. Задача Коши.
6. Краевая задача
7. Определение интегральной кривой.
8. Методы Эйлера первого и второго порядка точности.
9. Модификации метода Эйлера.
10. Методы Рунге-Кутты второго и четвертого порядка точности.
11. Методы Рунге-Кутты для систем дифференциальных уравнений.
12. Автоматический контроль погрешности и выбор шага численного решения.
13. Метод Адамса-Бошфорта.
14. Метод Адамса-Моултона.
15. Метод прогноза и коррекции.
16. Можно ли в методах Адамса контролировать точность расчетов с помощью изменения шага h?
VII. ТАБЛИЦА ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ.
Решить задачу Коши y¢=f(x,y,z), z¢=j(x,y,z); при y0=y(a), z0=z(a), на отрезке [a,b] с заданной абсолютной погрешностью e.
| № | f(x,y,z) | j(x,y,z) | y(a) | z(a) | a | b | e |
| 1. | 
| 
| -1 | 10-3 | |||
| 2. | 
| 
| 0,5 | 1,5 | 10-4 | ||
| 3. | 
| 
| -1 | 10-3 | |||
| 4. | 
| 
| 10-4 | ||||
| 5. | 
| 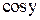
| 0,5 | -0,5 | 10-3 | ||
| 6. | 
| 
| -0,6 | 10-4 | |||
| 7. | 
| 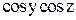
| -1 | 10-3 | |||
| 8. | 
| 
| 0,5 | 1,2 | 10-4 | ||
| 9. | 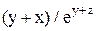
| 
| -1 | 10-3 | |||
| 10. | 
| 
| -3 | 10-4 | |||
| 11. | 
| 
| 10-3 | ||||
| 12. | 
| 
| -2 | -1 | 10-4 | ||
| 13. | 
| 
| -1 | 10-4 | |||
| 14. | 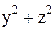
| 
| -1 | 10-3 | |||
| 15. | 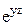
| 
| 10-4 | ||||
| 16. | 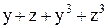
| 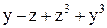
| 10-4 | ||||
| 17. | 
| - 
| -2 | 10-4 | |||
| 18. | 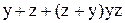
| 
| 10-3 | ||||
| 19. | 
| 
| 10-4 | ||||
| 20. | 
| 
| 10-3 |