Анализ сезонных колебаний динамического ряда
Под сезонными колебаниями понимают регулярные, периодические наступления внутригодовых подъемов и спадов производства, грузооборота, товарооборота и т.д.
Определение в рядах динамики индексов сезонности
1.1. Для ряда внутригодовой динамики, в которой не наблюдается тенденция роста (или она незначтельна), изучение сезонности основано на методе постоянной средней:
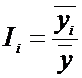(1), где 
- осредненные эмпирические уровни ряда по одноименным периодам; 
- общий средний уровень ряда.
Если в ряду внутригодовой динамики имеется ярко выраженная общая тенденция роста, то индексы сезонности определяются на основе методов, позволяющих исключить (элиминировать) влияние тенденции роста.
Пример 6.4. Анализ сезонных колебаний.
Имеются данные о распределении браков, заключенных населением города, по месяцам 1996-1998гг.
| Месяц | |||
| январь | |||
| февраль | |||
| март | |||
| апрель | |||
| май | |||
| июнь | |||
| июль | |||
| август | |||
| сентябрь | |||
| октябрь | |||
| ноябрь | |||
| декабрь | |||
| всего |
Для выявления характера общей тенденции данного ряда внутригодовой динамики произведем укрупнение месячных периодов в годовые уровни и определим темпы роста:
| Год | Годовые уровни | Темпы роста,% | |
| К предыдущему году | К 1996 | ||
| 103,505 | 103,505 | ||
| 103,984 | 104,629 |
По изменению уровней укрупненных периодов видно, что изучаемое явление не имеет значительной общей тенденции роста, поэтому определение индексов сезонности можно провести на основе метода постоянной средней:
Для получения значений 
по способу простой средней проведем усреднение уровней одноименных периодов за три года
, где 
- число календарных дней в усредняемых месячных периодах; это позволяет исключить несопоставимость уровней ряда в связи с различной продолжительностью месяцев. Определим осреденные значения для каждого месяца годового цикла.
Январь: 
Февраль: 
и т.д.
Далее по исчисленным месячным средним определим средний уровень:
Значение общего среднего уровня можно также получить и по итоговым данным за отдельные годы.
Определим индексы сезонности по формуле 1, полученные результаты занесем в таблицу
| Месяц | среднее число браков в день
| индексы сезонности
|
| январь | 5.741935 | 1.04037 |
| февраль | 6.45 | 1.182036 |
| март | 5.268817 | 0.954647 |
| апрель | 5.4 | 0.978415 |
| май | 4.634409 | 0.839699 |
| июнь | 5.011111 | 0.907953 |
| июль | 5.344086 | 0.968284 |
| август | 5.645161 | 1.022836 |
| сентябрь | 0.90594 | |
| октябрь | 5.387097 | 0.976077 |
| ноябрь | 6.133333 | 1.111287 |
| декабрь | 6.139785 | 1.112455 |
| Общий средний уровень | 1.00 |
Для большей наглядности сезонных колебаний средние индексы изображаются графически
1.2. Для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития можно применяется способ скользящей средней. Формула расчета индексов сезонности принимает вид:
, (2)
где 
- исходные уровни ряда; 
- сглаженные уровни ряда, n –число одноименных периодов.
Применение формулы (2) рассмотрим на данных о продаже продуктов сельскохозяйственного производства магазинами потребительской кооперации города. В таблице приведены исходные уровни объемов продаж (графа 1), сглаженные с помощью четырехзвенной скользящей средней уровни (графа 2)
В графе 4 исходные уровни yi сопоставлены с соответствующими уровнями . При использовании четырехзвенной скользящей средней расчет значений yi: начинается с III квартала первого года 326:274,24=1.318. Для четвертого квартала 297:287.6=1.033 и т.д.
| Год, квартал | Исходные уровни yi | Сглаженные уровни
| 
|
| 1 год | |||
| I | - | ||
| II | - | ||
| III | 274,25 | 1.318 | |
| IV | 287,6 | 1.033 | |
| 2 год | |||
| I | 297,0 | 0.832 | |
| II | 307,5 | 0.969 | |
| III | 334,6 | 1.094 | |
| IV | 374,1 | 0.911 | |
| 3 год | |||
| I | 402,9 | 1.042 | |
| II | 421,0 | 1.047 | |
| III | 429,0 | 1.056 | |
| IV | 430,75 | 0.926 | |
| 4 год | |||
| I | 435,37 | 0.978 | |
| II | 446,62 | 1.005 | |
| III | - | ||
| IV | - |
Для получения итоговых индексов сезонности 
производится осреднение исчисленных значений yi: 
по одноименным кварталам
Iкв - 
, или 95,1% IIкв - 
, или 100,7%
IIIкв - 
или 115,6 % IVкв - 
, или 95.7%
Исчисленные показатели являются средними индексами сезонных колебаний продажи продукции сельскохозяйственного производства по кварталам. Для наглядности сезонные колебания изображаются на графике
Рисунок. Сезонная волна товарооборота комиссионной торговли сельскохозяйственными продуктами (прирост в % к среднему уровню)
3. Сезонные колебания при отчетливо выраженной тенденции измеряются также и способом переменной средней.
Индексы сезонности при этом вычисляются как 
,
где yti - теоретические уровни тренда полученные по методу наименьших квадратов, например, для линейной функции yt=a0+a1t. Далее вычисления индексов сезонности проводятся по методике описанной в файле Моделирование сезонности.doc