Урок №
"Касательная плоскость к сфере.
Взаимное расположение касательной прямой к сфере"
Посмотрите видео https://www.youtube.com/watch?v=hHLyD8uswA4
https://www.youtube.com/watch?v=yZh0EhjmoEE
Выучите основной материал урока (пункт 66-67)
Разберите и запишите краткое решение задач. Не забудьте сделать рисунок, записать, что дано, что нужно найти, решение и ответ.
Выполните домашнее задание №583, 587
Задача: диаметр шара равен 18 см. На каком расстоянии от центра шара находится плоскость, касающаяся его?
Решение: напомним, что касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара. Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
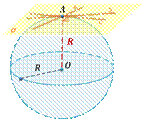
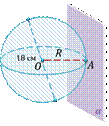По свойству касательной плоскости к сфере: радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости 
.
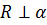Радиус нашего шара и будет расстоянием от центра шара до точки касания с плоскостью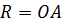 
.
Так как по условию задачи диаметр шара равен 18 см, то радиус равен 
(см). Запишем ответ.
Задача: сфера касается плоскости равностороннего треугольника с высотой 12 см в его центре. Расстояние от центра сферы до стороны треугольника равно 5 см. Найдите радиус сферы.
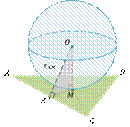Решение: так как по условию задачи треугольник равносторонний, то его центр будет находиться в центре вписанной и описанной окружностей.
Напомним, что в равностороннем треугольнике высота является и биссектрисой, и медианой. А по свойству медиан треугольника: три медианы треугольника пересекаются в одной точке, являющейся центром тяжести треугольника. Эта точка делит каждую медиану в отношении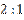 
, считая от вершины.
Так как по условию задачи высота треугольника равна 12 см, а она же является и медианой, значит, расстояние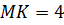 
(см).
Рассмотрим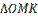 
. Он прямоугольный, так как 
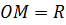. А по свойству касательной плоскости к сфере: радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Применим теорему Пифагора и найдем чему равен катет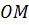 
. Получаем, что 
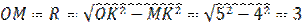(см).
Задача: расстояние от точки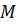 
до центра 
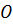сферы с радиусом 
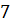см равно 
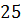. Найдите расстояние от данной точки до точки 
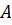касания прямой 
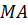и сферы.
Решение: соединим точку А, точку касания, с центром сферы.
Отрезок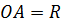 
. Напомним, что радиус, проведённый в точку касания прямой и сферы, перпендикулярен к касательной прямой.
Рассмотрим 
. Он прямоугольный. Применяя теорему Пифагора найдём чему равен катет 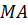, который и является расстоянием от точки 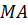до точки А. Имеем, 
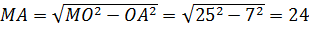(см).
Задача: шар пересечён плоскостью. Площадь сечения равна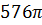 
см2. Расстояние от центра шара до плоскости сечения равно 7 см. Найдите радиус шара.
Решение: сечение шара плоскостью – круг, центр которого совпадает с основанием перпендикуляра, опущенного из центра шара на плоскость сечения.
Значит, из центра шара О проведём перпендикуляр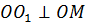 
. Затем соединим точк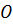и и 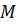. Получим прямоугольный треугольник 
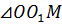, у которого гипотенуза .
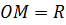По условию задачи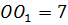 
см,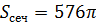 
см2. Так как площадь круга 
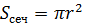, то получаем, что радиус сечения равен 
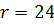(см).
Из прямоугольного треугольника 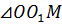по теореме Пифагора находим: 
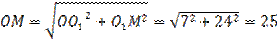(см). Запишем ответ.