Колебания маятника
Цель работы: изучение зависимости периода колебаний маятника от угла отклонения.
Оборудование: установка, электронный миллисекундомер.
Продолжительность работы - 4 часа.
Теоретическая часть. Описание установки
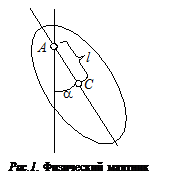Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной горизонтальной оси. Точка пересечения ее с вертикальной плоскостью, проходящей через центр масс маятника, называется точкой подвеса маятника (точка А на рис.1). Положение тела в каждый момент времени можно характеризовать углом отклонения его от положения равновесия 
. Кинетическая энергия качающегося физического маятника определяется выражением
,
где 
- момент инерции маятника относительно горизонтальной оси, проходящей через точку A; 
- угловая скорость. Потенциальная энергия маятника равна 
, где 
- высота подъема центра масс C над его самым нижним положением. Обозначим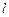 
- расстояние между центром масс C и точкой подвеса A. Тогда
,
и полная механическая энергия
. (1)
Если силами трения и сопротивления можно пренебречь, то механическая энергия остается постоянной, а следовательно,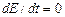 
. Продифференцировав (1), получим:
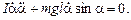
Отсюда имеем дифференциальное уравнение
, (2)
где 
.
В случае малых колебаний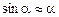 
, и в этом приближении из (2) получается дифференциальное уравнение
, (3) общее решение которого имеет вид:
. (4)
Не зависящие от времени величины 
(угловая амплитуда колебаний) и 
(начальная фаза) определяются начальными условиями, т.е. углом отклонения и угловой скоростью при 
. Колебания, описываемые формулой (4), называются гармоническими, а уравнение (3) называется дифференциальным уравнением гармонических колебаний.
Таким образом, малые колебания физического маятника будут приблизительно гармоническими с циклической частотой
и периодом
. (5)
Период колебаний (5) не зависит от амплитуды - такие колебания называются изохронными. Мы видим, что малые колебания физического маятника изохронны.
При больших амплитудах колебаний решение уравнения (2) не удается выразить в элементарных функциях. В подобных случаях обычно используют численные методы и компьютерные расчеты.
Рис.2. Зависимость угла отклонения физического маятника от времени
при различных угловых амплитудах колебаний 
На рис.2 приведены результаты численного решения уравнения (2) для нескольких значений амплитуды .
Видно, что при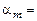 
10○ и 30○ период колебаний практически одинаков и примерно равен периоду малых колебаний 
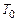, определяемому формулой (5). При 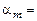90○ период колебаний 
превышает 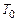почти на 20%, а при 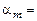150○ это превышение уже составляет 75%. Таким образом, изохронность колебаний маятника при больших амплитудах резко нарушается.
Заметим, что форма колебаний остается близкой к синусоидальной даже при очень больших амплитудах. Даже при 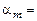150○ отклонение от синусоидальной формы весьма незначительно (пунктирная кривая на рис.2 рассчитана по формуле 
150○ 
, а при 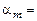90○ отклонений от синусоидальной зависимости при выбранном на рис.2 масштабе вообще не заметно. Итак, колебания остаются близкими по форме к синусоидальным по крайней мере при 
90○, но зависимость периода колебаний от амплитуды выражена достаточно отчетливо.
Получим приближенную формулу для периода колебаний, предположив, что колебания имеют синусоидальную (или близкую к ней) форму:
(6)
Неизвестную частоту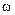 
можно было бы искать из условия обращения уравнения (2) в тождество при подстановке частного решения (6). Но так как синусоидальный закон (6) выполняется лишь приближенно, тождества при подстановке (6) в (2) не получится. Будем искать такое значение неизвестной частоты 
при котором отклонение левой части уравнения (2) от нуля минимально. Вычислим левую часть уравнения (2), обозначив ее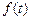 
:
.
Разложим 
в ряд:
(здесь дан в радианах). Поскольку при 
ряд быстро сходится, ограничимся двумя первыми членами. Применив тригонометрическое тождество
,
после простых преобразований получим:
.
Можно показать, что среднее квадратичное отклонение функции 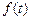от нуля
(
- период колебаний) минимально при
.
Отсюда следует
.
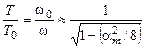Воспользовавшись разложением в ряд
при 
<< 
,
получим:
. (7)
Кривая, рассчитанная по формуле (7), изображена на рис.3 пунктирной линией, а график зависимости 
от , построенный по ре-
Рис.3. Зависимость периода колебаний от угловой амплитуды
зультатам точного численного решения уравнения (2), - сплошной линией. Видно, что при 
приближенная формула (7) дает значения периода, очень близкие к результатам точного расчета.
Выражение (7) проверяется в данной работе экспериментально.
Маятник представляет собой стальной шарик, подвешенный на двух нитях, которые фиксируют плоскость колебаний. К шарику прикреплен небольшой стержень, пересекающий в ходе колебаний луч света, падающий на фотодатчик. Электрический сигнал с фотодатчика управляет электронным секундомером. Секундомер включается при первом пересечении маятником светового луча фотодатчика и выключается при третьем пересечении. Этим достигается измерение периода колебаний. Точность электронного секундомера равна 0,001 с.
Заметим, что формула (7) получена в предположении, что колебания незатухающие, т.е. нет потерь механической энергии. В реальных условиях на маятник действует сила сопротивления воздуха, которую можно считать пропорциональной скорости движения маятника. Однако оценки показывают, что в условиях нашего эксперимента влияние силы сопротивления на период колебаний пренебрежимо мало.
Экспериментальная часть
Измерьте периоды колебаний маятника для пяти значений угла отклонения в диапазоне от 10○ до 40○. Для этого отклоните маятник и, убедившись, что он совершает колебания с нужной амплитудой, нажмите кнопку ²Сброс² - произойдет измерение периода колебаний. Проведите не менее трех измерений для каждого угла.
Обработку экспериментальных данных проведите в следующем порядке.
1. Постройте график зависимости от 
(напомним, что измеряется в радианах). Как следует из уравнения (7), эта зависимость должна быть линейной:
. (8)
Убедитесь в этом.
2. Продлите график до пересечения с осью ординат и найдите значение периода при 
. Как следует из (8), это значение равно .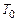
3. Отклонив маятник на угол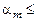 
5○, найдите экспериментальное значение 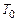. Сравните его со значением, полученным из графика.
4. Определите значение углового коэффициента 
полученной прямой. Как следует из (8), угловой коэффициент должен быть равен
.
При известном Т 0 рассчитайте теоретическое значение углового коэффициента 
и сравните с экспериментальным.
Литература 
1. Иродов И.Е. Механика. Основные законы. - М.: Физматлит, 2001. - § 6.1.
2. Савельев И.В. Курс общей физики. - М.: Астрель, 2001. - Т. 1. - §§ 8.1, 8.4, 8.5.