I. Практическое выполнение заданий
Для совершенствования навыков и умений решения заданий на нахождение промежутков возрастания и убывания функции, определения критических точек, а также нахождения наибольшего и наименьшего значения функции, выполним следующее задание: разбор примеров решение
Карточка №1
1. Найдите промежутки возрастания и убывания функции 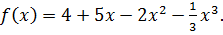
Решение
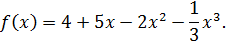
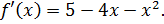
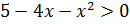
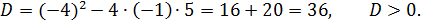
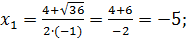
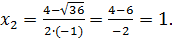
 |


 – + – x
– + – x
-5 1
Ответ: 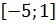 - возрастает,
- возрастает,
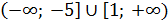 - убывает.
- убывает.
Карточка №2
1. Найдите критические точки функции 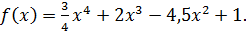
Решение
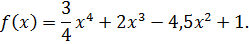
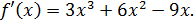
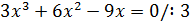
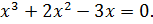
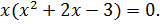
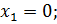
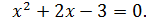
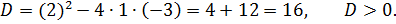
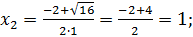
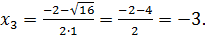
Ответ: 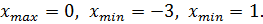
Карточка №3
1. Найдите наибольшее и наименьшее значения функции 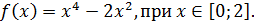
Решение
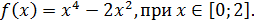
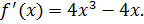
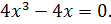
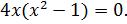
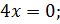
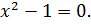
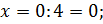
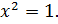
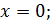
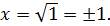
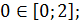
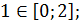
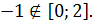
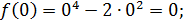
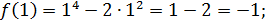
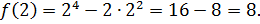
Ответ: 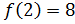 – наибольшее,
– наибольшее,
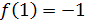 - наименьшее.
- наименьшее.
Карточка №4
1. Найдите промежутки возрастания и убывания функции 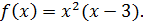
Ответ: 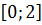 - убывает,
- убывает,
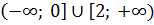 – возрастает.
– возрастает.
Карточка №5
1. Найдите критические точки функции 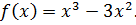
Ответ: 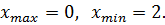
Затем следующее задание – выполнение тестовой работы. Всего в задании пять примеров, за каждый правильный пример, учащаяся получает один балл.
Тестовое задание
1. Найдите промежутки убывания функции 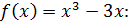
A) 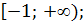 B)
B) 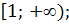 C)
C) 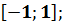 D)
D) 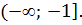
2. Найдите производную функции 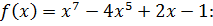
A) 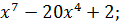 B)
B) 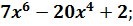
C) 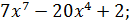 D)
D) 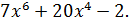
3. Найдите точки минимума функции 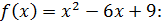
A) 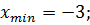 B)
B) 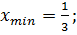 C)
C) 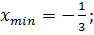 D)
D) 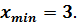
4. Вычислите наименьшее значение функции 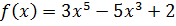 на отрезке
на отрезке 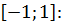
A) 0; B) 1; C) 2; D) 3.
5. Найдите производную функции 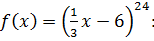
A) 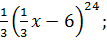 B)
B) 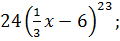 C)
C) 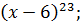 D)
D) 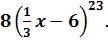
Как найти наибольшее и наименьшее значения функции на отрезке. Задание 12.
Как найти наибольшее и наименьшее значения функции на отрезке?
Для этого мы следуем известному алгоритму:
1. Находим ОДЗ функции.
2. Находим производную функции
3. Приравниваем производную к нулю
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции:
Если на промежутке I производная функции 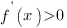
 , то функция
, то функция 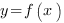 возрастает на этом промежутке.
возрастает на этом промежутке.
Если на промежутке I производная функции 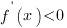
 , то функция
, то функция 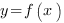 убывает на этом промежутке.
убывает на этом промежутке.
5. Находим точки максимума и минимума функции.
В точке максимума функции производная меняет знак с "+" на "-".
В точке минимума функции производная меняет знак с "-" на "+".
6. Находим значение функции в концах отрезка,
· затем сравниваем значение функции в концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции
· или сравниваем значение функции в концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции
Однако, в зависимости от того, как себя ведет функция на отрезке, это алгоритм можно значительно сократить.
Рассмотрим функцию 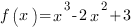 . График этой функции выглядит так:
. График этой функции выглядит так:
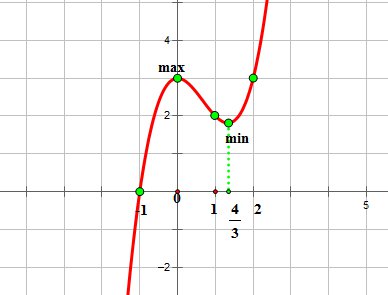 В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
1. Рассмотрим функцию на отрезке 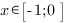
Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: 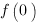 , а наименьшее - в левом:
, а наименьшее - в левом: 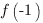 .
.
2. Рассмотрим функцию на отрезке 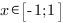
Очевидно, что наибольшее значение функция принимает в точке максимума 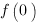 , а наименьшее - в одном из концов отрезка, то есть надо найти значения
, а наименьшее - в одном из концов отрезка, то есть надо найти значения 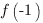 и
и 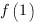 и выбрать из них наименьшее.
и выбрать из них наименьшее.
3. Если мы рассмотрим функцию на отрезке 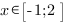 , то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть
, то чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и в правом конце отрезка, то есть 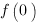 и
и 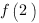 .
.
Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и в левом конце отрезка, то есть 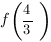 и
и 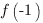 .
.
Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
1. ОДЗ функции 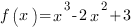 - множество действительных чисел.
- множество действительных чисел.
2. 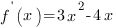
3. 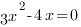 , если
, если 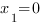 или
или 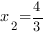
Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание - убывание, можно схематично изобразить ее график:
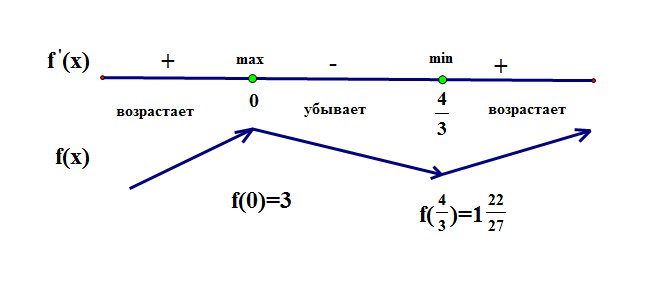
Рассмотрим несколько примеров решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике
Задание B15 (№ 26695)
Найдите наибольшее значение функции 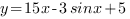 на отрезке
на отрезке 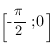 .
.
1. Функция 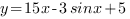 определена при всех действительных значениях х
определена при всех действительных значениях х
2. 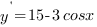
3. 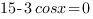
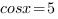 Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция
Очевидно, что это уравнений не имеет решений, и производная при всех значениях х положительна. Следовательно, функция 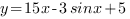 возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
возрастает и принимает наибольшее значение в правом конце промежутка, то есть при х=0.
y(0)=5
Ответ: 5.
2. Задание B15 (№ 26702)
Найдите наибольшее значение функции 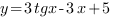 на отрезке [
на отрезке [ 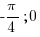 ].
].
1. ОДЗ функции 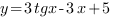
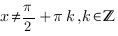
2. 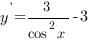
Производная равна нулю при 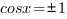 , однако, в этих точках она не меняет знак:
, однако, в этих точках она не меняет знак:

 , следовательно,
, следовательно, 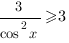
 , значит,
, значит, 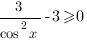
 , то есть производная при всех допустимых значених х неотрицательна, следовательно, функция
, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция 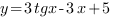 возрастает и принимает наибольшее значение в правом конце промежутка, при
возрастает и принимает наибольшее значение в правом конце промежутка, при 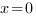 .
.
Чтобы стало очевидно, почему производная не меняет знак, преобразуем выражение для производной следующим образом:
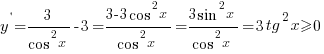
у(0)=5
Ответ: 5.
Задание B15 (№ 26708)
Найдите наименьшее значение функции 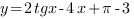 на отрезке [
на отрезке [ 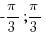 ].
].
1. ОДЗ функции 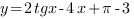 :
: 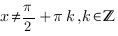

2. 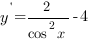
3. 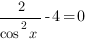
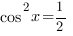 ,
, 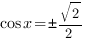
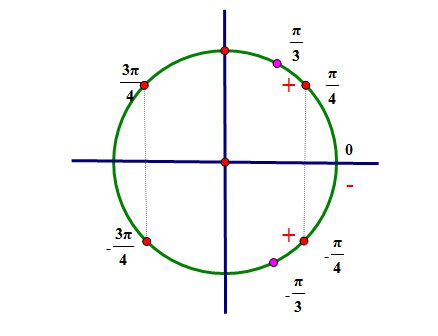
Расположим корни этого уравнения на тригонометрической окружности.
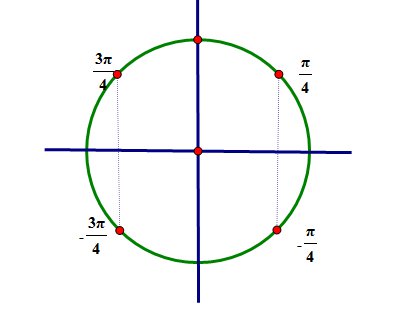
Промежутку 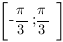 принадлежат два числа:
принадлежат два числа: 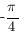 и
и 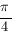
Расставим знаки. Для этого определим знак производной в точке х=0: 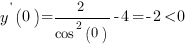
 . При переходе через точки
. При переходе через точки 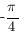 и
и 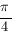 производная меняет знак.
производная меняет знак.
Изобразим смену знаков производной функции 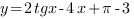 на координатной прямой:
на координатной прямой:
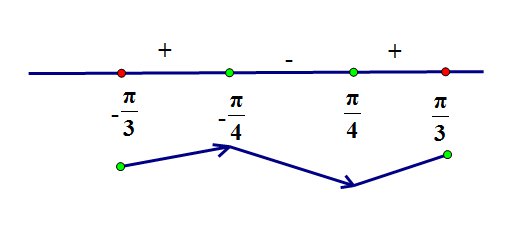
Очевидно, что точка 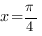 является точкой минимума (в ней производная меняет знак с "-" на "+"), и чтобы найти наименьшее значение функции
является точкой минимума (в ней производная меняет знак с "-" на "+"), и чтобы найти наименьшее значение функции 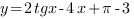 на отрезке
на отрезке 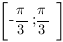 , нужно сравнить значения функции в точке минимума и в левом конце отрезка,
, нужно сравнить значения функции в точке минимума и в левом конце отрезка, 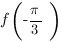 .
.
Схитрим: так как результат должен быть целым числом, или конечной десятичной дробью, а 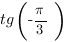 таковым на является, следовательно подставим в уравнение функции
таковым на является, следовательно подставим в уравнение функции 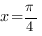
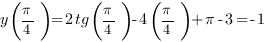
Ответ: -1