Лабораторная работа №1
(Оформляется в MS WORD. Титульный лист должен содержать ФИО, № группы, вариант)
ЛР1. Основы Scilab. Задачи с одномерными массивами
| plot(x,y) | построение графика функции y(x) |
| plot(x,y1,x,y2) | построение графиков функций y1(x) и y2(x) в одной системе координат |
| xbasc(),xclear() | очистить графическое окно |
| plot2d2(x,y) | построение графика в виде ступенчатой линии |
| polarplot(fi,ro) | построение графиков в полярной системе координат |
| plot3d(x,y,z) | построение графика z=z(x,y) |
| [x,y]=meshgrid([]) | создание прямоугольной сетки |
Задания.
В заданиях n – номер студента в списке.
1.Построить графики функций в прямоугольной декартовой системе координат (некоторые графики построить в одной системе координат и в виде ступенчатой линии. y=sinx/x
1. y=xn-10-5x+n;
2. y=tg(nx)+n;
3. y=x+sin(x)+ctgx+lnx+e2x;
4. y=x3cos2x
5. y=x2 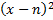
Построить график параметрической кривой 
Построить графики функций в полярной системе координат.
1. r=n 
2. r=n 
3. r=2-4sin  ;
;
4. r=sin  ;
;
5. r=sin  1.75
1.75  ;
;
6. r=  ;
;
7. r=  ;
;
8. r=  ;
;
Построить график функции  , x меняется от –
, x меняется от –  до
до  с шагом
с шагом 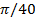 .
.
3. Даны матрицы:
 ,
,  , C
, C 
Найти (3*(A  B+C))*(A-C), (A+B)*(A+C), (A-B)*(B+C).
B+C))*(A-C), (A+B)*(A+C), (A-B)*(B+C).
4. Для всех уравнений отделить корни графически. То есть, с помощью графика функции для каждого корня уравнения подобрать отрезок, содержащий только этот корень. Решить уравнения:
 +8x
+8x  10=0;
10=0;
 -8x
-8x  2=0;
2=0;
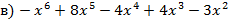 +8x
+8x  7=0;
7=0;
 4x
4x  5=0;
5=0;
 +18x=1;
+18x=1;
Матричные операции линейной алгебры в Scilab.
| length(x) | количество элементов в массиве |
| [n, m]=size (A) | количество строк(n), столбцов(m) матрицы А |
| A(:,j) | j-й столбец матрицы A |
| A (i,:) | i-я строка матрицы A |
| A(j:k) | элементы aj, aj+1, …, ak |
| A (:) | записывает все элементы матрицы A в виде столбца |
| A (m,:) = [ ] | удаляет из матрицы A строку с номером m |
| A’ | транспонированная матрица |
| prod(x) | произведение всех элементов массива A |
| prod(A,dim) | произведение элементов столбцов (dim=1) или строк (dim=2) |
| sum(A) | сумма всех элементов массива A |
| sum(A,dim) | сумма элементов столбцов (dim=1) или строк (dim=2) |
| det(A) | определитель квадратной матрицы A |
| rank(A) | ранг матрицы A |
| inv (A) | матрица, обратная матрицеA |
5. Применить рассмотренные операции для матриц:

6. Решить системы линейных уравнений:
а)  ; б)
; б)  ;
;
Основы программирования в системе Scilab
1. Условные операторы и операторы цикла
а) Условный оператор if имеет следующую структуру:
if < логическое выражение> then <инструкции>
elseif < логическое выражение> then <инструкции>,
else <инструкции>,
End
б) Цикл типа for – end:
for var = < выражение >
<инструкция 1;>
<инструкция 2;>
……………….
<инструкция т,>
End
в) Цикл типа while – end:
while < условие >
< инструкции, >
End
2. Файлы-функции
Файлы-функции играют роль подпрограмм. Имеют следующую структуру:
function [y1,…,yn]= fun (x1,…,xm)
тело функции
Endfunction
Здесь fun – имя функции, xi – входные аргументы функции, yi – выходные значения.
Нужно набрать текст в любом текстовом редакторе и сохранить в файле с именем fun. Затем следует вызвать этот файл с помощью команды exec.
Примеры.
1) if x>5 then y=8, t =6; else y=x^2, end
2) a=[];
for i=1:2
for j=1:2
a(i,j)=i+j;
end
end
3) x=1; while x<14, x=x*2,end
4) function[y]=def(x)
x=real(x)
if x>=0 then y=x*x, end
if x<0 then y=x*x*x, end
endfunction
Задачи для самостоятельного решения
1. Построить файл-функцию для вычисления факториала
2. Составить программу для вычисления значения y при заданном значении х.
а)  ;
; 
б)  ;
; 
3. C использованием одномерных массивов составить программу для решения следующих задач: дана последовательность из 15 чисел.
3.1 Подсчитать количество отрицательных элементов последовательности.
3.2 Найти сумму элементов последовательности с нечетными и сумму элементов с четными порядковыми номерами.
3.3 Найти сумму отрицательных и сумму положительных элементов последовательности.
3.4 Найти минимальный и максимальный элементы последовательности.
3.5 Вывести на экран элементы последовательности в возрастающем порядке.
3.6 Подсчитать количество элементов последовательности кратных трем.