Однофакторный дисперсионный анализ применяют в тех случаях, когда может быть указан один фактор, влияющий на конечный результат, и этот фактор может принимать конечное число значений (уровней). Типичный пример задачи однофакторного анализа - сравнение по достигаемым результатам нескольких различных способов действия, направленных на достижение одной цели, например, нескольких школьных учебников, различных доз удобрений, нескольких лекарств.
Рассмотрим применение метода на следующем примере:
Для выяснения влияния денежного стимулирования на производительность труда шести однородным группам из 5 человек были предложены задачи одинаковой трудности. Задачи предлагались испытуемому независимо от всех остальных. Группы различаются между собой величиной денежного вознаграждения за решаемую задачу. Группы упорядочены по возрастанию влияния фактора.
Исходные данные группируются в виде таблицы, в которой градации регулируемого фактора располагаются по горизонтали в верхней части таблицы, а числовые значения признака размещаются по градациям фактора.
A B C D E
рис.6
| Влияние величины вознаграждения на производительность труда | |||||
| гр.1 | гр.2 | гр.3 | гр.4 | гр.5 | |
Если регулируемый фактор (размер вознаграждения) оказывает существенное влияние на результативный признак (количество решенных задач), то это скажется на величине групповых средних, которые будут заметно отличаться друг от друга.
Нулевая гипотеза сводится к предположению, что генеральные межгрупповые средние и дисперсии равны между собой, а различия, наблюдаемые между выборочными показателями, вызваны случайными причинами, а не влиянием на признак регулируемого фактора. Нулевую гипотезу отвергают, если дисперсионное отношение Fф  Fст (критерий Фишера) для принятого уровня значимости - a.
Fст (критерий Фишера) для принятого уровня значимости - a.
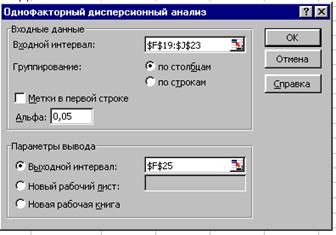 |
Для проведения однофакторного анализа введем исходные данные в таблицу в форме представленной на рисунке 6. Выполним команду Сервис/Анализ данных, в открывшемся списке выберем Однофакторный дисперсионный анализ и зададим параметры в диалоговом окне. Вид окна представлен на рисунке 7.
Рис. 7
Для ввода исходного диапазона блок данных можно выделить непосредственно в таблице. Уровень значимости задается в поле Альфа вводом значения с клавиатуры, в поле Выходной интервал указывается адрес верхней левой ячейки области размещения выходных таблиц. Выходные таблицы могут быть размещены на том же рабочем листе, на другом листе или в другом файле.
Рис.8
| ИТОГИ | ||||||
| Группы | Счет | Сумма | Среднее | Дисперсия | ||
| Столбец 1 | ||||||
| Столбец 2 | 11,8 | 9,2 | ||||
| Столбец 3 | 13,6 | 10,3 | ||||
| Столбец 4 | 15,6 | 6,3 | ||||
| Столбец 5 | 22,6 | 15,3 | ||||
| ANOVA | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 474,64 | 118,66 | 12,86985 | 2,41219E-05 | 2,866080706 | |
| Внутри групп | 184,4 | 9,22 | ||||
| Итого | 659,04 |
На рисунке 8 показан результат работы программы. В таблице ANOVA
SS -сумма квадратов,
df -число степеней свободы,
MS - средние квадраты,
F - дисперсионное отношение (отношение MS между группами к MS внутри групп). Значение F используется для проверки нулевой гипотезы.
F критическое - табличная величина, критические значения F определены для нескольких уровней значимости (0,1; 0,05; 0,01).
Из таблицы видно, что фактическое значение F, больше критического значения, поэтому гипотеза об отсутствии влияния фактора на исследуемый признак (нулевая гипотеза) должна быть отвергнута. Этот результат позволяет сделать заключение о том, что варьирование признака по группам достаточно велико, чтобы быть предметом статистического анализа.
Корреляционный анали з
Сопряженность между переменными величинами X и Y можно установить, сопоставляя значения одной из них со значениями другой. Связь между величинами может иметь однозначный, функциональный характер, когда каждому значению независимой переменной Х можно поставить в соответствие определенное значение зависимой переменной Y. Однако такого рода связи между переменными встречаются далеко не всегда. Например, зависимость между биологическими признаками, например, ростом и массой тела. Хотя между этими показателями имеется положительная связь, однако, из этого правила существуют исключения. Причина таких исключений заключается в том, что каждый биологический признак представляет собой функцию ни одного, а многих переменных. Зависимость между такими признаками носит не функциональный, а статистический характер и называется корреляционной зависимостью. Корреляционная связь между признаками может быть линейной и нелинейной, положительной и отрицательной. Значение коэффициента корреляции может находиться в пределах от -1 до +1.
Корреляционный анализ дает возможность установить, ассоциированы ли наборы данных по величине, то есть, большие значения из одного набора данных связаны с большими значениями другого набора (положительная корреляция), или, наоборот, малые значения одного набора связаны с большими значениями другого (отрицательная корреляция), или данные двух диапазонов никак не связаны (корреляция близка к нулю). При положительной связи коэффициент корреляции имеет знак “+” и находится в пределах от 0 до 1.
Для вычисления коэффициента корреляции между двумя наборами данных используется статистическая функция КОРРЕЛ или программа Корреляция, входящая в Пакет анализа.
В таблице приведены средние баллы контрольных работ по химии и биологии.
| химия | биология |
| 3,1 | 3,65 |
| 3,17 | 3,11 |
| 3,76 | 3,57 |
| 3,61 | 3,61 |
| 3,27 | 3,44 |
| 3,61 | 3,71 |
| 3,8 | 3,61 |
| 3,65 | 3,98 |
| 3,34 | 3,36 |
| 3,65 | 3,89 |
| 3,45 | 3,45 |
| 4,05 | 3,79 |
Для вычисления коэффициента корреляции вводим данные в таблицу и вызываем программу Корреляция. В диалоговом окне указываем диапазон входного интервала и адрес верхней левой ячейки выходного интервала. Значения коэффициента корреляции для приведенных данных равно 0,597688.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Какой командой открывается список программ, входящих в пакет анализа данных?
2. Какие статистические характеристики могут быть рассчитаны с помощью программы Описательная статистика?
3. Какая из программ Пакета анализа применима для оценки эффективности экспериментальной работы, проведенной в одной группе?
4. В каких случаях применим однофакторный дисперсионный анализ?
5. Какая связь между признаками называется корреляционной?
6. В каких пределах находится коэффициент корреляции при положительной связи между признаками?