Билеты по геометрии за 9 класс.
1. Треугольник однозначно можно определить по следующим тройкам основных элементов:
- a, b, γ (равенство по двум сторонам и углу лежащему между ними);
- a, β, γ (равенство по стороне и двум прилежащим углам);
- a, b, c (равенство по трём сторонам).
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
2.Свойства:
- Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектриса, медианы и высоты, проведённые из этих углов.
- Биссектриса, медиана и высота, проведенные к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.
- Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).
Признаки:
- Два угла треугольника равны.
- Высота совпадает с медианой.
- Высота совпадает с биссектрисой.
- Биссектриса совпадает с медианой.
3. Параллельные прямые в евклидовой геометрии, прямые, которые не пересекаются.
· Две прямые, параллельные третьей, параллельны.
Это свойство называется транзитивностью параллельности прямых.
· Через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
· Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
На основании этой теоремы легко обосновываются следующие свойства:
Если две параллельные прямые пересечены третьей прямой, то соответствующие и накрестлежащие углы равны.
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180°.
4. Нера́венство треуго́льника в геометрии и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение метрического пространства, нормы и т.д.; также, часто является теоремой в различных теориях.
5. Теорема о сумме углов треугольника — классическая теорема евклидовой геометрии, утверждает, что
| Сумма углов треугольника равна 180°. |
Пусть ABC' — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны прямой BC. Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD. Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Теорема доказана.
6. Серединный перпендикуляр (медиатриса) — прямая, перпендикулярная к данному отрезку и делящая его на две равные части.
Свойства
- Серединные перпендикуляры к сторонам треугольника (или другого описываемого окружностью многоугольника) пересекаются в одной точке — центре описанной окружности.
- Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
- Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Биссектриса есть геометрическое место точек, равноудаленных от сторон угла.
7. Параллелограмм (рис. 1.8)
Свойства сторон и углов: 



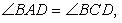


Свойства диагоналей: 


Площадь: 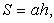
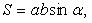


8. Ромб (рис. 1.9)
Свойства сторон и диагоналей: 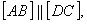

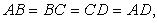


Площадь: 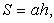


Прямоугольник (рис. 1.10)
Свойства сторон и углов: 



Свойства диагоналей: 

Площадь: 

Квадрат (рис. 1.11)
Свойства сторон и углов: 

Длина диагонали: 
Площадь: 

Трапеция (рис. 1.12)
Свойства сторон: 

Свойства средней линии: 

Площадь: 

9.
|
Доказательство:
 Пусть ABCD - данная трапеция. Проведем через вершину B и середину боковой стороны P прямую. E=ADÇ BP.
Пусть ABCD - данная трапеция. Проведем через вершину B и середину боковой стороны P прямую. E=ADÇ BP.
DPBC=DPED (по второму признаку):
1. СP=DP по построению
2. ÐBPQ=ÐEPD как вертикальные
3. ÐPCB=ÐPDE как внутренние накрест лежащие при AD||BC и секущей CD
Из DPBC=DPED ÞPB=PE, BC=ED. Значит средняя линия PQ трапеции - средняя линия DABE.
По свойству средней линии треугольника - PQ=1/2 AE=1/2(AD+BC) и PQ||AD, PQ||BC.
10. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Докозательство:
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые AA 1 | | BB 1 | | CC 1 | | DD 1 и при этом AB = CD.
- Проведём через точки A и C прямые, параллельные другой стороне угла. Получим два параллелограмма AB 2 B 1 A 1 и CD 2 D 1 C 1. Согласно свойству параллелограмма: AB 2 = A 1 B 1 и CD 2 = C 1 D 1.
- Треугольники
 и
и  равны на основании второго признака равенства треугольников:
равны на основании второго признака равенства треугольников:
AB = CD согласно условию теоремы,
 как соответственные, образовавшиеся при пересечении параллельных BB 1 и DD 1 прямой BD.
как соответственные, образовавшиеся при пересечении параллельных BB 1 и DD 1 прямой BD.
Аналогично каждый из углов  и
и 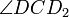 оказывается равным углу с вершиной в точке пересечения секущих.
оказывается равным углу с вершиной в точке пересечения секущих.
- AB 2 = CD 2 как соответственные элементы в равных треугольниках.
- A 1 B 1 = AB 2 = CD 2 = C 1 D 1 ■

11. Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже: #Свойства). Фигуры с одинаковой площадью называются равновеликими.

Площадь прямоугольника со сторонами a, b вычисляется по формуле S = a*b.
12.
 , так как
, так как  , то:
, то:


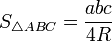

13. Формулировка:
| В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. |
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a 2 + b 2 = c 2
Доказательство через равнодополняемость
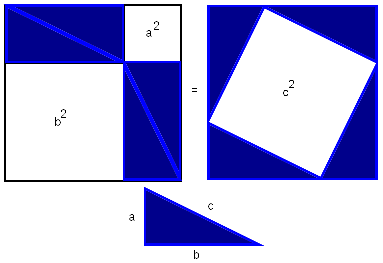
- Расположим четыре равных прямоугольных треугольника так, как показано на рисунке 1.
- Четырёхугольник со сторонами c является квадратом, так как сумма двух острых углов 90°, а развёрнутый угол — 180°.
- Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b), а с другой стороны, сумме площадей четырёх треугольников и площади внутреннего квадрата.

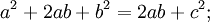

Обратная теорема Пифагора:
| Для всякой тройки положительных чисел a, b и c, такой, что a 2 + b 2 = c 2, существует прямоугольный треугольник с катетами a и b и гипотенузой c. |
14. Первый признак
| Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны. |
Второй признак
| Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны. |
Третий признак
| Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны. |
 Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Теорема. Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине. 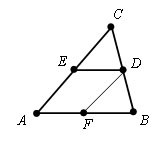 Доказательство. Пусть дан Δ ABC и его средняя линия ED. Проведем прямую параллельную стороне AB через точку D. По теореме Фалеса она пересекает отрезок AC в его середине, т.е. совпадает с DE. Значит, средняя линия параллельна AB. Проведем теперь среднюю линию DF. Она параллельна стороне AC. Четырехугольник AEDF – параллелограмм. По свойству параллелограмма ED=AF, а так как AF=FB по теореме Фалеса, то ED =? AB. Теорема доказана.
Доказательство. Пусть дан Δ ABC и его средняя линия ED. Проведем прямую параллельную стороне AB через точку D. По теореме Фалеса она пересекает отрезок AC в его середине, т.е. совпадает с DE. Значит, средняя линия параллельна AB. Проведем теперь среднюю линию DF. Она параллельна стороне AC. Четырехугольник AEDF – параллелограмм. По свойству параллелограмма ED=AF, а так как AF=FB по теореме Фалеса, то ED =? AB. Теорема доказана.