Действия со случайными величинами. Свойства математического ожидания и дисперсии
Действия с дискретными случайными величинами
Суммой двух дискретных случайных величин Х и Y называется случайная величина Z, которая принимает все возможные значения вида 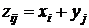 с соответствующими вероятностями
с соответствующими вероятностями  .
.
Разностью  называется случайная величина Z, принимающая все возможные значения вида
называется случайная величина Z, принимающая все возможные значения вида  с соответствующими вероятностями
с соответствующими вероятностями  .
.
Произведением  называется случайная величина Z, которая принимает все возможные значения вида
называется случайная величина Z, которая принимает все возможные значения вида  с соответствующими вероятностями
с соответствующими вероятностями  .
.
Под  понимается любое из значений случайной величины Х:
понимается любое из значений случайной величины Х:  , а под
, а под  любое из значений случайной величины Y:
любое из значений случайной величины Y: 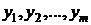 . Способ вычисления вероятности
. Способ вычисления вероятности  определяется тем, какого рода случайные величины участвуют в действии. Если эти величины независимы, т.е. вероятность того, что Х примет некоторое значение х, не зависит от того, какое значение примет Y, то
определяется тем, какого рода случайные величины участвуют в действии. Если эти величины независимы, т.е. вероятность того, что Х примет некоторое значение х, не зависит от того, какое значение примет Y, то
 , где
, где  .
.
Если величины Х и Y зависимы, то используются условные вероятности.
Выполнение действий с двумя случайными величинами удобно вести следующим образом.
Пример. Даны две независимые случайные величины Х и Y:

| – 2 | 
| ||||||||

| 0,1 | 0,2 | 0,2 | 0,3 | 0,2 | 
| 0,3 | 0,3 | 0,4 |
Найти ряд распределения случайной величины 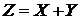 . Значения величины Z и их вероятности найдем с помощью таблицы. В клетках этой таблицы вверху слева указаны значения Z при соответствующих значениях Х и Y, внизу справа указаны их вероятности.
. Значения величины Z и их вероятности найдем с помощью таблицы. В клетках этой таблицы вверху слева указаны значения Z при соответствующих значениях Х и Y, внизу справа указаны их вероятности.
| Х | –2 | |||||||||||
| Y | 0,1 | 0,2 | 0,2 | 0,3 | 0,2 | |||||||
| 0,3 | ||||||||||||
| 0,03 | 0,06 | 0,06 | 0,09 | 0,06 | ||||||||
| 0,3 | ||||||||||||
| 0,03 | 0,06 | 0,06 | 0,09 | 0,06 | ||||||||
| 0,4 | ||||||||||||
| 0,04 | 0,08 | 0,04 | 0,12 | 0,09 | ||||||||
Выпишем ряд распределения Z:

| |||||||||||||||

| 0,03 | 0,06 | 0,06 | 0,03 | 0,09 | 0,06 | 0,06 | 0,06 | 0,04 | 0,09 | 0,08 | 0,06 | 0,08 | 0,12 | 0,06 |
Следует отметить некоторые отличия действий со случайными величинами от действий с обычными величинами, например,  . Определим
. Определим  :
:
| X | –2 | ||||||||||
| X | 0,1 | 0,2 | 0,2 | 0,3 | 0,2 | ||||||
| –2 | 0,1 | –4 | –8 | –12 | |||||||
| 0,01 | 0,02 | 0,02 | 0,03 | 0,02 | |||||||
| 0,2 | |||||||||||
| 0,02 | 0,04 | 0,04 | 0,06 | 0,04 | |||||||
| 0,2 | –4 | ||||||||||
| 0,02 | 0,04 | 0,04 | 0,06 | 0,04 | |||||||
| 0,3 | –8 | ||||||||||
| 0,03 | 0,06 | 0,06 | 0,09 | 0,06 | |||||||
| 0,2 | –12 | ||||||||||
| 0,02 | 0,04 | 0,04 | 0,06 | 0,04 |
В ряд распределения  повторяющиеся значения заносим с суммарной вероятностью
повторяющиеся значения заносим с суммарной вероятностью
| –12 | –8 | –4 | |||||||
| 0,04 | 0,06 | 0,04 | 0,36 | 0,05 | 0,12 | 0,08 | 0,09 | 0,12 | 0,04 |
Распределение же  выглядит так
выглядит так
| 0,2 | 0,3 | 0,3 | 0,2 |
Если в действии участвуют более двух случайных величин, то действие можно выполнить последовательно. Например, чтобы найти сумму  , нужно найти
, нужно найти  ,
,  ,
,  ,
,  .
.
Действия с непрерывными случайными величинами определить гораздо сложнее, кроме того, практически в опыте непрерывные случайные величины представлены набором дискретных значений, поэтому действия с непрерывными случайными величинами рассматривать не будем.
Во многих случаях вполне достаточно бывает, не выписывая подробно распределения случайной величины, полученной в результате действий с другими случайными величинами, найти ее числовые характеристики.
Свойства числовых характеристик случайной величины
Первые два свойства легко получаются из определения математического ожидания.
1. Математическое ожидание постоянной величины равно этой постоянной.
2. Постоянный множитель можно выносить за знак математического ожидания

3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий.
Возьмем для примера случайные величины X и Y, заданные следующим образом
| X: | x 1 | x 2 | Y: | y 1 | y 2 | y 3 |
| p 1 | p 2 | q 1 | q 2 | q 3 |
Используя определение суммы случайных величин и математического ожидания, можем написать
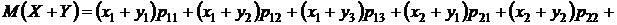



Это свойство можно распространить на сумму любого конечного числа случайных величин
 .
.
4. Математическое ожидание разности случайных величин равно разности их математических ожиданий
 .
.
5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий
 .
.
6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно 0. Используя свойства 1 и 4, получим
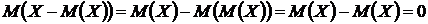 .
.
Теперь рассмотрим свойства дисперсии, предварительно вспомнив ее определение. Дисперсия случайной величины X равна математическому ожиданию квадрата отклонения X от M (X):
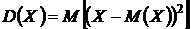 .
.
7. Дисперсия постоянной величины равна 0.
 .
.
8. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
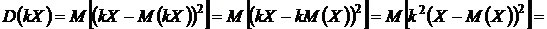
 .
.
9. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенный коэффициент ковариации.

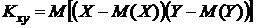 – корреляционный момент, также называемый коэффициентом ковариации, т.е. коэффициентом совместного изменения. Коэффициент ковариации можно преобразовать следующим образом:
– корреляционный момент, также называемый коэффициентом ковариации, т.е. коэффициентом совместного изменения. Коэффициент ковариации можно преобразовать следующим образом:
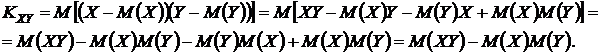
Если случайные величины Х и Y независимы, то дисперсия их суммы равна сумме дисперсий:  . Действительно, если Х и Y независимы, то и их отклонения от математических ожиданий будут независимы. Используя свойства 5 и 6,
. Действительно, если Х и Y независимы, то и их отклонения от математических ожиданий будут независимы. Используя свойства 5 и 6,
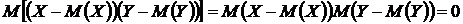 .
.
В этом случае  . Дисперсия суммы независимых случайных величин равна сумме их дисперсий
. Дисперсия суммы независимых случайных величин равна сумме их дисперсий
 .
.
10. Дисперсия разности независимых случайных величин равна сумме их дисперсий
 .
.