Методическая схема изучения параллельных и скрещивающихся прямых в пространстве

· одновременно проговорить определения и произвести построения (выполняется учителем);

· одновременно проговорить определения и показать соответствующие построения на готовом рисунке (выполняется учеником); стереть имеющийся на доске рисунок;

· одновременно проговорить определение и выполнить новый рисунок (выполняется учеником).

Методику изучения теорем и их доказательств рассмотрим на примере признака параллельности прямой и плоскости: “Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости”.

Методическая схема:

1) подвести учащихся к теореме, сформулировать ее;

2) выполнить рисунок, краткую запись теоремы;

3) сообщать общую идею теоремы;

4) привести план доказательства;

5) предоставить учащимся возможность самостоятельно осуществить док-во;

6) осуществить доказательство (ученик);

7) закрепить доказательство путем его воспроизведения;

8) применить теорему к решению задач.

Подведение учащихся к теореме: на стол положим спицу а₁, вторую спицу положим так, чтобы она была параллельна спице а₁.

Вопрос: что можно сказать о взаимном расположении спицы а и поверхности стола?

После опыта задается вопрос: Какую теорему можно сформулировать?

Идея доказательства: (после выполнения рисунка и краткой записи теоремы).

Выполним доп. построение: через параллельные прямые а и а₁ проведем плоскость a₁.

Док-во от противного:

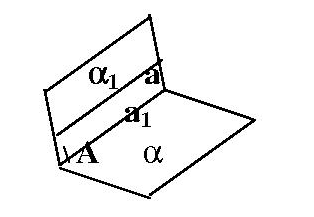
Учтем, что все общие точки плоскостей a и a₁ должны принадлежать прямой а₁.

План доказательства:

1) проводим плоскость a₁;

2) делаем допущение, что а не параллельна a;

3) рассмотрим точку А, точку пересечения прямой а и плоскости a;

4) приходим к выводу, что прямые а и а₁ пересекаются;

5) противоречие;

6) а // a.

После проведения доказательства решим следующую задачу:

Пусть SABC тетраэдр. MKP- середины ребер SA, SB, SC

Как располагаются прямые MK, KP, MP относительно ABC?

MK -средняя линия DASB => MK //AB => MK//ABC. Аналогично для др. прямых.

2. Методика изучения перпендикулярности прямых и плоскостей. Методическая схема изучения признака перпендикулярности прямой и плоскости

Содержание: определения: перпендикулярных прямых, перпендикулярных прямой и плоскости, перпендикуляра к плоскости, расстояние от точки до плоскости, наклонной, прямоугольной проекции наклонной, перпендикулярных плоскостей, теоремы о перпендикулярных прямых, признак перпендикулярности прямой и плоскости, теорем о связи между параллельностью и перпендикулярностью прямых и плоскостей в пространстве, теорема о трех перпендикулярах, теорема о перпендикулярных плоскостях.

Т.к. в учебнике Погорелова не вводится понятие о перпендикулярных скрещивающихся прямых то: пряма а, пересекающая плоскость a, называется перпендикулярной к плоскости a, если она перпендикулярнак любой прямой в плоскости a, проходящей через точку пересечения прямой а с плоскостью a.

Определения, приведенные в этой теме, относятся к генетическим (конструктивным), поэтому при их изучении используют методическую схему, определенную в “2” для параллельного проектирования. Согласно определения к плоскости проводим прямую, кот. пересекает ее в некоторой точке А. В этой плоскости найдется прямая, проходящая через точку пересечения.

Если эта прямая перпендикулярнакданной прямой, то ее называют перпендикулярной к плоскости. По рисунку куба попросить учащихся обозначить ребра куба, перпендикулярные к плоскостям AA₁BB₁, ABCD, D₁C₁CD, и назвать плоскости, которым перпендикулярны ребра C₁D₁, A₁D₁, BC.

Признак перпендикулярности:

Если прямая, пересекающая плоскость, перпендикулярна к двум прямым в этой плоскости, то она перпендикулярна к плоскости.

Сформулировать эту теорему учащиеся смогут сами, используя приведенную выше задачу (например, ребро А₁D₁ перпендикулярнок плоскости DD₁C₁ => А₁D₁^DD₁ и А₁D₁^D₁С₁ т.е. двум прямым лежащим в этой плоскости).