Лекция №2
Тема: «Внутренние усилия в поперечных сечениях стержня»
Вопросы:
Метод сечений для определения внутренних сил
Напряжения
Продольные силы и их эпюры
Определение внешних моментов и построение эпюр крутящих моментов
Метод сечений для определения внутренних сил
Как уже отмечалось, до приложения к телу нагрузки, внутри его не возникает внутренних усилий (4-е допущение). При приложении внешних сил или моментов внутри тела появляются внутренние силовые факторы. Их определяют методом сечений. Для этого в интересующем нас месте делается мысленный разрез, отбрасывается одна часть тела (обычно та, на которую действует больше сил), а ее воздействие на оставшуюся заменяется внутренними силовыми факторами, значение которых находят из уравнений статического равновесия рассматриваемой части тела.
Возможны два варианта решения задачи:
а) внешние силы и моменты находятся в одной плоскости, проходящей через центр тяжести сечения (плоская задача);
б) внешние силы и моменты не находятся в одной плоскости (пространственная задача).
Рассмотрим плоскую задачу. Пусть на тело (рис. 1) действует система сил, лежащих в одной плоскости и оно находится в статическом равновесии. Определим внутренние усилия в сечении 1-1. Отбрасываем правую часть тела, а ее воздействие на левую заменим на три силовые факторы: продольную силу N, направленную перпендикулярно плоскости сечения; поперечную силу Q, лежащую в плоскости сечения (на рисунке она несколько смещена вправо для того, чтобы она не сливалась с сечением); изгибающий момент М, плоскость действия которого перпендикулярна плоскости сечения.
|
|
Рис. 1
Для нахождения внутренних силовых факторов проведем оси координат через центр тяжести сечения OX, OY и составим уравнения статического равновесия:
; 
;
где 
и 
– соответственно проекции сил 
и 
на ось OY.
.
; 
;
где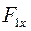 
и 
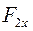– соответственно проекции сил и на ось OX.
; 
где a1 и a2 плечи сил и , т.е. кратчайшие стояния от точки 0 до направления действия сил (плечо a2 не показано, чтобы не усложнять рисунок).
Аналогично определяют усилия в сечениях 2-2, 3-3 и т.д. по всей длине тела. Определив значения N, Q и M строят эпюры (графики) каждого внутреннего усилия в отдельности. По эпюрам находят опасное сечение (сечения). Опасным считают сечение, где одно из внутренних усилий имеет максимальное значение. Это важно при расчете брусьев постоянного сечения (стержней), так как там, где внутреннее усилие максимально, возможна потеря прочности. А если прочность обеспечена в опасном сечении, то она обеспечена для всего стержня.
При плоской задаче опасных сечений может быть три. При некоторых видах нагружения два из трех внутренних усилий могут быть равны нулю, и тогда будет одно опасное сечение. Возможен также вариант, когда все внутренние усилия имеют максимум в одном сечении. Тогда тоже будет одно опасное сечение.
Рассмотрим пространственную задачу, т.е. когда внешние силы и моменты не лежат в одной плоскости (рис. 2).
Рис. 2
Внутренних усилий будет шесть: три силы и три момента, т.е. одна сила и один момент относительно каждой оси координат (две силы или два момента относительно одной оси быть не может, так как они сложатся и будет результатируюшая, т.е. одна сила или момент).
|
|
Сила, перпендикулярная сечению, называется продольной N и направлена по оси Z. Сила, лежащая в плоскости сечения, называется поперечной Q. Их будет две: вдоль осей Y и X соответственно Qy и Qx. Эти силы можно сложить по правилу параллелограмма и получить одну силу Q. Моменты Mx и My действуют перпендикулярно плоскости сечения, поэтому являются изгибающими. Момент Mz лежит в плоскости сечения и называется крутящим моментом Т.
Для пространственной задачи составляется шесть уравнений статического равновесия:
; определяем 
;
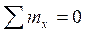; определяем 
;
; определяем 
;
; определяем 
;
; определяем 
;
; определяем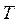 
.
Возможны следующие частные случаи возникновения внутренних усилий в сечении:
а) только продольная сила N. Это случай растяжения (сила направлена от сечения) или сжатия (сила направлена внутрь тела);
б) только поперечная сила Q.Это случай сдвига;
в) только крутящий момент Т. Это случай кручения;
г) только изгибающий момент Мх или только изгибающий момент Му. Это случай изгиба.
д) Несколько внутренних усилий, например, Мх и Му вместе. Это случай сложного сопротивления.
Напряжения
Внутренние усилия действуют не в одной какой-либо точке, а распределены по всему сечению, причем интенсивность их, т.е. отношение внутреннего усилия к площади сечения, в разных точках может быть различной. Интенсивность внутренних усилий называют также механическим напряжением или просто напряжением.
Напряжение – это внутренняя сила, приходящаяся на единицу площади в данной точке данного сечения. Размерность напряжения сила/площадь. Единица измерения – паскаль.
|
|
Паскаль величина небольшая. Его можно представить как давление 100 г воды, разлитой на 1 м2 поверхности. Прочность всех материалов измеряется в миллионах Па, поэтому применяют математическую приставку “мега”, т.е. миллион.
Рис. 3
1 МПа = 106 Па
Полное напряжение р можно разложить на две составляющие (рис. 3):
а) нормальную к плоскости сечения, называемую нормальным напряжением s;
б) лежащую в плоскости сечения, называемую касательным напряжением t.
Разложение полного напряжения на нормальное и касательное имеет определенный физический смысл. Нормальные напряжения возникают, когда частицы материала стремятся отдалится друг от друга или наоборот, сблизится. Касательные напряжения связаны со сдвигом частиц материала по плоскости рассматриваемого сечения.
Продольные силы и их эпюры
Рассмотрим случай, когда к стержню с жестко заделанным одним концом, приложены две силы, лежащие на одной линии с осью (рис. 4, а). Определим внутренние усилия и построим их эпюры.
Сечение 1-1 возьмем между точками А и В и рассмотрим нижнюю часть стержня (рис. 4, в). Поскольку силы лежат на одной линии, то задача будет плоской, а следовательно, могут возникать три внутренние усилия: продольная сила N, поперечная сила Q и изгибающий момент М, Их определим из уравнений статического равновесия, рассматриваемой части стержня:
; 
; 
Вывод: Если внешние силы действуют вдоль оси бруса, то в его поперечных сечениях возникает только одно внутреннее усилие –продольная сила N и стержень испытывает растяжение или сжатие. Очевидно, что в любом сечении от точки А до точки В будет одинаковое внутреннее усилие: N1 = 3 кН.
Сечение 2-2 возьмем между точками В и С (см. рис. 4, г). Сила приложена в точке В и она действует только выше этой точки. Продольная сила в сечении 2-2 определится из уравнения статического равновесия:
