Определение основных характеристик цифрового спектроанализатора

Курсовая работа

По дисциплине

"Радиотехнические цепи и сигналы"

Разработка цифрового спектронализатора

Расчетно-пояснительная записка

Разработал студент группы РТ-151 __________ Е.В Морозов _______

Подпись, дата Инициалы, фамилия

Руководитель

_____________________________

Подпись, дата Инициалы, фамилия

 

Члены комиссии

_____________________________

Подпись, дата Инициалы, фамилия

 

_____________________________

Подпись, дата Инициалы, фамилия

 

Нормоконтроллер

_____________________________

Подпись, дата Инициалы, фамилия

 

Защищена ________________________

Оценка ___________________________

 

 

ВОРОНЕЖ

Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный технический университет» (ФГБОУ ВО «ВГТУ»)

 

Кафедра радиотехники

Задание на Курсовую работу

по дисциплине "Радиотехнические цепи и сигналы"

Тема работы Разработка цифрового спектронализатора

Студент группы РТ-151

Морозов Евгений Владимирович

Номер варианта 21

 

Задание на проектирование. Разработать цифровой спектроанализатор для исследования сигналов с верхней граничной частотой спектра (кГц) при условии, что разброс амплитуд спектральных составляющих сигнала не превышает (дБ). Спектроанализатор должен обеспечивать разрешающую способность по частоте не хуже при продолжительности одного цикла анализа не более (мс). По результатам разработки необходимо:

1. Определить необходимый интервал дискретизации Т, размерность преобразования Фурье N, весовую функцию W(t) и коэффициент фрагментации R.

2. Подтвердить работоспособность предложенного варианта путем его моделирования.

3. Определить реально обеспечиваемую разрешающую способность по частоте.

 

Индивидуальные данные:

процессор: 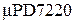, 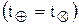=250 нс;

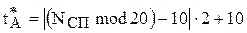=28 мс;

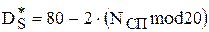=78 дБ;

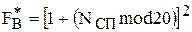=4 кГц;

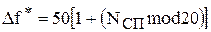=100 Гц.

Сроки выполнения этапов:

до – проведение теоретических исследований;

до – разработка моделирующей программы;

до – проведение численных расчетов и оформление курсового проекта.

 

Срок защиты курсовой работы ________________________________________

 

Руководитель _____________________________

Подпись, дата Инициалы, фамилия

 

Задание принял студент _____________________________ Е.В Морозов

Подпись, дата Инициалы, фамилия

Определение основных характеристик цифрового спектроанализатора

 

Основные теоретические сведения. При цифровом спектраль­ном анализе исходными данными служит конечная совокупность отсче­тов наблюдаемого сигнала s(t)

s_k = s(k×T),

,где k - номер отсчета (); N - число отсчетов в интервале наблю­дения Т_н (Т_н = N×T); Т £ 1 / (2F_в) - интервал дискрети­зации сигнала, F_в - высшая частота спектра сигнала. Расчет спектральной плотности вы­пол­няется по формуле дискретного преобразования Фурье

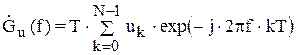, (1)

где u_k – "взвешенные" отсчеты сигнала. При отсутствии взвешивания u_k= s_k.

Определяющими являются следующие параметры цифрового спектроанализатора:

интервал дискретизации Т;

размерность преобразования Фурье N;

весовая функция W(t);

коэффициент фрагментации R.

Эти параметры полностью определяются требуемыми верхней граничной частотой спектра 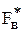, разбросом амплитуд спектральных составляющих сигнала , продолжительности одного цикла анализа и быстродействием процесора.

Найдем интервал дискретизации сигналов в цифровом спектроанализаторе. Согласно теоремы Котельникова

.

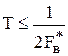В соответствии с заданием .

Примем Т=125 мкс, что соответствует частоте дискретизации 8 кГц.

Далее найдем требуемые для обеспечения заданной разрешающей способности по частоте при максимальном разбросе амплитуд время накопления и параметры оконной функции.

Подбирая форму весовой или оконной функции можно сделать боковые лепестки ее спектра сколь угодно малыми, но за это приходится платить расширением основного лепестка спектра оконной функции G_w(f).

Преобразование Фурье для произведения сигнала s(t) и про­изволь­ной функции w(t) представ­ляет собой [1,2] интег­ральную cвертку Фурье-образов сомножителей, поэтому

,

где G_w(f) - спектр весовой функции.

При спек­тральном анализе строго гармонического воздействия
s(t) = S₀ × cos(2pF₀t) вместо истинной спектральной плотности амплитуд

G_s(f) = 0.5×S₀×d(f+F₀) + 0.5×S₀×d(f-F₀)

получается кривая, описываемая функ­цией

G_u(f) = 0.5×S₀×G_w(f+F₀) + 0.5×S₀×G_w(f-F₀).

Наличие в зависимости G_u(f) боковых лепестков, величина которых определяется спектральной плотностью G_w(f) используемой весовой функ­ции w(t), существен­но ос­ложняет спектральное оценивание. Ведь если ана­лизируемый сигнал s(t) содержит на самом деле не одну, а несколько гар­моник различной амплитуды, то функция G_u(f) будет представлять собой, соответственно, сумму соответствующих откликов на каждую из имеющихся гармоник. Отличить же в результирующей зависимости G_u(f) центральные лепестки, порождаемые присутству­ющими в s(t) слабыми гармониками, от боковых лепестков, по­рождаемых более мощными спектральными составляющими, невозможно. Таким образом, значительная величина боковых лепестков спектра весовой функции при­водит на практике к ложному обнаружению спектральных составляющих анализиру­емого колебания.

В таблице 1 приведены наиболее употребительные оконные функции, применяемые при спектральном анализе.

Если разброс амплитуд гармоничес­ких составляющих сигнала не превышает

D_s = 20 lg(S_min / S_max) дБ,

где S_max - амплитуда наибольшей, а S_min - наименьшей спектральной составляющей сигнала, то используя функцию w(x) с уровнем боковых лепестков

D ≤ D_s,

и игнорируя при анализе получаемого спектра все локальные максимумы, отличающиеся от уровня глобального максимума более чем на D децибелл, можно гарантировать, что каждый из учитываемых спектральных всплесков будет соответствовать одной или нескольким маскирую­щим друг друга гармоническим составляющим сигнала, но ни один боковой лепес­ток спектра w(x) не будет ложно принят за реальную компоненту сигнала.

 

Таблица 1 - Весовые функции при спектральном оценивании и их параметры

Весовая функция во временной области w(x), |x| £ 0.5	Параметры	Уровень боковых лепестков D окна, дБ	Относительная ширина спектра окна, JD	Нормированная разрешающая способность Dfw
Прямоугольная, w(x) = 1		-13	1,64	2,0
Хеннинга, w(x) =	m = 3	-39,3	4,78	3,39
m = 4	-46,7	5,80	3,90
Хемминга, w(x) =	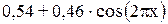-	-42,7	3,82	2,91
Кайзера-Бесселя, w(x) =	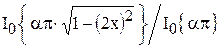a = 2,7	-62,5	5,66	3,83
a = 3,1	-72,1	6,42	4,21
a = 3,5	-81,8	7,20	4,60
Блекмана-Херриса, W(x) =	a0 = 0,35875; a1 = 0,48829 a2 = 0,14128; a3 = 0,01168	-92,0	7,90	4,95

 

Исходя из технического задания оконная функция должна иметь уровень боковых лепестков ниже минус 78 дБ. Поэтому выбираем функцию Кайзера-Бесселя с параметром a=3,5. При этом относительная ширина спектрального окна J_D=7,2 и нормированная разрешающая способность Dfw=4,60.

В выражение для окна Кайзера-Бесселя входит модифицированная функция Бесселя, имеющая вид:

I₀(z) ≈ -

 

Далее определим требуемое время накопления (наблюдения) сигнала. Эта характеристика тесно связана с разрешающей способностью. Под разрешающей способностью по частоте (РСЧ) понимают способ­ность спектроанализатора разделять (в частности, раздельно отображать) две соседние спектраль­ные составляющие анализируемо­го воздействия.

Количественной мерой разрешающей способности служит наимень­ший интервал по частоте между спектральными составляющими Df, при ко­тором число максимумов в наблюдаемом спектре однозначно определяется числом гармонических компонент в составе анализируемого колебания.

Так как близ­ким по частоте гармоническим составляющим сигнала s(t) должна соответствовать в на­б­людаемом спектре последовательность максиму­мов G_u(f), разделенных провалами, то для корректного отображения соседних гармонических компонент помимо двух отсчетов - максимумов спектра - необхо­дим по меньшей мере один отсчет, соответствующий минимуму. Поэтому теоретическим пределом разрешающей способ­ности Df при классической методи­ке спектрального оценивания служит величина Df_min = 2×f₁ [8]. С другой стороны, из-за значительной ширины главного лепестка спектра весовой функ­ции минимально необходимый для четкого разрешения частотный ин­тервал между спектральными составляющими будет равен (J_D/2 + 1)×f₁.

Таким обра­зом, спектроанализатор обеспечивает разрешающую способность по частоте

, Гц.

Отсюда требуемый частотны разнос дискретных компонентов спектра

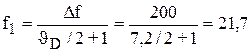Гц,

и время накопления сигнала

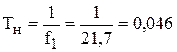с =46 мс.

Это время примерно в два раза превышает допустимое время одного цикла анализа не более =28 мс.). Поэтому для расчета спектра нужно использовать исходные данные из нескольких последовательных блоков памяти, обновляя при каждом цикле анализа лишь небольшую их часть, содержащуюся в одном очередном блоке. В результате обновленные спектральные данные будут поступать через интервал времени

T_{А парал 2} = Т ∙ N_блока.

 

Число отсчетов .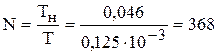

С учетом требований реализации быстрого преобразования Фурье (по степеням 2) принимаем N=512. При этом, уточненное время накопления составит

.

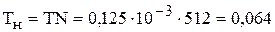Найдем время вычислений спектра. Продолжительность цикла анализа не может быть меньше времени, затрачиваемого на преобразование набора отсчетов из временной области в частотную. Кон­кретное время расчета зависит от быстродействия аппаратуры, размерности N и выбран­ного алгоритма преобразования; приближенно оно может быть оце­нено по формуле

t_расч(N) = A_r(N) × t_Å + M_r(N) × t_Ä,

где t_Å - длительность операции суммирования, t_Ä - длительность опера­ции умножения, A_r(N) и M_r(N) - общее количество вещественных сложений и умножений. Для некоторых часто используемых алгоритмов величины A_r(N) и M_r(N) приведены в таблице 2.

 

Таблица 2 - Вычислительная сложность алгоритмов быстрого преобразования Фурье типа Кули-Тьюки

Основание преобразования	Общее число умножений Mr(N)	Общее число сложений Ar(N)
N = 2m (алгоритм 1)	N×(2×log2N – 7) + 12	3×N×(log2N –1) + 4
N = 4m	9/8×N×(log2N – 2)	N/8×(25×log2N – 18)

 

Используя табличные данные и требования технического задания, находим:

t_расч = (512×(2×log₂2048– 7) + 12)× t_Å + (3×512×(log₂2048 –1) + 4) × t_Ä=

=0,0045 с=4,5 мс.

Полученное время является допустимым.

Так как Т_н > Т_расч(N), то для записи поступающих данных выделим четыре блока памяти по 128 ячеек. В этом случае время цикла анализа будет равно

T_А= Т_н/4=16 мс,

что соответствует заданным требованиям.

Таким образом, необходимый интервал дискретизации Т, размерность преобразования Фурье N, весовая функция W(t) и параметры оперативного запоминающего устройства определены. Во втором и третьем разделах проводится подтверждение принятых технических решений методом математического моделирования.

2 Расчетная (моделирующая) программа для проверки основных характеристик цифрового спектроанализатора

 

Моделирующая программа для проверки основных характеристик цифрового спектроанализатора была выполнена в среде визуального программирования MachCad. Текст программы приведен ниже.

 

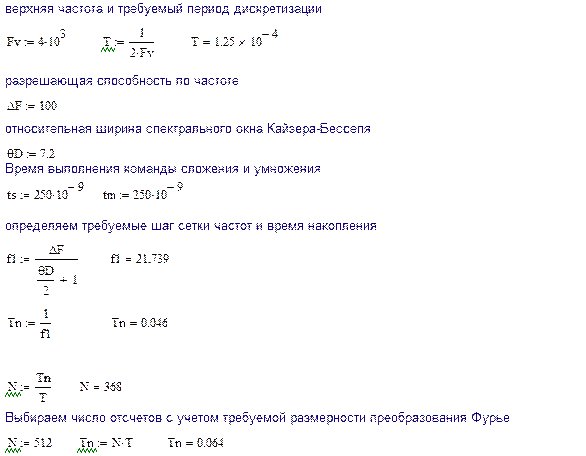
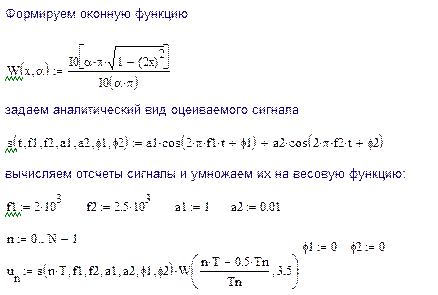
Программа построена следующим образом. В начале задается верхняя частота дискретизации и вычисляется период дискретизации.

Требуемое время накопления вычисляется с учетом определенной в разделе 1 величины нормированной ширины окна и требований по разрешающей способности. Полученной значение и время накопления уточняются с учетом того, что число отсчетов в выборке должно соответствовать значению .

Оконная функция Кайзера-Бесселя задается с использованием встроенных в систему MathCad функций Бесселя первого рода нулевого порядка.

Сигнал задается в виде двух гармонических составляющих с различными частотами, начальными фазами и амплитудами.

Для получения массива отсчетов сигнала значения сигнала в заданный момент времени умножаются на величину оконной функции.

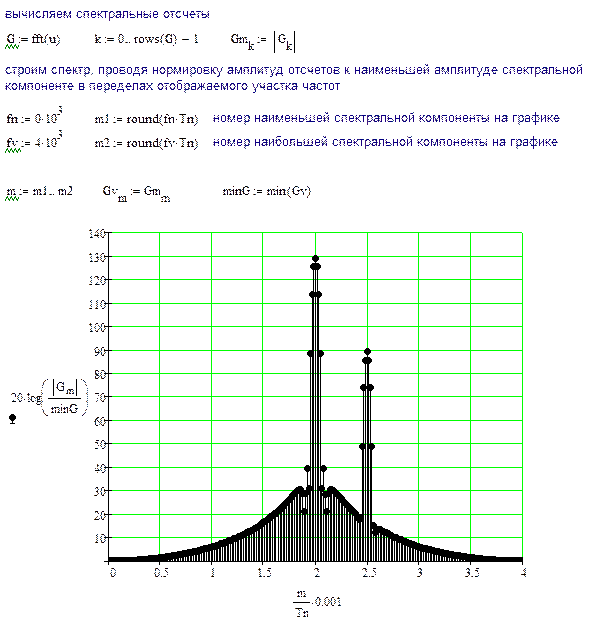
Спектр сигнала вычисляется путем быстрого преобразования Фурье с использованием стандартной функции системы MathCad fft(u), где u – массив отсчетов сигнала. Функция выдает массив комплексных спектральных компонент, поэтому при выборе спектра на график, то есть, получения спектрограммы, используются операции взятия модуля.

Спектральные отсчеты выводятся в нормированном относительно амплитуды наименьшей спектральной компоненты в пределах отображаемого участка частот виде.

Результаты моделирования при приведенных на листинге исходных данных свидетельствуют о правильности разработанной программы. В частности:

различия амплитуд сигналов адекватно различию амплитуд соответствующих спектральных компонент;

уровень боковых лепестков спектра для сигнала с большей амплитудой составляет около минус 81 дБ, что точно соответствует заданной оконной функции.