Лекция №23
Тема: «УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ»
Вопросы:
Понятие об устойчивости и критической силе
Формула Эйлера для критической силы
Пределы применимости формулы Эйлера. Формула Ясинского
Рациональные формы сечений сжатых стержней
Понятие об устойчивости и критической силе
Несущая способность сжатого стержня может оказаться исчерпанной вследствие потери устойчивости, т.е. в результате выпучивания, которое происходит раньше, чем стержень выйдет из строя непосредственно от сжатия.
При малой сжимающей силе, меньшей некоторого критического значения  , сжатый стержень находится в устойчивой форме равновесия. Если его вывести из состояния равновесия незначительной горизонтальной силой, а затем эту силу убрать, то он распрямится.
, сжатый стержень находится в устойчивой форме равновесия. Если его вывести из состояния равновесия незначительной горизонтальной силой, а затем эту силу убрать, то он распрямится.
Вторая форма равновесия соответствует случаю, когда 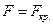 .
.
При  прямолинейная форма сжатого стержня неустойчива и если вывести его из состояния равновесия, а затем убрать боковую нагрузку, то он полностью не распрямится, т.е. у него будет криволинейная форма равновесия. Такой стержень теряет устойчивость.
прямолинейная форма сжатого стержня неустойчива и если вывести его из состояния равновесия, а затем убрать боковую нагрузку, то он полностью не распрямится, т.е. у него будет криволинейная форма равновесия. Такой стержень теряет устойчивость.
Потеря устойчивости весьма опасна с точки зрения прочности стержня и всей конструкции в целом. Незначительные повышения нагрузки вызывают значительные перемещения точек, т.е. изгиб стержня. В результате возникает изгибающий момент и связанные с ним нормальные напряжения. Это может привести к дальнейшему изгибу и разрушению стержня. Изгиб стержня от сжимающей силы называется продольным изгибом. Продольный изгиб может уменьшать несущую способность стержня в десятки раз.
Появление продольного изгиба опасно тем, что при нем происходит очень сильное нарастание прогибов при малом возрастании сжимающей силы. Прогибы и нагрузки связаны между собой нелинейной зависимостью. Быстрое нарастание прогибов вызывает быстрое нарастание напряжений от изгиба, которые в свою очередь приводят к ускорению деформаций и часто к разрушению стержня.
Для тонких (гибких) стержней потеря устойчивости часто наступает при сравнительно небольших сжимающих напряжениях, не являющихся опасными с точки зрения прочности самого материала.
Критическая сила – это наименьшее значение сжимающей силы, при которой стержень теряет устойчивую форму равновесия.
По определению Эйлера, критической силой называется сила, требующаяся для самого малого наклонения колонны.
Потеря устойчивости зачастую является главной причиной катастроф и аварий конструкций.
Формула Эйлера для критической силы
Рассмотрим сжатый стержень в критическом состоянии, т.е. когда он слегка прогнулся (см. рис. 1). В произвольном сечении взятом на расстоянии z от левого конца стержня, изгибающий момент от критической силы  равен:
равен:
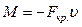 ,
,
где 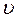 – прогиб стержня.
– прогиб стержня.
Знак «минус» взят потому, что стержень изгибается концами вниз. Если бы стержень прогнулся дугой вниз, то момент был бы положительным, но прогиб 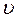 – отрицательный, и произведение
– отрицательный, и произведение 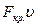 было бы, все равно, со знаком «минус».
было бы, все равно, со знаком «минус».

Рис. 1
Согласно формуле  запишем дифференциальное уравнение изогнутой оси стержня:
запишем дифференциальное уравнение изогнутой оси стержня:
 (1)
(1)
При сжатии стержня вдоль оси, он всегда изгибается относительно той оси, момент инерции относительно которой минимальный. В этом можно убедиться, сжимая линейку. Поэтому в формуле (1) берем минимальный осевой момент инерции сечения. Преобразуем уравнение (1):
 ;
;
Обозначив:
 (2)
(2)
получим:
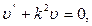 (3)
(3)
Это линейное дифференциальное уравнение второго порядка. Его решение имеет вид:
 (4)
(4)
Для определения произвольных постоянных А и В используем граничные условия.
При z=0; у=0;


Уравнение примет вид:
 . (5)
. (5)
Как видно из уравнения (5), стержень изогнется по синусоиде.
Второе граничное условие:
При z= l; у=0;

Это условие выполняется в двух случаях:
1)  2)
2) 
Первый случай отбрасываем, так как при нем прогибы всех точек равны нулю, т.е. стержень остается прямым.
При втором случае:

Возьмем общий случай:

Возведем в квадрат обе части уравнения:

Вместо  подставим его значение из формулы (2):
подставим его значение из формулы (2):

или

Принимая  ,
,  и т.д., получим последовательный ряд значений
и т.д., получим последовательный ряд значений  , которым соответствуют различные искривленные формы равновесия стержня. С точки зрения расчета на устойчивость нас интересует лишь наименьшее значение критической силы, так как уже при этом значении силы стержень теряет устойчивость. Поэтому
, которым соответствуют различные искривленные формы равновесия стержня. С точки зрения расчета на устойчивость нас интересует лишь наименьшее значение критической силы, так как уже при этом значении силы стержень теряет устойчивость. Поэтому  и формула принимает вид:
и формула принимает вид:
 (6)
(6)
Критическая сила зависит от способа закрепления концов стержня, поэтому вводится коэффициент  – коэффициент приведенной длины (не путать с коэффициентом поперечной деформации). В общем случае формула Эйлера примет вид:
– коэффициент приведенной длины (не путать с коэффициентом поперечной деформации). В общем случае формула Эйлера примет вид:
 (7)
(7)
Значения коэффициента  даны на рис. 2
даны на рис. 2

Рис. 2