(Глава 5. Дифференциальное исчисление функции одной независимой переменной)
ЗАДАНИЕ 1. Найти производные функций.
№1. а) 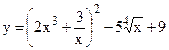 ; б)
; б)  ;
;
в) 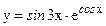 ; г)
; г)  .
.
№2. а) 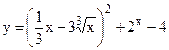 ; б)
; б) 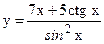 ;
;
в) 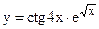 ; г)
; г) 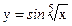 .
.
№3. а) 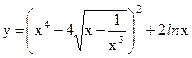 ; б)
; б) 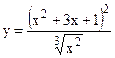 ;
;
в) 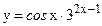 ; г)
; г)  .
.
№4. а) 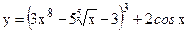 ; б)
; б)  ;
;
в) 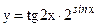 ; г)
; г)  .
.
№5. а) 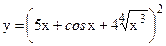 ; б)
; б) 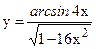 ;
;
в) 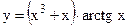 ; г)
; г) 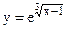 .
.
№6. а) 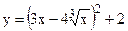 ; б)
; б) 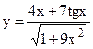 ;
;
в) 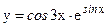 ; г)
; г) 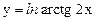 .
.
№7. а)  ; б)
; б)  ;
;
в) 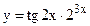 ; г)
; г) 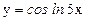 .
.
№8. а) 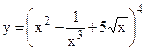 ; б)
; б)  ;
;
в) 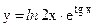 ; г)
; г)  .
.
№9. а) 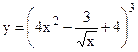 ; б)
; б) 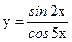 ;
;
в)  ; г)
; г) 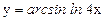 .
.
№10. а) 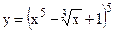 ; б)
; б) 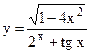 ;
;
в)  ; г)
; г) 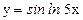 .
.
№11. а) 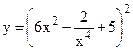 ; б)
; б)  ;
;
в) 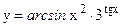 ; г)
; г)  .
.
№12. а)  ; б)
; б) 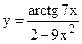 ;
;
в) 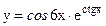 ; г)
; г)  .
.
№13. а) 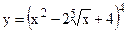 ; б)
; б) 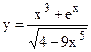 ;
;
в)  ; г)
; г) 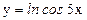 .
.
№14. а) 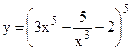 ; б)
; б) 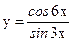 ;
;
в) 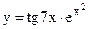 ; г)
; г) 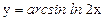 .
.
№15. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
№16. а)  ; б)
; б) 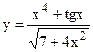 ;
;
в)  ; г)
; г)  .
.
№17. а) 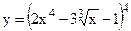 ; б)
; б) 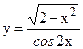 ;
;
в) 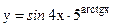 ; г)
; г)  .
.
№18. а) 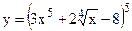 ; б)
; б)  ;
;
в)  ; г)
; г) 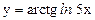 .
.
№19. а) 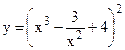 ; б)
; б) 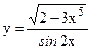 ;
;
в) 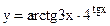 ; г)
; г) 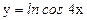 .
.
№20. а)  ; б)
; б) 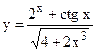 ;
;
в)  ; г)
; г) 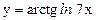 .
.
№21. а) 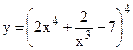 ; б)
; б) 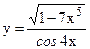 ;
;
в) 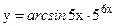 ; г)
; г) 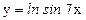 .
.
№22. а) 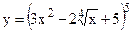 ; б)
; б) 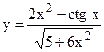 ;
;
в) 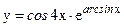 ; г)
; г) 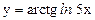 .
.
№23. а)  ; б)
; б) 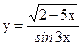 ;
;
в)  ; г)
; г) 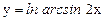 .
.
№24. а)  ; б)
; б)  ;
;
в) 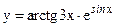 ; г)
; г)  .
.
№25. а)  ; б)
; б)  ;
;
в) 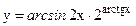 ; г)
; г) 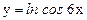 .
.
№26. а) 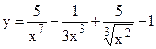 ; б)
; б) 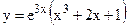 ;
;
в)  ; г)
; г) 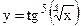 .
.
№27. а) 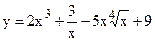 ; б)
; б) 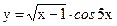 ;
;
в) 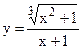 ; г)
; г) 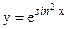 .
.
№28. а) 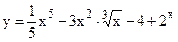 ; б)
; б)  ;
;
в) 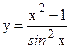 ; г)
; г) 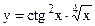 .
.
№29. а) 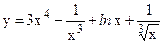 ; б)
; б) 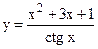 ;
;
в) 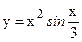 ; г)
; г) 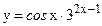 .
.
№30. а) 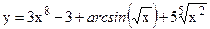 ; б)
; б) 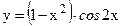 ;
;
в) 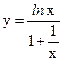 ; г)
; г) 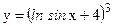 .
.
ЗАДАНИЕ 2. Найти производную 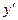 от заданной функции у.
от заданной функции у.
№1. 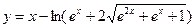
№2. 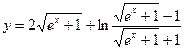
№3. 
№4. 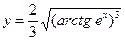
№5. 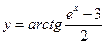
№6. 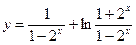
№7. 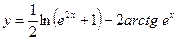
№8. 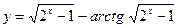
№9. 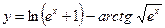
№10. 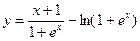
№11. 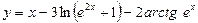
№12. 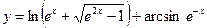
№13. 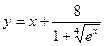
№14. 
№15. 
№16. 
№17. 
№18. 
№19. 
№20. 
№21. 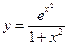
№22. 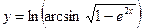
№23. 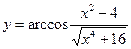
№24. 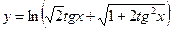
№25. 
№26. 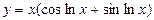
№27. 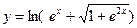
№28. 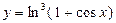
№29. 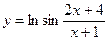
№30. 
№31. 
№32. 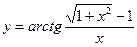
ЗАДАНИЕ 3. Найти дифференциал dy.
№1. 
№2. 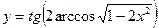
№3. 
№4. 
№5. 
№6. 
№7. 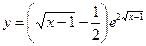
№8. 
№9. 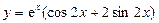
№10. 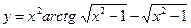
№11. 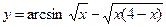
№12. 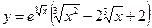
№13. 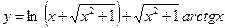
№14. 
№15. 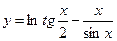
№16. 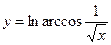
№17. 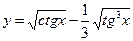
№18. 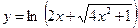
№19. 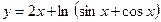
№20. 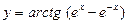
№21. 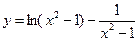
№22. 
№23. 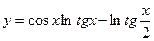
№24. 
№25. 
№26. 
№27. 
№28. 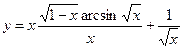
№29. 
№30. 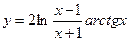
№31. 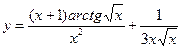
№32. 
ЗАДАНИЕ 4. Найти производную второго порядка.
№1. 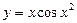
№2. 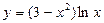
№3. 
№4. 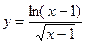
№5. 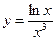
№6. 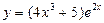
№7. 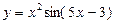
№8. 
№9. 
№10. 
№11. 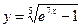
№12. 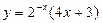
№13. 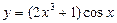
№14. 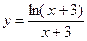
№15. 
№16. 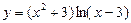
№17. 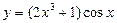
№18. 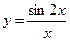
№19. 
№20. 
№21. 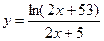
№22. 
№23. 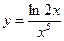
№24. 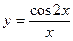
№25. 
№26. 
№27. 
№28. 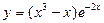
№29. 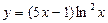
№30. 
№31. 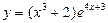
№32. 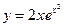
ЗАДАНИЕ 5. Найти пределы с помощью правила Лопиталя.
№1. 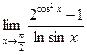
№2. 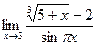
№3. 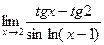
№4. 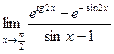
№5. 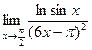
№6. 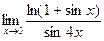
№7. 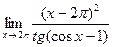
№8. 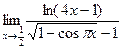
№9. 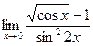
№10. 
№11. 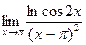
№12. 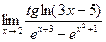
№13. 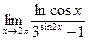
№14. 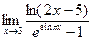
№15. 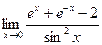
№16. 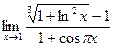
№17. 
№18. 
№19. 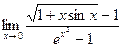
№20. 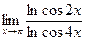
№21. 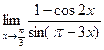
№22. 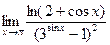
№23. 
№24. 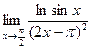
№25. 
№26. 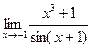
№27. 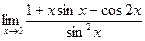
№28. 
№29. 
№30. 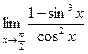
№31. 
ЗАДАНИЕ 6. Провести полное исследование функции и построить ее график.
№1. 
№2. 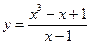
№3. 
№4. 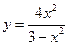
№5. 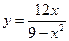
№6. 
№7. 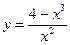
№8. 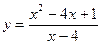
№9. 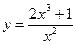
№10. 
№11. 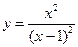
№12. 
№13. 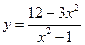
№14. 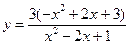
№15. 
№16. 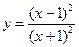
№17. 
№18. 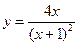
№19. 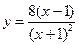
№20. 
№21. 
№22. 
№23. 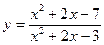
№24. 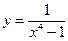
№25. 
№26. 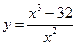
№27. 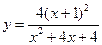
№28. 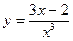
№29. 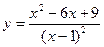
№30. 
№31. 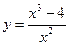
№32. 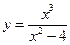
ЗАДАНИЕ 7. Провести полное исследование функции и построить ее график.
№1. 
№2. 
№3. 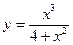
№4. 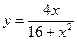
№5. 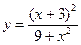
№6. 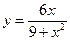
№7. 
№8. 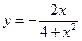
№9. 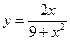
№10. 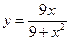
№11. 
№12. 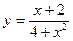
№13. 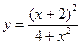
№14. 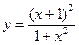
№15. 
№16. 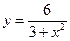
№17. 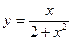
№18. 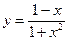
№19. 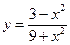
№20. 
№21. 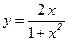
№22. 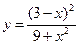
№23. 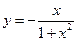
№24. 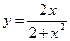
№25. 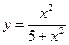
№26. 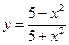
№27. 
№28. 
№29. 
№30. 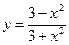
№31. 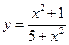
№32. 
Индивидуальные задания № 6
(Глава 6. Дифференциальное исчисление функций нескольких переменных)
ЗАДАНИЕ 1. Найти все частные производные первого порядка от данной функции.
№1. 
№2. 
№3. 
№4. 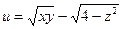
№5. 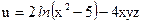
№6. 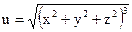
№7. 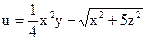
№8. 
№9. 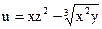
№10. 
№11. 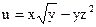
№12. 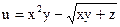
№13. 
№14. 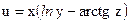
№15. 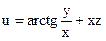
№16. 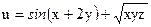
№17. 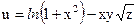
№18. 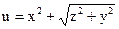
№19. 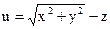
№20. 
№21. 
№22. 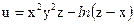
№23. 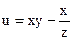
№24. 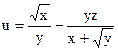
№25. 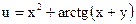
№26. 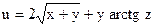
№27. 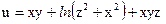
№28. 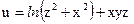
№29. 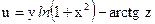
№30. 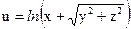
№31. 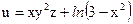
№32. 
ЗАДАНИЕ 2. Найти все частные производные первого и второго порядков от данной функции.
№1. z = xy2 – x2y
№2. z = cos x ·cos y
№3. z = xy + cos(x + y)
№4. z = xy – cos(x + y)
№5. z = x2y + xy2
№6. z = 2xy + cos(3x + y)
№7. z = xy – sin(x + y)
№8. z = y lnx
№9. z = xy3 – x3y
№10. z = x lny
№11. z = xy3 + x3y
№12. z = x sin xy
№13. z = x2y3
№14. z = y sin xy
№15. z = sin x ·cos y
№16. z = x exy
№17. z = sin x ·sin y
№18. z = y exy
№19. z = sin y ·cos x
№20. z = x ·cos y
№21. z = y ·cos xy
№22. z = x3y3 + x3 + y3
№23. z = exy
№24. z = x2y2 + x2 + y2
№25. z = x cos(x + 2y)
№26. z = 2x+y
№27. z = y cos(2x + y)
№28. z = 3x – y
№29. z = x sin(x – 2y)
№30. z = ex – 2y
№31. z = y cos(x – 2y)
№32. z = e2x – y
ЗАДАНИЕ 3. Найти полный дифференциал функции u в точке М0.
№1.  , М0(1,2,1)
, М0(1,2,1)
№2.  , М0(2,2,1)
, М0(2,2,1)
№3. u = x2yz3, М0(-1,2,1)
№4.  , М0(-1,-2,-1)
, М0(-1,-2,-1)
№5. 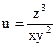 , М0(-1,-2,1)
, М0(-1,-2,1)
№6. 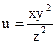 , М0(1,2,-1)
, М0(1,2,-1)
№7. 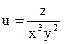 , М0(1,1,-2)
, М0(1,1,-2)
№8. 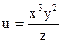 , М0(-1,2,-1)
, М0(-1,2,-1)
№9. 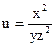 , М0(2,-1,-1)
, М0(2,-1,-1)
№10.  , М0(1,-2,1)
, М0(1,-2,1)
№11. 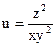 , М0(2,1,1)
, М0(2,1,1)
№12.  , М0(1,-2,-1)
, М0(1,-2,-1)
№13. u = xy2z2, М0(1,1,2)
№14. u = x2yz3, М0(2,-1,1)
№15. 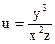 , М0(-1,1,2)
, М0(-1,1,2)
№16. 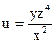 , М0(2,1,-1)
, М0(2,1,-1)
№17. u = x2y2z, М0(1,-1,2)
№18.  , М0(-2,-1,1)
, М0(-2,-1,1)
№19.  , М0(1,1,-2)
, М0(1,1,-2)
№20. 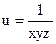 , М0(2,-1,-1)
, М0(2,-1,-1)
№21. 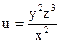 , М0(-1,-1,2)
, М0(-1,-1,2)
№22. 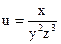 , М0(-2,1,-1)
, М0(-2,1,-1)
№23. 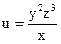 , М0(1,-1,-2)
, М0(1,-1,-2)
№24. u = x2yz, М0(-2,-1,-1)
№25.  , М0(-1,1,-2)
, М0(-1,1,-2)
№26.  , М0(2,2,1)
, М0(2,2,1)
№27. 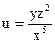 , М0(-1,-1,-2)
, М0(-1,-1,-2)
№28. 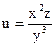 , М0(2,2,-1)
, М0(2,2,-1)
№29. 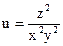 , М0(2,1,1)
, М0(2,1,1)
№30.  , М0(-2,2,-1)
, М0(-2,2,-1)
№31.  , М0(-2,1,1)
, М0(-2,1,1)
№32. 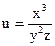 , М0(2,-2,1)
, М0(2,-2,1)
ЗАДАНИЕ 4. Найти частные производные указанного порядка от данных функций.
№1. z = x ln(x + y), 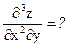
№2.  ,
, 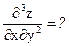
№3. z = x3siny + y3cosx, 
№4. 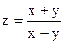 ,
, 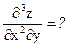
№5. z = x y ex + y, 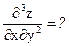
№6. z = cos(x2 + y2), 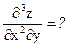
№7. z = (x2 + y2) ex + y, 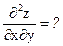
№8. z = ln tg(x + y), 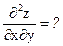
№9. z = (x + y2), 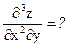
№10. z = x2ln(x + y), 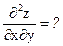
№11. 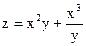 ,
, 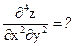
№12. z = y ln(xy), 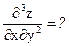
№13. z = sin(x2 + y2), 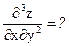
№14. 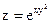 ,
, 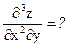
№15. 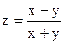 ,
, 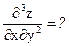
№16. z = y3sinx + x3cosy, 
№17. z = ln(x2 + y), 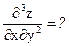
№18.  ,
, 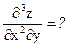
№19. 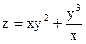 ,
, 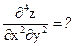
№20. 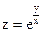 ,
, 
№21. z = y2ln(x + y), 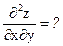
№22.  ,
, 
№23.  ,
, 
№24. 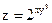 ,
, 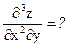
№25.  ,
, 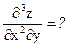
№26. 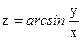 ,
, 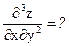
№27. 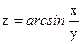 ,
, 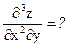
№28.  ,
, 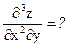
№29.  ,
, 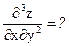
№30. z = xy cos(x – y), 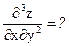
№31. z = xy cos(x + y), 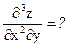
№32. z = xy sin(x + y), 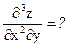
ЗАДАНИЕ 5. Исследовать функцию на экстремум.
№1. z = x2 – 2xy + 2y2 – 4x – 6y + 3
№2. z = 10 + 2xy – x2
№3. z = 2xy – 3x2 – 3y2 + 4x + 4y
№4. z = 4x + 2y + 4x2 + y2 + 6
№5. z = 4x2 + 9y2 – 4x – 6y + 3
№6. z = 2x2 – 4xy + 5y2 – 8x + 6
№7. z = 4xy – 3x2 – 12y2 + 4x + 8y – 5
№8. z = 5x2 + 8xy + 5y2 – 18x – 18y
№9. z = 5x2 – 3xy + y2 + 4
№10. z = 2x2 + y2 – xy + 3x – 2
№11. z = 3x2 – y2 + 8xy + 4y – 5
№12. z = x2 + 4y2 + 2x + 4y + 6
№13. z = 2x2 – 3y2 – xy + 5x + y
№14. z = 5x2 – 4xy + 2y2 – 8x + 6
№15. z = 3x2 + 3y2 – 2xy – 4x – 4y – 4
№16. z = 5x2 – 8xy + 5y2 – 18x + 18y
№17. z = 2x2 – 2xy + 2y2 + 2x – 6y
№18. z = x2 – xy + 2y2 + 3x – 2
№19. z = 3 + 4x + 6y – 4x2 – 9y2
№20. z = x2 + y2 – 2y + 5
№21. z = 9x2 + 4y2 – 6x – 4y + 3
№22. z = x2 – xy + y2 – 2x + y
№23. z = 4xy – 12x2 – 3y2 + 8x + 4y
№24. z = x2 – 2xy + y2 + 2x – 2y
№25. z = 3x2 + 12y2 – 4xy – 4x + 8y – 5
№26. z = 8x2 – 3xy – 3y2 – y + x
№27. z = x2 – 3xy + 5y2 + 4
№28. z = 2x2 + xy + 5x + y2
№29. z = 3xy – 5x2 – y2 – 4
№30. z = y2 – xy + 8x
№31. z = x2 – 2xy – 10
№32. z = 3x2 – 2xy + 2y2 – 10
Индивидуальные задания № 7
(Глава 7. Интегральное исчисление)
ЗАДАНИЕ 1. Вычислить указанные неопределенные интегралы.
№1. а) 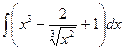 ; б)
; б) 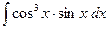 ; в)
; в)  .
.
№2. а) 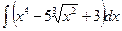 ; б)
; б) 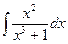 ; в)
; в)  .
.
№3. а) 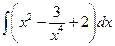 ; б)
; б) 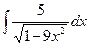 ; в)
; в)  .
.
№4. а) 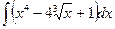 ; б)
; б)  ; в)
; в) 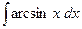 .
.
№5. а) 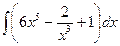 ; б)
; б) 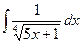 ; в)
; в)  .
.
№6. а) 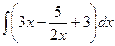 ; б)
; б) 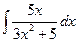 ; в)
; в) 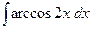 .
.
№7. а)  ; б)
; б) 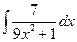 ; в)
; в) 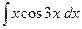 .
.
№8. а)  ; б)
; б) 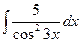 ; в)
; в) 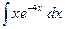 .
.
№9. а) 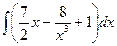 ; б)
; б) 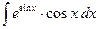 ; в)
; в) 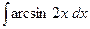 .
.
№10. а) 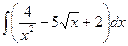 ; б)
; б) 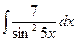 ; в)
; в) 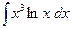 .
.
№11. а)  ; б)
; б) 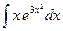 ; в)
; в) 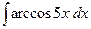 .
.
№12. а)  ; б)
; б) 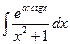 ; в)
; в) 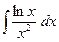 .
.
№13. а)  ; б)
; б) 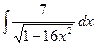 ; в)
; в) 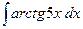 .
.
№14. а)  ; б)
; б) 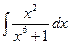 ; в)
; в) 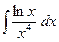 .
.
№15. а) 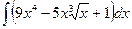 ; б)
; б) 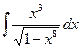 ; в)
; в)  .
.
№16. а)  ; б)
; б) 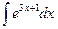 ; в)
; в)  .
.
№17. а)  ; б)
; б) 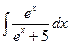 ; в)
; в) 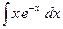 .
.
№18. а)  ; б)
; б) 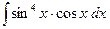 ; в)
; в) 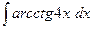 .
.
№19. а) 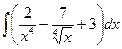 ; б)
; б) 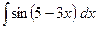 ; в)
; в)  .
.
№20. а) 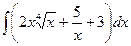 ; б)
; б) 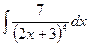 ; в)
; в)  .
.
№21. а) 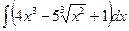 ; б)
; б) 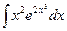 ; в)
; в) 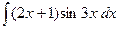 .
.
№22. а) 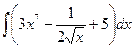 ; б)
; б) 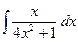 ; в)
; в) 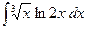 .
.
№23. а) 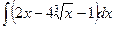 ; б)
; б) 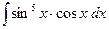 ; в)
; в)  .
.
№24. а) 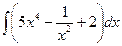 ; б)
; б) 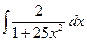 ; в)
; в) 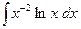 .
.
№25. а)  ; б)
; б) 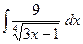 ; в)
; в)  .
.
№26. а)  ; б)
; б)  ; в)
; в)  .
.
№27. а) 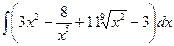 ; б)
; б) 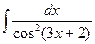 ; в)
; в) 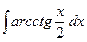 .
.
№28. а)  ; б)
; б) 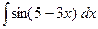 ; в)
; в) 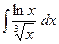 .
.
№29. а) 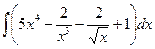 ; б)
; б) 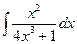 ; в)
; в) 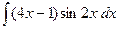 .
.
№30. а) 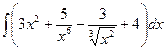 ; б)
; б)  ; в)
; в)  .
.
ЗАДАНИЕ 2. Вычислить площадь фигуры, ограниченной линиями  и
и 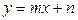 (параметры
(параметры 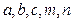 заданы в таблице). Сделать чертеж.
заданы в таблице). Сделать чертеж.
| № вар-та | <
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-10-25 Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Читайте также:
Деталирование сборочного чертежа
Когда производственнику особенно важно наличие гибких производственных мощностей?
Собственные движения и пространственные скорости звезд