Определение термодинамической возможности протекания электрохимической коррозии металлов в коррозионных средах. Написание уравнений процессов электрохимической коррозии металлов. Расчет количества металла, разрушенного коррозией, по законам Фарадея и закону эквивалентов.
Пример 1. Электрохимическая коррозия металла при контакте с воздухом.
Определите, возможна ли электрохимическая коррозия никеля (Ni) в водном растворе при рН= 6 и 298 К при контакте с воздухом. Напишите уравнения реакций анодного и катодного процессов. При каких значениях рН возможна коррозия с выделением водорода?
Решение. Энергия Гиббса процесса электрохимической коррозии непосредственно связана с ЭДС коррозионного гальванического элемента:
.
ЭДС коррозионного гальванического элемента равна разности равновесных потенциалов металла и окислителя:
>0.
Поэтому электрохимическая коррозия возможна, если 
или
.
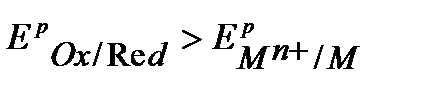В расчетах будем использовать значение стандартных потенциалов металлов. Стандартный электродный потенциал никеля: 
= –0,25В. (Приложение 6 [1]).
Равновесные потенциалы восстановления окислителей (Н+, О2) рассчитываются по уравнению Нернста:
.
Определим равновесные потенциалы вероятных окислителей (Н+ и О2) при температуре 25°С,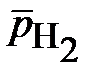 
= 1, 
= 0,21 (процентное содержание кислорода в воздухе 21%):
= –0,059×рН = –0,059×6 = –0,354 В.
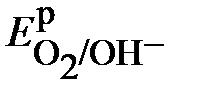= 1,227 – 0,059×рН +0,015ּlg0,21 = 1,227 – 0,059×6 – 0,01 =0,873 В.
Рассчитаем ЭДС предполагаемых коррозионных элементов:
= - = –0,354 В – (–0,25 В) = –0,104В < 0 – коррозия с выделением водорода невозможна.
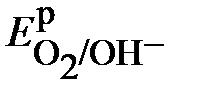- = 0,873 В – (–0,25 В) = 1,123 В > 0 – коррозия с поглощением кислорода возможна.
Уравнения реакций анодного и катодного процессов:
|
|
А: Ni ® Ni2+ + 2е
К: О2 + 4Н+ + 4е ® 2Н2О.
Для выяснения диапазона значений рН, при которых возможна коррозия никеля с водородной деполяризацией, решим неравенство:
- > 0.
После подстановки значений электродных потенциалов, получим:
–0,059×рН – (–0,25) > 0.
Откуда следует, что при значениях рН < 0,25/0,059 < 4,24 может идти процесс коррозии никеля с выделением водорода.
Пример 2. Оценкавозможности электрохимической коррозии металла в деаэрированном растворе.
Определите, будет ли корродировать медь (Сu) при 298 К в деаэрированном (без содержания кислорода) кислом растворе СuSО4 (рН=0) с выделением водорода при его относительном давлении 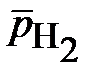= 10.
Решение. Сравним стандартный потенциал металла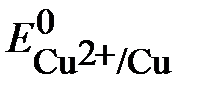 
с равновесным потенциалом окислителя .
Стандартный потенциал меди составляет 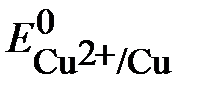= +0,337В, (Приложение 6 [1];
потенциал водорода рассчитываем по уравнению Нернста:
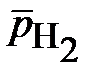= –0,0295×lg – 0,059×рН = – 0,0295×lg 
– 0,059×0 = – 0,0295В.
ЭДС коррозионного ГЭ:
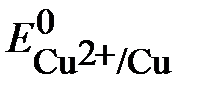- = - 0,0295 – 0,337 < 0 – коррозия протекать не будет.
Пример 3. Электрохимическая коррозия при контакте гальванической пары с коррозионной средой.
Имеется спай олова (Sn) с серебром (Ag). Определите возможность коррозии при эксплуатации изделия в щелочной среде (рН = 9) при контакте с кислородом (
) при 298 К. Напишите уравнения возможных коррозионных процессов.
Решение. В металлической конструкции, состоящий из разных металлов, корродировать может только металл с самым отрицательным значением потенциала.
По табл. (Приложение 6 [1]) определим стандартные электродные потенциалы металлов:
B, 
B,
|
|
т.к. 
, то в образующейся гальванической паре анодом будет олово, а катодом – серебро.
По уравнению Нернста определим равновесные потенциалы вероятных окислителей (Н+ и О2):
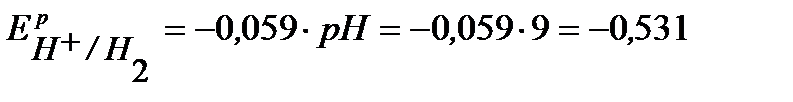B,
B.
Поскольку 
< 
< 
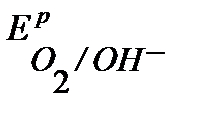, то возможной будет только коррозия олова под действием кислорода:
A– : Sn → Sn2+ + 2e.
K+ : O2 + 2H2O + 4e → 4OH–.
Пример 4. Расчет массы металла и окислителя. Расчет коррозионного тока.
При коррозии железного изделия с поглощением кислорода за 3 мин образовалось 0,125г Fe(OH)2. Вычислите объем кислорода, израсходованного на коррозию железа, силу коррозионного тока и массу металла, разрушенного коррозией.
Решение. Рассчитаем количество моль-эквивалентов образовавшегося Fe(OH)2:
моль-экв,
где молярная масса эквивалента Fe(OH)2 M Э,Fe(OH)2 = 90/2=45 г/моль.
Поскольку все вещества взаимодействуют в эквивалентных количествах, то разрушилось 2,8.10-3 моль-эквивалентов Fe и израсходовалось столько же моль-эквивалентов O2.
моль-экв.
Тогда объем кислорода (н.у.), израсходованного на коррозию железа:
мл,
где молярный объем эквивалента кислорода (н.у.) 
= 22,4/4 =5,6 л/моль.
По закону Фарадея рассчитаем силу коррозионного тока:
А.
Определим массу прокорродировавшего железа:
г,
где молярная масса эквивалента Fe(II) M Э,Fe = 56/2=28 г/моль.
Пример 5. Оценкавозможности электрохимической коррозии металла в заданном растворе электролита.
Определите возможность электрохимической коррозии стального изделия (железа) в 0,1 М растворе FеСl2, комнатной температуре (Т = 298К) при следующих относительных парциальных давлениях водорода и кислорода: 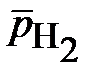= 0,1; = 0,9.
|
|
Решение. Оценим водородный показатель коррозионной среды.
Cоль FеСl2, образованная слабым основанием Fe(OH)2 и сильной кислотой HCl, подвергается гидролизу. Учитывая 1 ступень гидролиза:
Fе2+ + Н2О ↔ FеОН+ + Н+ .
Как видно из реакции, для данного раствора рН < 7, то есть коррозия идет в подкисленной среде.
Рассчитаем pH раствора, принимая активность ионов равной их концентрации:
.
При расчете использованы: ионное произведение воды KW =10-14; константа диссоциации иона FeOH+ KD = 1,3.10-4, (см. Приложение 10 [3]).
Равновесные электродные потенциалы вероятных окислителей рассчитаем по уравнению Нернста:
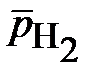= – 0,059×рН – 0,0295×lg = –0,301 + 0,0295 = –0,372 В.
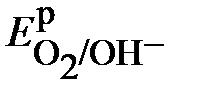= 1,227 – 0,059×рН + 0,0147×lg = 0,928 В.
Равновесный потенциал металла при 25°С рассчитываем по уравнению Нернста:
= 
+ (0,059/2)×lg 
= – 0,44 – (0,059/2)×1 = –0,47 В.
Учитывая, что
Е IЭ= – = –0,223 – (–0,47) = +0,247В > 0 – коррозия с выделением водорода (с водородной деполяризацией) возможна.
Е IIЭ= 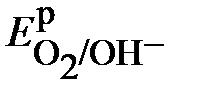– = 0,928 – (–0,47) = +1,398 >0 – коррозия с поглощением кислорода (с кислородной деполяризацией) также возможна.
Таким образом, возможна коррозия железа с протеканием на катоде двух реакций:
К: 2Н+ + 2е ® Н2
О2 + 4Н+ + 4е ®2 Н2О
А: Fe ® Fe2+ + 2e.