Занятие 1.
Построение дискретных вариационных рядов и расчет статистических характеристик
Задание 1. (с примером решения)
Проведено выборочное исследование числа клиентов, посещающих ежедневно фитнес-центр «Миринал». Для этого случайным образом на протяжении прошлого года было отобрано 40 дней. В результате отбора получена выборка 40 независимых наблюдений:
5, 7, 13, 7, 5, 9,9, 11, 15, 9, 5, 7, 5, 13, 9, 9, 15, 11, 11, 9,
13, 7, 9, 13, 11, 9, 7, 9, 7, 11, 7, 7, 13, 15, 9, 11, 13, 11, 9, 7.
Требуется представить результаты наблюдений в виде вариационного ряда. и рассчитать все его числовые характеристики – среднюю арифметическую, медиану, моду и дисперсию. Определить выборочную долю наблюдений, не превосходящих 11.
План решения задачи:
Очевидно, что исследуемая нами последовательность наблюдений представляет собой реализации дискретной случайной величины – ежедневное число клиентов фитнес-центра «Миринал». Для ее описания составим вариационный ряд. Для решения задачи целесообразно использовать программу Excel.
1. На рабочем листе расположите в виде столбца значения выборки (xi)
2. Путем использования сортировки проранжируйте данные столбца по возрастанию значений. Подсчитайте сколько разных значений принимает xi.
3. На этом же листе создайте таблицу следующего вида:
| Значения xi | ∑ | ||||||
| Частоты ni | |||||||
| Частость wi | |||||||
| Накопленная частота nx | |||||||
| Накопленная частость wx= nx/n |
Нетрудно заметить, что здесь каждое наблюдение встречается ни один раз. Так, например, 5 встречается 4 раза, 7 встречается 9 раз и т.д. Для таких одинаковых наблюдений, которые в дальнейшем будем называть вариантами, подсчитываем их количество и частость, которую определим как отношение их количества к объему выборки.
Для каждого варианта вариационного ряда найдем накопленные частоты и частости. Накопленные частоты nxi представляют собой число наблюдений не превышающих варианта xi. Их можно посчитать следующим образом. Для наименьшей (первой) варианты в вариационном ряду она будет равна соответствующей ей частоте, а для каждой последующей равна сумме частоты данного варианта и предшествующей ей накопленной частоте. Очевидно, что согласно данному определению для последней варианты вариационного ряда накопленная частота будет равна объему выборки.
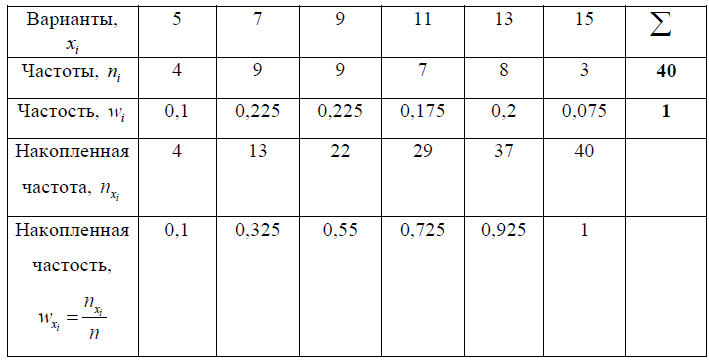
Поделив накопленные частоты на объем выборки, получим относительные накопленные частоты. Записывая полученные результаты в виде таблицы, мы тем самым получим дискретный вариационный ряд(табл. 1, первая, вторая и третья строка).
4. На основании данных таблицы использую возможности Excel постройте кумулятивную кривую и полигон частот.
Полигон частот (или относительных частот) – ломаная на плоскости, состоящая из отрезков прямых, соединяющих точки с координатами (хi, ni) или (хi, wi), i = 1, 2, …, m.
Кумулятивной кривой называется кривая накопленных частот (или накопленных частостей).
Для построения полигона частот выбираем в меню Excel: вставка - график с маркером
В контекстном меню, вызываемым правой клавишей мышки выбираем выбрать данные. Далее в таблице выделяем мышкой диапазон значений xi и частот ni
Аналогичным образом строится кумулята. Только вместо диапазона частот указывается диапазон накопленных частот.
Для полученного вариационного ряда рассчитаем статистические характеристики. Вариационный ряд имеет вид:
Дисперсией вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической, которая определяется по формулам:

Модой вариационного ряда называется варианта, которой соответствует наибольшая частота Mo.
Медианой вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений. Me
Выборочным коэффициентом асимметрии называется число определяемое по формуле, As

Выборочным эксцессом называется число E, определяемое по формуле

Выборочной долей w признака А называется отношение числа m членов выборочной совокупности с признаком А к ее объему n, т.е.

Среднюю арифметическую вариационного ряда вычислим на основании приведенной выше формулы:

Так как вариационный ряд содержит четное число членов, то медиана будет равна полусумме двух серединных наблюдений. Так как число наблюдений равно 40, то в ранжированном ряде серединными наблюдениями будут наблюдения с номерами 19 и 20. Оба эти наблюдения равны 9 и, таким образом, медиана будет равна

Так как две соседние варианты вариационного ряда (x2 =7 и x3 =9) имеют одинаковую частоту, равную 9, большую, чем для других вариант, то мода определяется неоднозначно. В этом случае говорят, что распределение имеет две моды:

Для вычисления дисперсии сначала вычислим среднюю арифметическую квадратов вариант, т.е.

Следовательно, дисперсия вариационного ряда будет равна

Выборочная доля наблюдений, не превосходящих 11, равна накопленной относительной частоте варианты равной 11 и составляет:

Примечание:
Все статистические характеристики можно вычислить с использованием встроенных функций Excel.
Задание 2.
Результаты прохождения теста оценивалось по десятибальной системе. Получены результаты 50 тестируемых:
· Составить вариационный ряд, вычислить накопленные частоты и частости. Построить полигон частот и частостей, кумулятивную кривую и эмпирическую функцию распределения.
· Рассчитать числовые характеристики – среднюю арифметическую, медиану, моду и дисперсию.
Задание 3.
На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие 60 значений:
· Построить дискретный вариационный ряд, полигон, кумуляту и эмпирическую функцию распределения.
· Рассчитать числовые характеристики – среднюю арифметическую, медиану, моду и дисперсию.
Задание 4.
Бросают 2 игральные кости. Составить распределение вероятностей случайной величины X – разность выпавших очков (Всегда положительная, либо равна нулю). Найти математическое ожидание и дисперсию. Построить закон распределения p=f(X).
| Красная кость | Зеленая кость | ||||||
| X | ||||||
| Ni | ||||||
| Pi |
n - общее число исходов (n=36)
 вероятность разности xi
вероятность разности xi
Математическое ожидание M(x)

Дисперсия

