Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.




где:
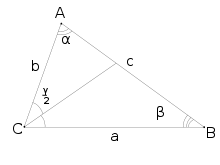
- lc — длина биссектрисы, проведённой к стороне c,
- a, b, c — стороны треугольника против вершин A, B, C соответственно,
- p — полупериметр треугольника,
- al, bl — длины отрезков, на которые биссектриса lc делит сторону c,
- α,β,γ — внутренние углы треугольника при вершинах A, B, C соответственно,
- hc — высота треугольника, опущенная на сторону c.
16. Замечательными точками треугольника являются
- Точки пересечения:
- Медиан — центроид, центр тяжести;
- Биссектрис — инцентр, центр вписанной окружности;
- Высот — ортоцентр;
- Серединных перпендикуляров — центр описанной окружности;
- Биссектрис серединого треугольника (его инцентра) — точка Шпикера;
- Точки пересечения отрезков, соединяющих вершины треугольника:
- c точками касания противоположных сторон и вписанной окружности — точка Жергона;
- c точками касания противоположных сторон и вневписанной окружности — точка Нагеля;
- c соответствующими свободными вершинами равносторонних треугольников, построенных на сторонах треугольника — точка Ферма, если в треугольнике ни один из углов не превосходит 120°, то точка Торричелли существует и совпадает с точкой Ферма;
- c соответствующими свободными вершинами треугольников, подобных исходному треугольнику и построенных на его сторонах — точки Брокара;
- Центр окружности девяти точек
17. Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СD = hc из вершины С его прямого угла.
Она разобьет данный треугольник на два прямоугольных треугольника АСD и ВСD; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС.
Все три треугольника АВС, АСD и ВСD подобны между собой.

|
Из подобия треугольников определяются соотношения:
- h=
 ac
ac  bc=ca
bc=ca  b;
b; - c = ac + bc;
- a=
 ac
ac  c
c  b=
b=  bc
bc  c;
c; - (ba)2=bcac.
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.

18.
| Построение касательной к окружности |

| Касательную из точки А к окружности можно провести следующим образом: 1. На отрезке ОА как на диаметре строят окружность радиуса R=0,5[OA]; 2. Точки 1 и 2 пересечения полученной окружности с заданной определяют положение точек касания; 3. Отрезки [ 1A ]и [ 2A ] определяют положение касательных t1 и t2 проведенных из точки А к окружности. |
 Определение 12. Касательной к окружности называется прямая, имеющая с окружностью одну общую точку.
Определение 12. Касательной к окружности называется прямая, имеющая с окружностью одну общую точку.
Теорема 7 Радиус, проведенный в точку касания окружности, перпендикулярен касательной.
Теорема 7.1 Если радиус перпендикулярен прямой в точке пересечения ею окружности, то эта прямая - касательная к этой окружности.
Для доказательства этих теорем нам нужно вспомнить, что такое перпендикуляр из точки на прямую. Это кратчайшее растояние от этой точки до этой прямой. Допустим, что ОА не перпендикулярен касательной, а есть прямая ОС перпендикулярная касательной. Длина ОС заключает в себе длину радиуса и еще некий отрезок ВС, что безусловно больше радиуса. Таким образом, можно доказывать для любой прямой. Заключаем, что радиус, радиус проведенный в точку касания, есть кратчайшее растояние до касательной из точки О, т.е. ОС перпендикулярен касательной. В доказательстве обратной теоремы будем исходить из того, что касательная имеет с окружностью только одну общую точку. Пусть данная прямая имеет еще одну общую точку В с окружностью. Треугольник АОВ прямоугольный и в нем две стороны равны как радиусы, чего быть не может. Таким образом получаем, что данная прямая не имеет больше общих точек с окружность кроме точки А, т.е. является касательной.
 Теорема 8 Отрезки касательных, проведенных из одной точки к окружности, равны, а прямая, соединяющая эту точку с центром окружности, делит угол между касательными попалам.
Теорема 8 Отрезки касательных, проведенных из одной точки к окружности, равны, а прямая, соединяющая эту точку с центром окружности, делит угол между касательными попалам.
Доказательство очень простое. Используя предыдущую теорему, утверждаем, что ОВ перпендикулярен АВ, а ОС - АС. Прямоугольные треугольники АВО и АСО равны по катету и гипотенузе (ОВ=ОС - радиусы, АО - общая). Поэтому равны и их катеты АВ=АС и углы ОАС и ОАВ.
 Теорема 9 Величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами.
Теорема 9 Величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами.
Рассмотрим угол NАВ, образованный касательной и хордой (рис11). Проведем диаметр АС. Касательная перпендикулярна диаметру, проведенному в точку касания, следовательно, ÐCAN=90о. Зная теорему 2, видим, что угол альфа (a) равен половинеполовине угловой величины дуги ВС или половине угла ВОС. ÐNAB=90о-a, отсюда получаем ÐNAB=1/2(180о-ÐBOC)=1/2ÐАОВ или = половине угловой величины дуги ВА. ч.т.д.
 Теорема 10 Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
Теорема 10 Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
На рисунке 12 эта теорема выглядит так: МА2=МВ*МС. Докажем это. По предыдущей теореме угол МАС равен половине угловой величины дуги АС, но также и угол АВС равен половине угловой величины дуги АС по теореме 2, следовательно, эти углы равны между собой. Принимая во внимание то, что у треугольников АМС и ВМА угол при вершине М общий, констатируем подобие этих треугольников по двум углам (второй признак). Из подобия имеем: МА/MB=MC/MA, откуда получаем МА2=МВ*МС
- 19. Теорема о вписанном угле:
| Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается, либо дополняет половину центрального угла до 180°. |
Пусть  — вписанный угол окружности с центром O, опирающийся на дугу AC. Докажем, что
— вписанный угол окружности с центром O, опирающийся на дугу AC. Докажем, что  . Рассмотрим три возможных случая расположения луча ВО относительно угла АВС.
. Рассмотрим три возможных случая расположения луча ВО относительно угла АВС.
1. Луч BO совпадает с одной из сторон  , например со стороной BC. В этом случае дуга AC меньше полуокружности, поэтому
, например со стороной BC. В этом случае дуга AC меньше полуокружности, поэтому 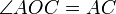 . Так как
. Так как  — внешний угол равнобедренного
— внешний угол равнобедренного  , а углы при основании равнобедренного треугольника равны, один из них это
, а углы при основании равнобедренного треугольника равны, один из них это  , значит их сумма равна
, значит их сумма равна  , a
, a  . Отсюда следует, что
. Отсюда следует, что  .
.
2. Луч BO делит  на два угла. В этом случае луч BO пересекает дугу AC в некоторой точке D. Точка D разделяет дугу AC на две дуги: AD и DC. По доказанному в п.1
на два угла. В этом случае луч BO пересекает дугу AC в некоторой точке D. Точка D разделяет дугу AC на две дуги: AD и DC. По доказанному в п.1  и
и  . Складывая эти равенства почленно, получаем:
. Складывая эти равенства почленно, получаем:  , или
, или  .
.
3. Луч BO лежит вне  . В этом случае дуга AC составляет часть дуги AD. По доказанному в п.1
. В этом случае дуга AC составляет часть дуги AD. По доказанному в п.1  и
и  .
.  . Т.к. дуга AC = AD − DC, то
. Т.к. дуга AC = AD − DC, то 
Следствия:
- · Вписанные углы, опирающиеся на одну дугу, равны.
- Угол, опирающийся на диаметр, — прямой.
- Гипотенуза прямоугольного треугольника является диаметром описанной около него окружности.
· Угол между касательной и хордой является предельным случаем вписанного угла и также равен половине дуги, на которую опирается.
Вопрос 20.
Для плоского треугольника со сторонами a, b, c и углом α, противолежащим стороне a, справедливо соотношение:
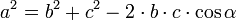 .
.
Доказательство.
Пусть есть Δ ABC.
Докажем, что

Имеем векторное равенство

Возведем в квадрат левую и правую часть равенства, получим

Или

Теорема доказана.
|
Вопрос 21.
Окружность называется вписанной в треугольник, если она касается через все его сторон.

Теорема.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.

Доказательство.
Пусть ABC данный, O – центр вписанной в него окружности, D, E и F – точки касания окружности со сторонами. Δ AEO = Δ AOD по гипотенузе и катету (EO = OD – как радиус, AO – общая). Из равенства треугольников следует, что ∠ OAD = ∠ OAE. Значит AO биссектриса угла EAD. Точно также доказывается, что точка O лежит на двух других биссектрисах треугольника. Теорема доказана.
Вопрос 22.
|
Вопрос 23.
· Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (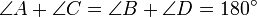 ). См. также теорема Птолемея.
). См. также теорема Птолемея.
· Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ( )
)
Вопрос 24.
Вектором называется направленный отрезок.

У вектора есть начало и есть конец. Обозначается вектор строчными латинскими буквами a, b, c,... или указанием его начала и конца, на первом месте всегда указывается начало. На чертежах вектор отмечается стрелкой. Иногда слово «вектор» не пишут, а ставят стрелочку над буквенным обозначением.
Вектор AB, AB, a

Вектор AB и вектор CD называются одинаково направленными, если полупрямые AB и CD одинаково направлены
Вектор AB и вектор CD называются противоположно направленными, если полупрямые AB и CD противоположно направлены.
a и b одинаково направленные.
a и c противоположно направленные.
Абсолютной величиной вектора называется длина отрезка, изображающего вектор. Обозначается как |a|.
Суммой векторов a(a1; a2) и b(b1; b2) называется вектор c(a1+b1; a2+b2).
Для любых векторов a(a1; a2), b(b1; b2), c(с1; с2) справедливы равенства:


Теорема
Каковы бы ни были три точки A, B и C, имеет место векторное равенство

Доказательство.
Пусть A(x1; y1), B(x2; y2), C(x3; y3) – данные три точки.
Вектор AB имеет координаты (x2 – x1; y2 – y1), вектор BC имеет координаты (x3 – x2; y3 – y2). Следовательно, вектор AB + BCимеет координаты (x3 – x1;y3 – y1). А вектор AC имеет координаты (x3 – x1;y3 – y1). Значит, AC = AB+ BC. Теорема доказана.
Произведение вектора a(a1; a2) на число λ называется вектор (λa1; λa2), т.е. (a1; a2) λ = (λa1; λa2).
Для любого вектора a и чисел λ, μ

Для любого вектора a и b и числа λ

Вопрос 25.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы либо одинаково направлены, либо противоположно направлены.
Теорема
Если есть два отличных от нуля коллинеарных вектора, то существует число λ такое, что

Доказательство.
Пусть a и b одинаково направлены.

- это векторы, которые одинаково направлены и имеют одну и ту же абсолютную величину |b|. Значит, они равны:

Когда векторы a и b противоположно направлены аналогично заключаем, что

Теорема доказана.
Теорема
Любой вектор с можно представить в виде

Вопрос 26.
|
Теорема
Равные векторы имеют равные соответствующие координаты.
Доказательство
Рассмотрим два случая: 1) векторы не лежат на одной прямой.

Пусть есть вектор a с началом в точке A (x; y) и концом в точке A` (x`; y`). При параллельном переносе получаем вектор b, у которого тогда начало будет в точке B(x+c; y+d), а конец в точке B`(x`+c; y`+d). Отсюда видно, что оба вектора будут иметь одни и тебе координаты (x-x`; y-y`).
2) векторы лежат на одной прямой.

Пусть есть прямая l на которой лежат равные векторы AA` и BB`. A(x; y), A`(x`; y`), B(x1;y1) и B(x1`; y1`). Проведем прямую l1 параллельную l и отложим на ней вектор CD равный AA` и BB`, C (x0; y0) и D (x0`; y0`). Так как AA` = CD, из предыдущего пункта x-x`=x0-x0` и y-y`=y0-y0`. С другой стороны BB` = CD и x1-x1`=x0-x0`, y1-y1`=y0-y0`. Сравнивая равенства получаем x-x`=x1-x1` и y-y`=y1-y1`. Теорема доказана.
Вопрос 27.
Теорема
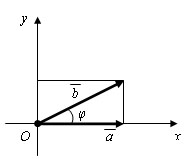
Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними.
Доказательство.
Пусть a и b – данные векторы и φ – угол между ними. Имеем:

или

Скалярное произведение ab таким образом, выражается через длины векторов a, b и a + b т. е. систему координат можно выбрать любую, а величина скалярного произведения не изменится. Выберем систему координат xy так, чтобы начало координат совпало с началом вектора a, а сам вектор лежал на положительной полуоси оси Ox. Тогда координатами вектора a будут числа |a| и 0, а координатами вектора a – |a| cos φ и |a| sin φ. По определению

Теорема доказана.
Вопрос 28.
 Доказательство. Пусть есть Δ ABC со сторонами a, b, с и углами α, β, γ. Докажем, что
Доказательство. Пусть есть Δ ABC со сторонами a, b, с и углами α, β, γ. Докажем, что  Проведем из точки С высоту CD. Тогда из Δ ACD получим:
Проведем из точки С высоту CD. Тогда из Δ ACD получим:  Если угол α тупой, то
Если угол α тупой, то  Из Δ BCD получаем
Из Δ BCD получаем  Аналогично получаем
Аналогично получаем  Теорема доказана.
Теорема доказана.
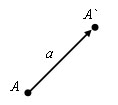 Есть вектора a. Пусть A (x; y) – начло вектора, а A` (x`; y`) – конец вектора. Координатами вектора a называются числа a1=x-x`, a2=y-y`. Для обозначения того, что вектор a имеет координаты a1 и a2, используют запись a (a1; a2) или (a1; a2). Абсолютная величина вектора a (a1; a2) равна
Есть вектора a. Пусть A (x; y) – начло вектора, а A` (x`; y`) – конец вектора. Координатами вектора a называются числа a1=x-x`, a2=y-y`. Для обозначения того, что вектор a имеет координаты a1 и a2, используют запись a (a1; a2) или (a1; a2). Абсолютная величина вектора a (a1; a2) равна  Если начало вектора совпадает с его концом, то это нулевой вектор, обозначается (0).
Если начало вектора совпадает с его концом, то это нулевой вектор, обозначается (0).