Лабораторная работа №3
Код спутников ГЛОНАСС
Цель работы: формирование и исследование псевдослучайного кода спутников ГЛОНАСС.
Порядок выполнения работы:
1. Создайте папку Cod GLONASS_My и скопируйте в нее все программы из папки CodGLONASS.
2. Запустите MatLab, откройте функцию cod_GLONASS, изучите программные процедуры и комментарии, выполните задание.
3. Задание. Откройте файл BPS_K.m. Выполните файл. Опишите полученные графики и занесите описание графиков в отчет.
Функции и файлы из папки CodGLONASS:
Функция cod_GLONASS (формирование М- последовательности спутников ГЛО-НАСС)
function [codGL, codGL_bin,Out,n]=cod_GLONASS(n);
%Имя функции: cod_GLONASS
%Функция cod_GLONASS вычисляет псевдослучайный код ГЛОНАСС
%(М-последовательность). Входные данные: n- количество символов в М-последовательности.
%Выходные данные: codGL- М- последовательность в символах "1", "-1",
%codGL_bin- М-последователности в символах "0", "1",
%Out- столбцы кодов для сравнения, n- длина кода
shift_reg=ones(1,9);%Начальное состояние регистра сдвига
for i=1:n
codGL_bin(i)=shift_reg(7); % Выход М-последователности в символах "0", "1"
modulo2 = xor(shift_reg(9),shift_reg(5));%Сложение по модулю 2 символов с 9 и 5 выходов регистра сдвига
shift_reg(2:9)=shift_reg(1:8); %Смещение данных в регистре сдвига
shift_reg(1)=modulo2; % Сложение по модулю 2 на входе 1 регистра сдвига
end
codGL=2*codGL_bin-1;%М- последовательность в символах "1", "-1"
Out=[codGL_bin' codGL' ]; % Столбцы кодов для сравнения
Файл BPS_K.m
n=511;%количество символов в М-последовательности
[codGL, codGL_bin,Out,n]=cod_GLONASS(n); %функция, формирующая М-последовательность
Dat= codGL_bin;
fDat=0.511*10^6;% скорость передачи данных
fc=4*fDat; %carrier frequency-несущая частота
fd=32*fDat; %частота дискретизации
fd_fDat=fd/fDat; %отношение частоты дискретизации к символьной скорости
t=(0:length(Dat)*fd_fDat-1)/fd; % дискретное время
t1=(0:length(codGL)*fd_fDat-1)/fd;% дискретное время
BPSK=cos(2*pi*fc*t + pi*Dat(floor(fDat*t)+1));%модулированный сигнал
%y= pmmod(Dat(floor(fDat*t)+1),fc,fd,pi);%модулированный сигнал (вариант)
y=BPSK;
%преобразование частоты
x1=y.*cos(2*pi*fc*t);
x=y.*cos(2*pi*fc*t);
[b1,a1]=butter(3,fc*2/fd);%фильтр нижних частот с максимально-плоской характеристикой
[b,a]=ellip(10,2,60,fc*2/(32*fDat));%фильтр нижних частот с эллиптической характеристикой
%фильтрация высокочастотных составляющих
x1=filtfilt(b1,a1,x1);
x=filtfilt(b,a,x);
m=3.20;
%Графика
fig1=figure;
subplot(3,1,1),plot(t,cos(2*pi*fc*t))
xlabel('а','FontSize',12,'FontName', 'TimesNewRoman')
grid on
xlim([3.07*10^(-4) m*10^(-4)])
ylim([-1.5 1.5])
%Несущая, модулированная М-последовательностью
subplot(3,1,2),plot(t,BPSK)
xlabel('б','FontSize',12,'FontName', 'TimesNewRoman')
grid on
xlim([3.07*10^(-4) m*10^(-4)])
ylim([-1.5 1.5])
subplot(3,1,3),stem(t,Dat(floor(fDat*t)+1))
xlabel('в','FontSize',12,'FontName', 'TimesNewRoman')
grid on
xlim([3.07*10^(-4) m*10^(-4)])
ylim([-1.5 1.5])
m=5;
%figure(fig1);
fig2=figure;
subplot(3,1,1), plot(t,Dat(floor(fDat*t)+1))
xlabel('а','FontSize',12,'FontName', 'TimesNewRoman')
grid on
xlim([3.07*10^(-4) m*10^(-4)])
ylim([-1.5 1.5])
subplot(3,1,2), plot(t,x1)
xlabel('б','FontSize',12,'FontName', 'TimesNewRoman')
grid on
xlim([3.07*10^(-4) m*10^(-4)])
ylim([-1.5 1.5])
subplot(3,1,3), plot(t,x)
xlabel('в','FontSize',12,'FontName', 'TimesNewRoman')
grid on
xlim([3.07*10^(-4) m*10^(-4)])
ylim([-1.5 1.5])
%Фильтры
fig3=figure;
freqz(b1,a1,512,32*fDat),
xlabel('а','FontSize',12,'FontName', 'TimesNewRoman')
fig4=figure;
freqz(b,a,512,32*fDat),
xlabel('а','FontSize',12,'FontName', 'TimesNewRoman')
Результаты выполнения файла BPS_K.m приведены на рис. 1.18 - 1.21.

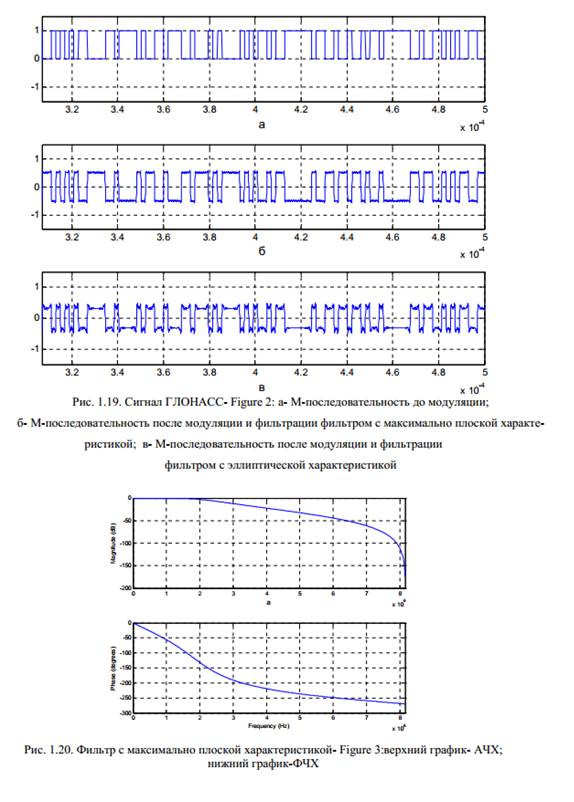
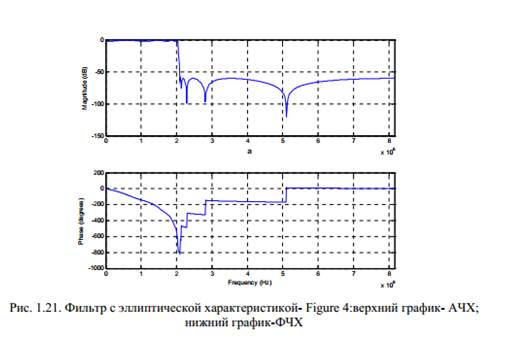
Контрольные вопросы:
1. Что такое псевдослучайный сигнал?
2. Для чего кодируются сигналы навигационных спутников?
3. Как понимать термин«отношение сигнал/шум»?
4. Опишите параметры функции корреляции.
РАЗДЕЛ 2