Инструкция по выполнению работы

Лабораторная работа № 7

Синтез оптимальных следящих систем

Цели работы

· знакомство с методами и особенностями синтеза оптимальных следящих систем при детерминированных входных сигналах

Задачи работы

· научиться строить стандартную систему в задаче синтеза оптимальных следящих линейных систем

· изучить особенности задачи синтеза

Оформление отчета

Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата Microsoft Word (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать

· название предмета, номер и название лабораторной работы

· фамилию и инициалы авторов, номер группы

· фамилию и инициалы преподавателя

· номер варианта

· краткое описание исследуемой системы

· результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.

При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.

Инструкция по выполнению работы

Основная часть команд вводится в командном окне среды Matlab. Команды, которые надо применять в других окнах, обозначены иконками соответствующих программ.

Этап выполнения задания	Команды и иллюстрации
1. Создайте новый m-файл (скрипт) с командами, которые строят модели объекта и входного сигнала: clear all; P = tf (1, [1 1]); % объект R = tf (1, [1 0]); % модель входного сигнала
2. Постройте стандартную систему и найдите оптимальный регулятор без ограничений на управление с помощью функции h2opt (файл h2opt.m нужно скопировать в рабочую папку): sys = [ R -P R 0]; C = h2opt (sys) Запустите скрипт, нажав (F5).
3. Постройте частотную характеристику полученного регулятора и сделайте выводы.	bode (C)
4. Добавьте в скрипт (в нужное место!) команды для определения установившегося значения сигнала управления и изображения по Лапласу эталонного управляющего сигнала : uInf = dcgain(tf([1 0],1)*R/P); U0 = uInf*tf(1, [1 0]);
5. Измените стандартную систему с учетом ограничения на мощность сигнала управления kU = 1; sys = [ R -P kU*U0 -kU R 0]; Снова запустите скрипт (постройте оптимальный регулятор) и постройте частотную характеристику полученного регулятора. Сравните с предыдущим вариантом.
6. Запустите Simulink, соберите модель, как показано на рисунке, и сохраните ее под именем lab7sim1.mdl. Для того, чтобы вывести на осциллограф два сигнала, используйте мультиплексор (блок Mux, группа Singal Routing).
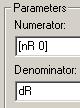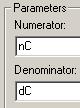7. Установите параметры блоков, как показано на рисунках: Step Signal Controller Plant Обратите внимание, что в числитель блока Signal добавлен множитель , поскольку входной сигнал – это единичная ступенька, а не дельта-функция.
8. В параметрах осциллографа снимите флажок Limit data points (ограничивать число запоминаемых точек) и установите режим сохранения данных (Save data to workspace) в виде массива (Array) с именем out.
9. Добавьте в конец скрипта команды для построения числителей и знаменателей отдельных блоков [nP,dP] = tfdata(P, 'v'); [nR,dR] = tfdata(R, 'v'); [nC,dC] = tfdata(C, 'v'); а также для запуска моделирования sim('lab7sim1'); и построения графиков figure(1); plot(out(:,1), out(:,2), out(:,1), out(:,3));
10. Запустите скрипт и перенесите полученный график в отчет.
11. Повторите расчеты при и . Сделайте выводы. Закройте файлы (скрипт и модель).
12. Теперь будем исследовать замкнутую систему управления судном по курсу. Создайте новый скрипт и добавьте в него команды для построения моделей судна, привода, измерительной системы и входного ступенчатого сигнала: clear all; P = tf (0.0694, [18.2 1 0]); % модель судна H = tf (1, [2 1]); % привод G = tf (1, [6 1]); % обратная связь R = tf (1, [1 0]); % модель сигнала
13. Добавьте команды для подготовки данных к моделированию [nP,dP] = tfdata(P, 'v'); [nR,dR] = tfdata(R, 'v'); [nH,dH] = tfdata(H, 'v'); [nG,dG] = tfdata(G, 'v');
14. Найдите передаточную функцию оптимального регулятора без учета ограничений на управление: sys = [ R -P*H R -P*H*G]; [C,Poles] = h2opt (sys)
15. Постройте частотную характеристику полученного регулятора и сделайте выводы.	bode (C)
16. Постройте оптимальный регулятор с ограничением на управление (учитывая, что установившееся значение сигнала управления для объекта с интегратором равно нулю): kU = 1; sys = [ R -P*H 0 -kU R -P*H*G]; [C,Poles] = h2opt (sys) Приведите в отчете его передаточную функцию и частотную характеристику. Сделайте выводы.
17. Запустите Simulink, соберите модель, как показано на рисунке, и сохраните ее под именем lab7sim.mdl. Для того, чтобы вывести на осциллограф два сигнала, используйте мультиплексор (блок Mux, группа Singal Routing).
18. Установите параметры блоков, как показано на рисунках: Step Signal Controller Actuator Plant Measurement Обратите внимание, что в числитель блока Signal добавлен множитель , поскольку входной сигнал – это единичная ступенька, а не дельта-функция.
19. В параметрах осциллографа снимите флажок Limit data points (ограничивать число запоминаемых точек) и установите режим сохранения данных (Save data to workspace) в виде массива (Array) с именем out. Аналогично для осциллографа Control установите вывод данных в массив u.
20. Добавьте в скрипт команды для выполнения моделирования [nC,dC] = tfdata(C, 'v'); sim('lab7sim'); построения графика (эталонный и фактический переходные процессы): figure(1); plot(out(:,1), out(:,2), out(:,1), out(:,3)); и расчета интегральных квадратических ошибок по выходу и по управлению (интегрирование методом трапеций, функция trapz): uInf = 0; % установившееся значение управления err2 = (out(:,2)-out(:,3)).^2; % квадрат ошибки errOpt = trapz(out(:,1),err2) % интегральная кв. ошибка errU2 = (u(:,2) - uInf).^2; % квадрат ошибки по управлению errU = trapz(u(:,1),errU2) % интегральная кв. ошибка
21. Установите время моделирования 100 с (меню Simulation-Simulation parameters-Stop time). Запустите скрипт и скопируйте в отчет полученный график.
22. Измените скрипт так, чтобы построить кривую качества системы (зависимость интегральный квадратических ошибок по выходу и управлению для Парето-оптимальных регуляторов): kU = [0.2 0.25 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.2 1.5 1.7 2]; uInf = 0; % установившееся значение управления errOut = []; % освободить массивы errU = []; for i=1:length(kU) fprintf('\n%g', kU(i)); % вывод текущего kU sys = [ R -P % стандартная система 0 -kU(i) R -P]; [C,Poles] = h2opt (sys); % синтез оптимального регулятора [nC,dC] = tfdata(C, 'v'); sim('lab7sim'); % моделирование err2 = (out(:,2)-out(:,3)).^2; u2 = (u(:,2) - uInf).^2; errOut(i) = trapz(out(:,1),err2); errU(i) = trapz(u(:,1),u2); end;
23. После цикла добавьте команды для построения кривой качества figure(1); plot(errOut, errU, '-o'); xlabel('Error'); ylabel('Control error');
24. Запустите скрипт на выполнение. Скопируйте в отчет полученную кривую качества. Сделайте выводы.