Лабораторная работа №8-9
«Реализация методов математической обработки информации
средствами электронных таблиц»
Задание 1.
1. Ознакомьтесь с материалом кейса «Вероятностные модели». Определите основные черты метода Монте-Карло.
2. Проанализируйте эффективность данного способа для решения простейшей вероятностной задачи: «Определить вероятность выпадения орла (выпадения решки) при однократном бросании монеты».
3. В электронных таблицах постройте экспериментальную вычислительную модель решения данной задачи.
Решение:
1. Метод Монте-Карло базируется на использовании больших серий испытаний со случайными параметрами, причем точность полученных результатов зависит от количества проведенных опытов. Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину Х, математическое ожидание которой равно а: М(Х)=а.
Практически же поступают так: производят n испытаний, в результате которых получают n возможных значений Х; вычисляют их среднее арифметическое 
и принимают x в качестве оценки (приближённого значения) a* искомого числа a:
.
Поскольку метод Монте-Карло требует проведения большого числа испытаний, его часто называют методом статистических испытаний. Теория этого метода указывает, как наиболее целесообразно выбрать случайную величину Х, как найти её возможные значения. В частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*.
2. Требуется проанализировать эффективность метода Монте-Карло для решения простейшей вероятностной задачи: «Определить вероятность выпадения орла (выпадения решки) при однократном бросании монеты».
Рассмотрим случайную величину X, равную 0 при выпадении решки, и равную 1 при выпадении орла. Вероятности обоих значений будем считать одинаковыми. Тогда математическое ожидание M(X)=0.5*0+0.5*1=0.5, дисперсия D(X)=M(X2)-M(X) 2 =0.5*02+0.5*12 - 0.52 = 0.25 = 1/4, среднее квадратическое ожидание равно s=1/2 = 0.5. В этом случае с надёжностью g верхняя граница ошибки 
. Для вероятности p=0.95 t=1.96, поэтому 
. Это означает, что необходимо повторить порядка 10000 опытов, чтобы ошибка не превышала 1%.
3. Создадим файл рабочей книги Excel с именем lab8-9.xls, в котором на листе “Лист1” разместим расчетные формулы.
В ячейки A2:J11 поместим формулы вида =ЕСЛИ(СЛЧИС()>=0,5;1;0),
В ячейку C12 – формулу =СУММ(A2:J11), в ячейку C14 – формулу =C12/C13, в ячейку C15 – формулу =0,98/КОРЕНЬ(C13).
Расчетная таблица имеет вид:
В результате находим, что искомая вероятность равна 0.5 с точностью до 0.098. Следует отметить, что значения вероятности изменяются при каждом пересчете таблицы, и могут значительно отличаться от 0.5.
Задание 2.
1. Решите задачу[1] по образцу.
Экскурсионная поездка
В конце учебного года администрация школы организовала для всех желающих экскурсию и, получив информацию из классов о числе экскурсантов, заказала соответствующее количество автобусов. Зная, что в каждый автобус входит ровно 45 пассажиров, завуч по внеклассной работе уже начала было заполнять таблицу 2, но с ней заспорила классный руководитель 10 В класса. Конечно, всем ребятам из одного класса хотелось бы ехать в одном автобусе. Завуч сказала, что все равно так не получится и кому-то придется ехать в разных автобусах...
Таблица
| Класс | Едут на экскурсию | Первый автобус | Второй автобус | Третий автобус |
| 10 А | ||||
| 10 Б | ||||
| 10 В | ||||
| 10 Г | ||||
| 11 А | ||||
| 11 Б | ||||
| 11 В | ||||
| 11 Г |
Давайте попробуем с помощью электронной таблицы подобрать такой вариант, чтобы было как можно меньше недовольных. Эта задача отнюдь не простая. Как вы думаете, что должно стоять в ячейках таблицы на пересечении номеров автобусов и классов? Количество человек (как это сделано в таблице 1)? Но если класс целиком садится в один автобус, оно и так нам известно.
Итак, что общего имеют между собой первый автобус и, скажем, 10 А класс? Ну конечно же 10 А класс либо едет в этом автобусе, либо нет. Стало быть, и в соответствующей ячейке должны стоять либо единица, либо нуль. А для контроля заполняемости автобуса необходимо добавить еще одну строку (табл.):
Таблица 1
| Класс | Едут на экскурсию | Первый автобус | Второй автобус | Третий автобус |
| 10 А | ||||
| 10 Б | ||||
| 10 В | ||||
| 10 Г | ||||
| 11 А | ||||
| 11 Б | ||||
| 11 В | ||||
| 11 Г | ||||
| Итого в автобусе |
Можете считать, что перед вами электронная таблица, предназначенная для решения задачи об организации экскурсии. Естественно, что пересчет количества людей в автобусе производится автоматически, т.е. у этих ячеек заполнен «подвальный» этаж. А как он заполнен, вы, наверно, уже сами догадались. Выполняя лабораторную работу, вы закончите работу по рассаживанию школьников в автобусы.
Рассаживаем учащихся по автобусам
1. Заполните таблицу.
Таблица 2
| А | В | С | D | E | |
| Класс | Едут на экскурсию | Первый автобус | Второй автобус | Третий автобус | |
| 10 А | |||||
| 10 Б | |||||
| 10 В | |||||
| 10 Г | |||||
| 11 А | |||||
| 11 Б | |||||
| 11 В | |||||
| 11 Г | |||||
| Итого в автобусе |
2. В ячейках столбцов С, D и Е должны находиться либо 1 (единица), либо 0 (нуль), либо ничего (что аналогично нулю). Единица ставится в ячейку тогда и только тогда, когда класс, указанный в строке, целиком едет в автобусе, указанном в столбце. Обратите внимание, что при занесении чисел они прижимаются к правому краю столбца.
3. Перед тем как начинать «рассаживание» классов по автобусам, необходимо заполнить формулами нижний этаж ячеек С10, D10, Е10. Так, в ячейке С10 должна стоять формула
С2*В2 + СЗ*ВЗ + С4*В4 + С5*В5 + С6*В6 + С7*В7 + С8*В8 + С9*В9.
Это позволит в дальнейшем контролировать загрузку автобусов. Запишите нужные формулы в соответствующие ячейки. Обратите внимание, что в качестве знака умножения в формулах, записываемых в ячейки электронной таблицы, употребляется «*».
4. Ваша задача – расставить единицы и нули в таблице таким образом, чтобы в каждом автобусе ехало не более 45 человек. Выполните эту работу.
Составители учебника предлагают решить нам эти задачи методом подбора, используя электронную таблицу. Для реализации оптимизационных расчетов в Open Calc необходимо использовать надстройку Поиск решения с помощью команды системного меню Сервис. Модель использует целевую функцию, которая записывается в виде формулы в отдельной ячейке. Для целевой функции указывается: максимизация, минимизация или равенство фиксированному значению. В процесс поиска решения изменяются значения в указанных ячейках, соответствующие переменным, при соблюдении ограничений.
Построим математическую модель задачи. Введем переменную хij, значение которой равно 1, если i -й класс едет в j -ом автобусе, и равно 0 в противном случае. Тогда условие того, что 10 А класс может ехать только в одном автобусе выражается равенством х 11 + х 12 + х 13 = 1. Аналогично записываются равенства относительно других классов. Таким образом, получаем систему: 
. Обозначим число учащихся, едущих в первом автобусе через у 1, тогда у 1 = 23 х 11 + 17 х 21 + 22 х 31 + 8 х 41 + 18 х 51 + 6 х 61 +19 х 71 + 14 х81. Аналогично у 2 = 23 х 12 + 17 х 22 + 22 х 32 + 8 х 42 + 18 х 52 + 6 х 62 +19 х 72 + 14 х82 – число учащихся, едущих во втором автобусе, у 3 = 23 х 13 + 17 х 23 + 22 х 33 + 8 х 43 + 18 х 53 + 6 х 63 +19 х 73 + 14 х83 – число учащихся, едущих в третьем автобусе. Так как в каждый автобус можно посадить не более 45 человек, то у 1 ≤ 45, у 2 ≤ 45 и у 3 ≤ 45. Обозначим число всех учащихся, поместившихся в автобусы через F, тогда F = у 1 + у 2 + у 3.
Таким образом, задача состоит в определении таких значений неизвестных хij (
), удовлетворяющих системе уравнений , ограничениям у 1 ≤ 45, у 2 ≤ 45 и у 3 ≤ 45, при которых достигается максимальное значение функции F = у 1 + у 2 + у 3.
Подготовим данные оптимизационной модели на рабочем листе. Заполните таблицу.
Таблица 3
| А | В | С | D | E | F | |
| Класс | Едут на экскурсию | Первый автобус | Второй автобус | Третий автобус | Ограничения | |
| 10 А | ||||||
| 10 Б | ||||||
| 10 В | ||||||
| 10 Г | ||||||
| 11 А | ||||||
| 11 Б | ||||||
| 11 В | ||||||
| 11 Г | ||||||
| Итого в автобусе |
Двойной рамкой в таблице выделен блок ячеек С2:E9, в котором содержатся значения переменных.
1. В ячейку F2 введите формулу = SUM(C2:E2), которая соответствует левой части равенства х 11 + х 12 + х 13 =1.
2. Скопируйте эту формулу в ячейки F3:F9.
3. В ячейку С10 введите формулу =SUMPRODUCT($B$2:$B$9;C2:C9), которая соответствует у 1.
4. Скопируйте эту формулу в ячейки D10 и E10.
5. В ячейку F10 введите формулу =SUM(C10:E10), которая соответствует целевой функции F = у 1 + у 2 + у 3.
6. В диалоговом окне Поиск решения укажите:
– Установить целевую ячейку: $F$10
– Равной: максимальному значению
– Изменяя ячейки: $C$2:$E$9
7. Для ввода ограничений, нажмите кнопку Добавить
8. В диалоговом окне Добавление ограничения для ввода первого ограничения $F$2:$F$9 = 1укажите:
– Ссылка на ячейку: $F$2:$F$9
– Раскройте кнопку списка и выберите знак =
– Ограничение: 1
9. Аналогично введите ограничения $C$2:$E$9 = двоичное и $C$10:$E$10 ≤ 45 и нажмите кнопку Ок.
10. В диалоговом окне Поиск решения нажмите кнопку Параметры, установите Линейная модель и нажмите Ок.
11. В диалоговом окне Поиск решения нажмите кнопку Выполнить. На экране диалоговое окно Результаты поиска решения в котором сообщается о результате решения. Укажите: Сохранить найденное решение и нажмите Ок, чтобы вернуться к рабочему листу. В блоке ячеек $C$2:$E$9, где хранились переменные, появится решение задачи. Приведем один из возможных вариантов ответов (табл.).
Таблица 4
| Класс | Едут на экскурсию | Первый автобус | Второй автобус | Третий автобус | Ограничения |
| 10 А | |||||
| 10 Б | |||||
| 10 В | |||||
| 10 Г | |||||
| 11 А | |||||
| 11 Б | |||||
| 11 В | |||||
| 11 Г | |||||
| Итого в автобусе |
Из таблицы видно, что в первом автобусе едут 10 Б, 10 Г и 11 А классы. Во втором – 10 В и 11 В, в третьем – 10 А, 11 Б и 11 Г. Из 127 желающих попасть на экскурсию всех можно разместить в три автобуса, в первом поедут 43 человека, во втором 41 и в третьем – 43.
Решение:
В файле рабочей книги Excel с именем lab8-9.xls на листе “Лист2” разместим указанные в задании расчетные формулы. Запустим “Поиск решения” с параметрами, указанными на рисунке.
В итоге получим следующее решение:
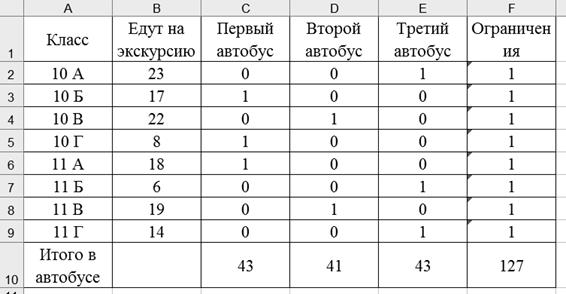
Из таблицы видно, что в первом автобусе едут 10 Б, 10 Г и 11 А классы. Во втором – 10 В и 11 В, в третьем – 10 А, 11 Б и 11 Г. Из 127 желающих попасть на экскурсию всех можно разместить в три автобуса, в первом поедут 43 человека, во втором 41 и в третьем – 43.
Задание 3.
Используя предыдущее решение, выполните решение данной задачи. При создании математической модели проанализируйте, как будут отличаться данные расчета и ограничения от шаблона, заявленного в предыдущем решении.
Перевозка грузов
Перед диспетчером компании «ПАНУРАЛТРАНССИБСЕРВИС» встала непростая задача. Три грузовика компании должны забрать с разных предприятий Новосибирска груз (табл.) и доставить его в Омск. Грузоподъемность каждой машины – 12 т, и хотелось бы распределить весь груз примерно поровну. Ну, быть может, допустив 100-150 кг перегрузки у какого-нибудь грузовика.
Таблица
| Наименование оборудования | Количество | Вес одной упаковки (кг) | Первый грузовик | Второй грузовик | Третий грузовик |
| Станки (штуки) | |||||
| Трубы (упаковки) | |||||
| Буровое оборудование (ящики) | |||||
| Отдел очный камень (ящики) | |||||
| Промышленные электромоторы (штуки) | |||||
| Кабель (бухты) | |||||
| Всего груза в машине (кг) |
Видимо, вы уже поняли, что и в этом случае диспетчеру поможет электронная таблица.
Как и в первой задаче, постараемся понять связь между строками и столбцами. Она похожа на то, что было в предыдущем задании, но есть и отличие. А именно вовсе необязательно грузить, например, весь кабель на одну машину. Поэтому в ячейках могут стоять не одни только нули и единицы. В данном случае связь заключается в том, сколько упаковок (штук, ящиков) груза берет конкретная автомашина.
Используя свои навыки работы с электронными таблицами, выполните задания:
1. Заполните таблицу:
Таблица
| А | В | С | D | E | F | |
| Наименование оборудования | Количество | Вес одной упаковки (кг) | Первый грузовик | Второй грузовик | Третий грузовик | |
| Станки (штуки) | ||||||
| Трубы (упаковки) | ||||||
| Буровое оборудование (ящики) | ||||||
| Отделочный камень (ящики) | ||||||
| Промышленные электромоторы (штуки) | ||||||
| Кабель (бухты) | ||||||
| Итого вес груза |
2. В столбцах D, Е и F должны находиться числа, определяющие, сколько упаковок или штук данного груза берет соответствующий грузовик.
3. Перед тем как начинать распределение груза, необходимо заполнить формулами нижний этаж ячеек D8, Е8, F8. Так, в ячейке D8 должна стоять формула C2*D2+C3*D3+C4*D4+C5*D5+C6*D6+C7*D7.
Это позволит в дальнейшем контролировать загрузку грузовиков. Запишите нужные формулы в соответствующие ячейки.
4. Кроме того, необходимо заполнить формулами «подвальный этаж» ячеек с F2 по F7, предоставляя компьютеру автоматически загружать третий грузовик теми товарами, которые не взяли первые два. Так, в ячейке F2 должна стоять формула В2 – D2 – Е2. Воспользуйтесь возможностью копирования формулы, чтобы заполнить оставшиеся ячейки с F3 по F7.
5. Ваша задача – манипулируя с числами в столбцах D и Е, так распределить товары, чтобы загрузка каждой из автомашин не превышала 12 т более чем на 100-150 кг.
Решение:
В файле рабочей книги Excel с именем lab8-9-2.xls на листе “Лист3” разместим указанные в задании расчетные формулы. В диалоге “Поиск решения” введем ограничения так, как показано на рисунке:
В ограничениях требуется, чтобы значения в изменяемых ячейках D2:E7 были целыми и не отрицательными. Загрузка каждого автомобиля не должна превышать 12150 кг – это 3-е ограничение. Так как целевая функция не определена, то потребуем, чтобы в ячейке D2 был нуль. Если бы приемлемое решение не было бы найдено, то можно было бы поменять ячейку D2 на любую другую. Запустим “Поиск решения” с параметрами, указанными на рисунке, и находим следующее решение:
В таблице видим, что загрузка 1 и 2 грузовика не превышает 12150 кг, загрузка 3-го меньше 12000 кг. Все грузы полностью распределены между грузовиками.
[1] Информатика: Учеб. пособие для 10-11 кл. общеобразоват. учреждений / А.Г. Гейн, А.И. Сенокосов, Н.А. Юнерман. – 2-изд. – М.: Просвещение, 2001. – 255с.