Имеется отрезок произвольной длины. Необходимо разделить его пополам, пользуясь только циркулем и не прибегая к помощи линейки.
По сути, всё, что можно сделать сначала – это прочертить
Из концов отрезка две окружности радиусом равным длине отрезка.
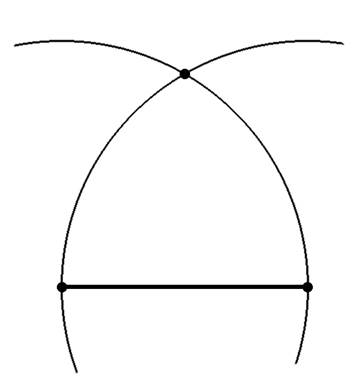
Концы отрезка и точка пересечения окружностей образуют
равносторонний треугольник.
Пользуясь этим методом можно построить сетку из вспомогательных точек сколь угодно большого размера. Нам потребуется всего два ряда точек лежащие на прямой, являющейся продолжением отрезка и параллельной ей прямой проходящей через вершину построенного нами первого треугольника.

В равностороннем треугольнике любая высота (перпендикуляр, проведенный из вершины к противоположной стороне) является одновременно медианой (линией соединяющей вершину и середину противоположной стороны) а значит, чтобы получить
середину отрезка, достаточно провести через вершину треугольника окружность, центр которой лежит на прямой, равноудаленной от прямой, являющейся продолжением исходного отрезка и параллельной ей прямой проходящей через вершину треугольника. Центром окружности может служить середина отрезка, концы которого расположены на вышеупомянутых прямых
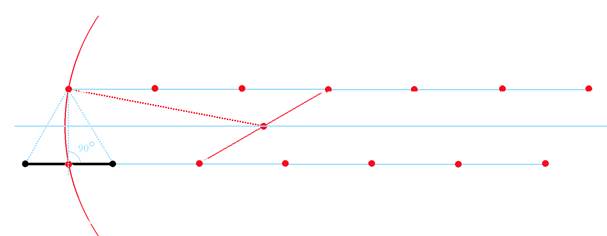
Но, по условию задачи, пользоваться линейкой мы не можем
(все линии на рисунках начерчены лишь для пояснения), а значит
в окончательном построении нам придется пользоваться лишь точками из верхнего и нижнего рядов или точкой из верхнего ряда и точкой лежащей на исходном отрезке. Концы вспомогательного отрезка соединить линией мы тоже не сможем, поэтому его центр нам придется получать тоже с помощью единственно циркуля.
Тут нам на помощь придет теорема Пифагора, а точнее её частный случай со сторонами треугольника 3,4 и 5.Угол между сторонами
3 и 4 – прямой, и, следовательно, если мы возьмем отрезок, равный
5 и из одного конца прочертим окружность радиусом 3, а из другого радиусом 4, получим прямоугольный треугольник.
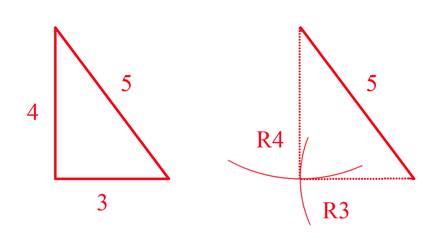
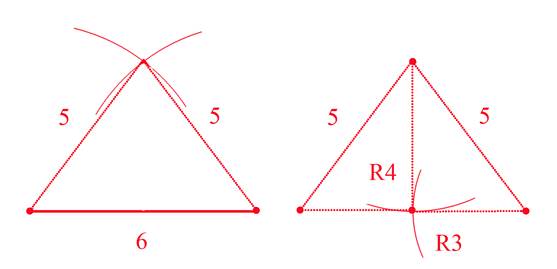
И как следствие мы можем, зная это, получить середину отрезка длиной 6, пользуясь только циркулем.
Применив эти построения к нашему случаю, получим такую методу:
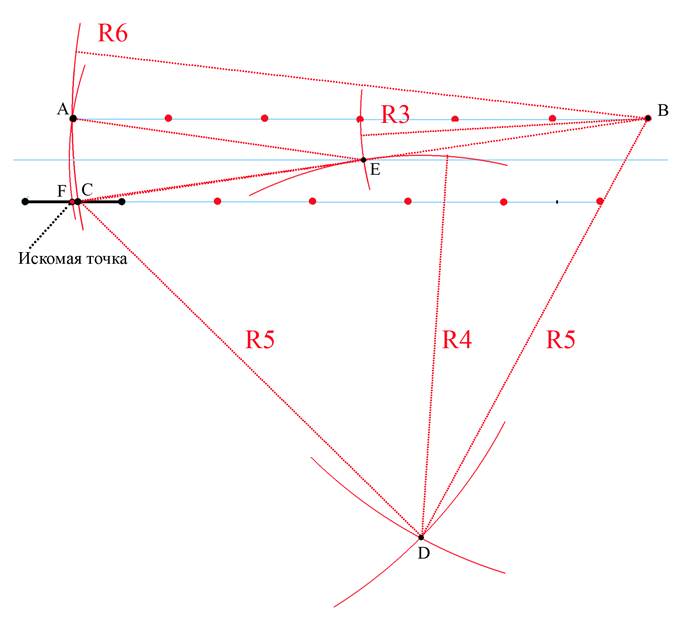
1.Проведя из концов исходного отрезка дуги окружностей радиусом
равным длине отрезка получим на их пересечении точку A – вершину равностороннего треугольника.
2.Сходным образом построим два ряда точек, обозначенных на
рисунке красным. Расстояние между двумя соседними точками равно длине исходного отрезка – условной единице. Точки верхнего ряда лежат на одной прямой и нижнего ряда – аналогично.
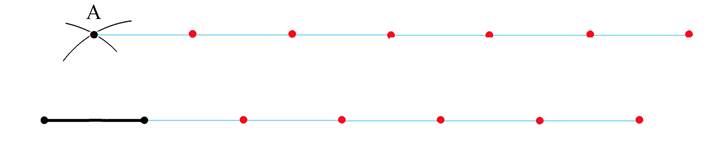
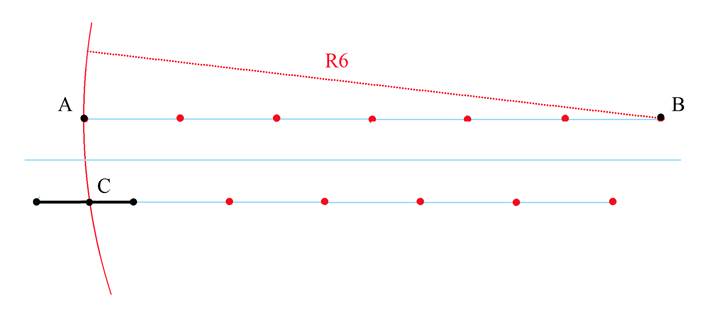
3.Отсчитав от точки А шестую точку, обозначим ее B.
Из точки B проведем дугу окружности радиусом BA = 6
На пересечении этой дуги с исходным отрезком отметим точку C.
BC = BA = 6
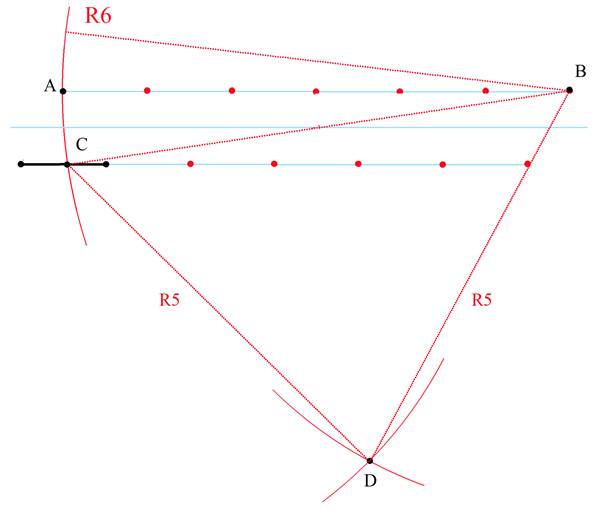
4.Отложим от точки В пять точек и этим радиусом проведем дугу окружности. Этим же радиусом проведем дугу из точки С.
Точку пересечения этих дуг обозначим D.
DC = DB, треугольник CDB – равнобедренный
5. Из точки В проведем дугу радиусом 3 а из точки D радиусом 4.
На пересечении дуг получим точку Е – середину отрезка ВС.
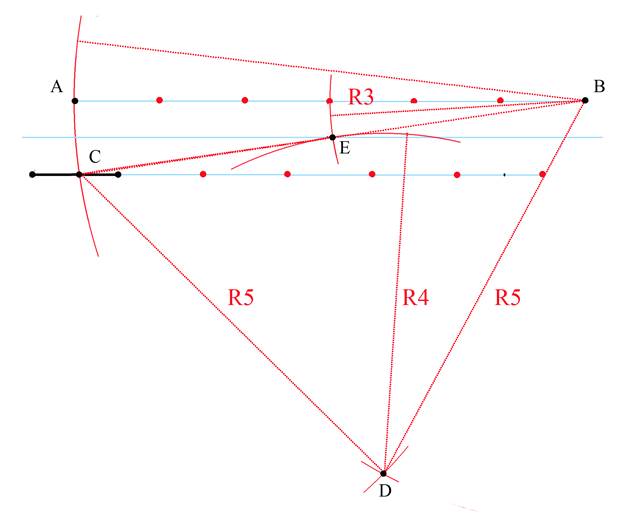
Как мы ранее обосновали, точка Е, являясь серединой отрезка ВС,
(как следствие теоремы Пифагора), лежит на прямой, равноудаленной от прямой, являющейся продолжением исходного отрезка и параллельной ей прямой, проходящей через точку А,
а значит равноудалена от точки А и искомой точки, являющейся серединой исходного отрезка. Следовательно, приняв ее за центр
и проведя окружность через точку А, на пересечении этой окружности с исходным отрезком получим искомую точку.
6. Что мы и сделаем.
Точка F и есть искомая точка – середина исходного отрезка
Таким образом, задача деления отрезка пополам решается при помощи одного лишь циркуля.
Это станет видно, когда мы уберем из рисунка вспомогательные лини, с помощью которых иллюстрировалось объяснение и
покажем окружности, использовавшиеся для построения промежуточных точек, ранее не показанные, чтобы не отвлекать от объяснения.

Вот собственно и всё.