Расчет внецентренно-сжатой колонны

Исходные данные:

Тяжелый бетон класса 20, подвергнутого тепловой обработке при атмосферном давлении берем: = 15 МПа, = 1,4 МПа, = 11,5 МПа, = 0,9 МПа, = 24000 МПа.

Продольная рабочая арматура класса A-III Ø 10-40 мм.

Поперечная арматура Вр-I.

Граничное значение относительной высоты сжатой зоны бетона .

Сечение колонны b*h = 400*400 м.

Высота этажа H = 2,9 м.

Вес колонны одного этажа: = 0,4*0,4*2,9*25*1,1*0,95 = 11,704 кН.

Продольная сила от перекрытия 8 вышележащих этажей:

= 8*35,3*2,8*0,95 = 751,18кН.

Вес от 8 вышележащих колонн: = 3*22,572 = 67,716 кН.

Итого: = 1472,36+67,716 = 1540,08 кН, в том числе длительно действующая сила = 3*24,53*5,4+3*22,572 = 465 кН.

Усилия из расчета рамы:

M = -44,3кН*м; Q = 25,7кН (см. приложение «SCAD»).

Изгибающий момент от длительно действующей нагрузки: = 29,46кН*м.

3.3.1 Расчет по прочности сечений, нормальных к продольной оси колонны

Вычисляем эксцентриситеты по формулам:

;

.

По [24, п.1.21] принимаем во внимание случайный эксцентриситет , обусловленный не учтенными в расчете факторами:

1) ;

2) ,

где – расчетная длина внецентренно–сжатого элемента, определяется по формуле: = H = 2,8 м. Расчеты выполняем с учетом наибольших по абсолютной величине эксцентриситетов в направлении двух осей сечений (в плоскости изгиба и в перпендикулярной плоскости).

По [24] предварительно задаемся коэффициентом армирования m= = 0,005÷0,035, задаемся m = 0,005.

Как правило, наименьший расход арматуры получается при несимметричном армировании.

Определив расчетную длину = Н =2,8 м по [24, п.3.25], вычислим отношение , следовательно, необходимо учитывать влияние прогиба на несущую способность колонны.

Вычисляем относительный эксцентриситет:

, который должен быть не менее

> .

Вычисляем коэффициент, учитывающий влияние на прогиб элемента из тяжелого бетона длительности действия нагрузки по [24, формула (21)]:

.

Определяем следующие величины:

– момент инерции сечения ;

– момент инерции площади сечения арматуры при = 360-30 = 330 мм,

.

Коэффициент приведения: = 8,33.

Вычисляем условную критическую силу N_cr:

.

Определяем значение коэффициента h, учитывающего влияние прогиба, на значение эксцентриситета продольного усилия по [24, формула (19)]:

.

Вычисляем плечо приложения продольной силы относительно оси растянутой арматуры:

.

Проверяем условие:

.

.

Если , то прочность сжатых элементов рассчитывают по формуле: .

Площадь поперечного сечения продольной рабочей арматуры:

Принимаем конструктивно 2Æ10 A – III c = 157 мм².

Проверяем условие: по [24, табл.38] при 17£ l_o/i £35 минимальная площадь сечения продольной арматуры min m*b*h_o = 0,0001*400*360 =144 мм² < = 402 мм².

Радиус инерции сечения колонны в плоскости изгиба:

i = = 0,4/3,464 = 0,1155 м.

Отношение l_o/i = 2,8/0,1155 = 24,24.

Принимаем 2Æ16 A – III c = 402 мм²

Так как < 0, то сжатая арматура по расчету не требуется, но устанавливается конструктивно.

Проверяем коэффициент армирования:

m = .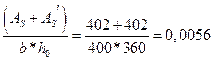

От принятого ранее он отличается на 0,0056/0,005=1,12<5%

Решение можно считать найденным.

3.3.2 Расчёт железобетонной консоли колонны

Исходные данные:

Расчетная сила, передаваемая ригелем на консоль из расчета рамы Q = 112,99 кН.

Класс бетона – тяжелый бетон В20, подвергнутый тепловой обработке при атмосферном давлении.

Сопряжение ригеля с колонной обетонированное; зазор между торцом ригеля и гранью колонны а₃ =20 мм. Обетонирование сопряжения производится до приложения нагрузки на смонтированный ригель.

Назначаем продольную и поперечную арматуру консоли из стали класса A – III. Закладные детали – из прокатной уголковой стали.

Ширину консоли принимаем равной ширине колонны b = 400 мм.

Определяем минимально допустимый вылет консоли из условия обеспечения ее прочности на смятие в месте опирания ригеля по формуле:

Т.к. принимается конструкция ригеля и колонны по серии 1.020-1, вылет консоли принимаем 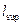=140мм. Ширина наклонной сжатой полосы , где l _sup-длина площадки передачи нагрузки вдоль вылета консоли, т.е. равная вылету консоли при опирании на нее ригеля; l _b =140*0,5 =70 мм, где θ =30^о, где sin θ =0,5 для sin 30^о.

Расчет консоли на действие поперечной силы для обеспечения прочности по наклонной сжатой полосе производим по формуле:

.

Вычисляем коэффициент j_w2 по формуле:

j_w2 = 1 + 5*a*m_WI;

= 8,33.

Требуемая площадь продольной арматуры: .

Требуемая полезная высота консоли:

.

Принимаем h_o = 180 мм; h = 180+30 = 210мм.

Изгибающий момент в сечении примыкания консоли к колонне:

Требуемое сечение арматуры класса А–III, которая огибает консоль, т. е. при :

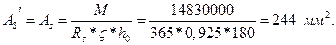
Можно принять 2Æ14 класса A – III c = 308 мм².

Вычисляем коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента, и коэффициент армирования:

;

j_w2 = 1+5*8,33*0,00385= 1,16.

Проверяем условие:

Q £ 0,8*j_w2*g_b2*R_b*b* l _b*sinq = 0,8*1,16*0,9*11,5*400*140*0,5 = 268930 Н > Q = 112990 Н.

Условие выполняется, но правая часть условия принимается не более:

Q = 3,5*R_bt*b*h_o = 3,5*0,9*400*180 = 226800 H и не менее определяемой по формуле:

где j_b2 = 2 – коэффициент, учитывающий влияние вида бетона (тяжелый бетон В20);

j_f = 0 – коэффициент, учитывающий влияние сжатых полок;

j_n = 0 – коэффициент, учитывающий влияние продольных сил.

Со £ 2*hо = 2*180 =360 м,

,

т.е. условие удовлетворяется.

Проверяем условие: , где j_b1 определяем по формуле: .

Q £ 0,3*1,16*0,885*0,9*11,5*400*180 = 229507 Н.

Q_b = 58320 < 229507 Н.

Условие удовлетворяется, следовательно, прочность консоли по наклонной сжатой полосе обеспечена.

Расчет ригеля

3.4.1 Расчет по прочности сечений, нормальных к продольной оси ригеля

Исходные данные:

Бетон тяжелый класса В20; R_b,ser = 15,0 МПа; R_bt,ser = 1,4 МПа; R_b = 11,5 МПа; R_bt = 0,9 МПа; E_b = 27´10³ МПа – для бетона естественного твердения; E_b = 24*10³ МПа – для бетона подвергнутого тепловой обработке при атмосферном давлении, g_b2 = 0,9.

Арматура:продольная рабочая из стали класса A – III; R_s,ser = 390 МПа; R_s = 365 МПа – расчетное сопротивление арматуры диаметром 10-40 мм; E_s = 200000 МПа.

В крайнем пролете ригеля максимальные изгибающие моменты: по оси колонны М=-174,1 кН*м, Q=133,66кН, в середине пролета от опоры М=84,4 кН*м, Q=10,33кН (см. приложение «SCAD»).

Ригель таврового сечения с полкой внизу, рассчитываем как прямоугольное сечение шириной b=300мм, высотой h=450мм.

Колонны сечением b_к*h_к = 0,4*0,4 м.

Характеристика сжатой зоны бетона по формуле при g_b2 = 0,9:

w = α – 0,008*g_b2*R_b = 0,85-0,008*0,9*11,5 = 0,767

Граничное значение относительной высоты сжатой зоны бетона по формуле:

,

где - напряжение в арматуре (в МПа), принимаем для арматуры классов A-I, A-II, A-III:

= 365 МПа;

- предельное напряжение в арматуре сжатой зоны, принимаем при равным 400 МПа, а для конструкций из тяжелого, мелкозернистого и легкого бетонов, если учитывается коэффициент , равным 500 МПа.

Соответственно величина a_R = 0,432.

Сечение ригеля по грани колонны.

Изгибающий момент:

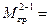
= 147,38 кH*м.

Коэффициент a₀ находим по формуле:

= 0,297 < = 0,432

Соответственно z = 0,823.

Требуемое сечение растянутой арматуры по формуле:

= 1226,55 мм²

По сортаменту арматурной стали можно принять 2Æ25 A-III+2Æ16 A-III c A_S = 1290 мм².

Сечение ригеля в пролете.

M₁ = 84,4 кH*м.

= 0,17 < = 0,432

Соответственно z = 0,906.

Требуемое сечение растянутой арматуры:

= 638 мм².

Принимаем 4Æ16 A – III c A_S = 804 мм².

3.4.2 Расчет по прочности сечений, наклонных к продольной оси ригеля

Данные для подбора сечений: g_b2 = 0,9; поперечная арматура класса А-III Æ 10 – 40 мм; R_s,ser = 390 МПа; R_s = 365 МПа; R_sw = 290 МПа.

Расчет на действие поперечной силы.

Проверяем условие: Q < 0,3*j_w1*j_b1*g_b2*R_b*b*h_o,

где j_w1 – коэффициент, учитывающий влияние хомутов, нормальных к продольной оси элемента определяется по формуле j_w1 = 1 + 5*a*m_W,

a = E_S/E_b = 200000/27000 = 7,4, предварительно возьмем m = 0,001,

j_w1 = 1 + 5*7,4*0,001 =1,037.

Коэффициент j_b1 определяется по формуле j_b1 = 1 – b*R_b,

где b = 0,01 – коэффициент для тяжелого бетона: j_b1 = 1 – 0,01*11,5 = 0,885.

0,3*1,037*0,885*0,90*11,5*300*400 = 341952 H > Q = 133660 H,

При этом для хомутов, устанавливаемых по расчету, должно удовлетворяться условие (83) по [24]:

при b=300 мм.

Находим величину Q_b по формуле:

Q_b = 0,6*g_b2*R_b*b*h_o = 0,6*0,9*0,9*300*400=58320 H < Q=133660 H, следовательно, необходимо рассчитать поперечную арматуру.

По [24, пп. 3.32, 5.22, 5.26] требуется определить шаг поперечных стержней в приопорной зоне ригеля: S₁ £ h/3 = 450/3 = 150 мм < 300 мм.

Принимаем S₁ = 150 мм.

Усилие в хомутах на единицу длины элемента:

, отсюда:

Принимаем 2Æ6 A – III с A_SW = 57 мм².

Определим соответственно:

Определяем несущую способность наклонного сечения по формуле при j_b2 = 2:

Q_b + Q_SW = 2

= 183536,5 H > Q = 133660 H,

Следовательно, прочность наклонного сечения обеспечена.

В средней части ригеля шаг поперечных стержней:

S₂ = 3*h/4 = 3*450/4 = 337,5 мм.

Принимаем S₂ = 350 мм и сечение стержней Æ6 A – III без расчета.

3.4.3 Расчёт на действие изгибающего момента

Прочность наклонных сечений на действие изгибающего момента обеспечивается анкеровкой растянутой продольной арматуры.

При определении площади поперечного сечения растянутой арматуры M_max необходимо уменьшить количество этой арматуры в приопорных участках, т.к. в них изгибающие моменты значительно меньше M_max.

Обрыв стержней в пролете не снижает несущую способность в ригеле, а дает большой экономический эффект, потому что, уменьшается расход стали.

Рисунок 3.4 – Ригель многоэтажной рамы с эпюрами изгибающих моментов и поперечных сил от распределенной нагрузки

Определим предельный изгибающий момент, растягивающий опорную арматуру без учета обрываемого стержня, поскольку А_s = 1290 мм² < т. е. х < 0:

.

По эпюре моментов определим расстояние х от опоры до места теоретического обрыва первого стержня из уравнения:

откуда

Поперечная сила в месте теоретического обрыва равна:

Определим величину q_sw:

Вычислим длину w, на которую надо завести обрываемый стержень за точку тео­ретического обрыва:

Следовательно, расстояние от опоры до места обрыва стержня может быть принято равным x + w = 39+126 = 165мм.

Определим необходимое расстояние 1_an от места обрыва стержня до вертикального сечения, в кото­ром он используется полностью:

= 725 мм > 165 мм.

Следовательно, оборвем стержень на расстоянии 725мм от опоры.

В соответствии с [24, п.5.20] продольное армирование изгибаемых элементов (ригелей) шириной более 150 мм производится рабочими стержнями, число которых должно быть не менее двух (доводим до опоры).

На основании [24, п.5.22] поперечная арматура должна охватывать крайние продольные рабочие стержни. Расстояние между поперечными стержнями у каждой поверхности элемента должно быть не более 500 мм и не более удвоенной ширины грани элемента.

При насыщении сборного элемента продольной арматуры (более 3%) хомуты устанавливаются на расстоянии не более 10d и не более 300 мм.

Соотношение диаметров поперечных и продольных стержней в сварных каркасах устанавливается из условия сварки по соответствующим нормативным документам.

В соответствии с [24, п.5.27] расстояние между поперечными стержнями принимается:

– на приопорных участках (равных при равномерно распределенной нагрузке 1/4 пролета) при высоте сечения h £ 450 мм – не более h/2 и не более 150 мм; при высоте сечения h > 450 мм – не более h/3 и не более 300 мм;

– на остальной части пролета при высоте сечения h > 300 мм – не более 3/4h и не более 500 мм.

Защитный слой бетона в ригелях принимается, как правило, не менее диаметра стержня, а при высоте элемента 250 мм и более – 20 мм в соответствии с [24, пп.5.4 и 5.5].

3.4.4 Расчет наклонных сечений в подрезках

Исходные данные: хомуты и отогнутые стержни из ар­матуры класса А-III, диаметром соответственно 6 и 10 мм (A_sw = 57мм²; A_s,inc = 314мм²); площадь сечения дополнительных хомутов у под­резки A_{sw 1} = 157мм² (2 Æ 10); продольная арма­тура класса А-III; поперечная сила на опоре Q = 133,66кН.

 

 

Рисунок 3.5 – Узел примыкания ригеля к консоли колонны с помощью подрезки

Проверим прочность наклонного сече­ния подрезки по поперечной силе согласно [24, п. 3.31], принимая h ₀ = 220 мм, b = 300 мм, j_{b 2} = 2:

При значении с, равном расстоянию от опоры до первого груза - с = 1,5 м, имеем (j_{b 3} = 0,6):

.

следовательно, принимаем Q_b = 35,64*10³ H;

Принимаем При этом c ₀ < c = 1,5 м и c ₀ > h ₀.

Тогда Q_b + q_swc ₀ +R_swA_{sw 1} = 35,64*10³ + 108,3*400 + 290*157 = 124,5*10³ H > Q = 133,66 кН, т.е. даже без учета отгибов прочность подрезки по по­перечной силе обеспечена.

Проверим достаточность дополнительных хому­тов и отгибов. Из рисунка 3.5. q = 45°; h ₀ = 450-50 = 400мм; h ₀₁ = 220мм; R_swA_{sw 1} + R_swA_s,inc sin45° = 290 *157+ 290 *314*0,707 = 109,9*10³ H > Q = = 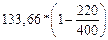60,15кН.

Проверим прочность наклонного сечения, про­ходящего через входящий угол подрезки, на дей­ствие изгибающего момента.

Невыгоднейшее значение с определим, учитывая в числителе отгибы и дополни­тельные хомуты и принимая F_i = 0 и q = 0:

Поскольку продольная арматура короткой кон­соли заанкерена на опоре, учитываем эту арматуру с полным расчетным сопротивлением, т. е. с R_s = 365 МПа.

Из рисунка 3.5. А_s = А_s^/= 308мм² (2 Æ 14). По­скольку A_s = А_s^/, x = 0, тогда z_s = h ₀₁ – а’ = 220 – 50 = 170мм.

Принимая a ₁ = 30 мм, получим

Проверим условие, принимая:

т. е. прочность наклонного сечения обеспечена.

Определим необходимую длину заведения про­дольной растянутой арматуры за конец подрезки:

Выясним необходимость постановки анкеров для нижней арматуры балки. Для этого проверим наклонное сечение, расположенное вне подрезки и начинающееся на расстоянии h ₀ – h ₀₁ = 400-220 = 180мм от торца балки. Тогда l_x = 180-10= =170мм.

Длину анкеровки для нижней арматуры опре­делим по [24, поз. 1 табл. 45], из которой при классе бетона В20 и классе арматуры А-III находим l _an = 29, отсюда l_an = 29 *16 = 464 мм > l_x = 170мм.

Расчетное сопротивление нижней арматуры снизим умножением на коэффициент т. e. R_s = 365*0,366 = 133,6МПа.

По рисунку 3.5. А_s = 804 мм² (4 Æ 16).

Учитывая, что в пределах длины l_x =170м два верхних стержня имеют по одному приваренному вертикальному стержню, а два нижних стержня имеют по одному вертикальному и один горизонталь­ный приваренный стержень, увеличим усилие R_sA_s на величину N_w. Принимаем n_w = 5, d_w = 6мм, j_w = 200:

Отсюда

Принимая b= = 300 мм, определим высоту сжатой зоны х:

и, следовательно, z_s = h ₀ -a’ = 400-50 = 350 мм.

Невыгоднейшее значение с равно:

т. е. при таком значении с наклонное сечение не пере­секает продольную арматуру короткой консоли. Принимаем конец наклонного сечения в конце ука­занной арматуры, т. е. на расстоянии w ₀ = 670 мм от подрезки, при этом с = 1234,2 мм. Расчетный мо­мент М в сечении, проходящем через конец наклон­ного сечения, равен:

;

,

где a ₁ = 150мм.

Проверим условие:

т.е. прочность наклонного сечения обеспечена, и, следовательно, анкера для нижней арматуры не тре­буются.

Расчет коротких консолей на действие поперечной силы для обеспечения прочности по наклонной сжатой полосе между грузом и опорой должен производиться из условия: .

Проверим условие, принимая l_sup = 140 мм, a_x = 80 мм, h ₀₁ – a’ = 220 – 50 = 170 мм (см. рисунок 3.5.). Тогда

Принимая m_w = 0 и заменяя 0,8 на 1,0, имеем R_bbl_sup sin² q = 11,5*300*140*0,374 = 180,6*10³H < 3,5 R_btbh ₀₁ = 3,5*0,9*300*220 = 207,9*10³ H, т. е. правую часть условия оставляем равной 207,9 кН.

Поскольку Q = 133,66кН < 207,9кН, прочность сжа­той полосы обеспечена.

При жестком соединении ригеля и колонны с замоноличиванием стыка и привариванием нижней арматуры ригеля к арматуре консоли через закладные детали продольная арматура проверяется из условия:

Принимаем l ₁ = l_sup + a_x = 220 мм, h ₀ = 270 мм, A_s = 308 мм² (2Æ 14):

т. е. продольной арматуры в короткой консоли поставлено достаточно.