2.1. Изотермы Ван-дер-Ваальса
Главное достоинство уравнения Ван-дер-Ваальса состоит в том, что оно описывает картину превращения газа в жидкость, т.е. изменение агрегатного состояния вещества. А наиболее содержательные результаты получаются путем анализа изотерм Ван-дер-Ваальса.
Преобразуем уравнение Ван-дер-Ваальса, приведя к уравнению третьей степени по объему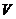 
.
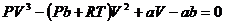(2.1)
Это уравнение изотермы, в которое давление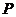 
входит в качестве параметра, имеет, вообще говоря, три корня. Поскольку коэффициенты уравнения (2.1) вещественны, то либо все три корня вещественны, либо
вещественный только один.
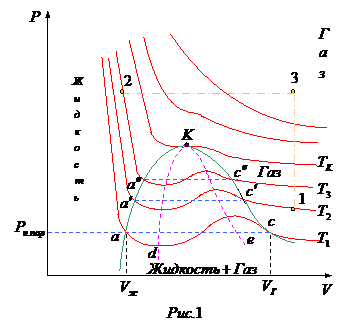
На рисунке 
представлены изотермы,
рассчитанные по уравнению Ван-дер-Ваальса.
Каждому корню на плоскости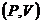 
соответствует точка, в которой изобара
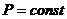пересекает изотерму.
При достаточно высоких температурах
изотерма Ван-дер-Ваальса имеет вид
монотонно опускающейся кривой, близкой
к изотермам идеального газа.
В этом случае будет одна точка
пересечения изобары с изотермой и,
соответственно, и уравнение (2.1) имеет
единственный корень.
При более низких температурах и
соответствующих давлениях уравнение (2.1)
имеет три различных корня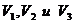 
.
В этой области температур изотерма содержит
волнообразный участок, на котором она
сначала плавно спускается вниз, затем
монотонно поднимается вверх и снова
монотонно опускается.
Область немонотонной зависимости сужается с ростом температуры и при некоторой температуре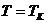 
исчезает.
При этой промежуточной температуре все три корня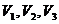 
становятся равными друг другу. Такая
температура и соответствующая ей изотерма называются критическими.
Соответствующие критической температуре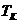 
значения объема 
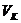и давления 
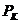также называются
критическими. Говорят, что вещество находится в критическом состоянии, если значения его объема, давления и температуры равны критическим.
В критической точке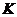 
параметры 
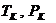и 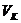имеют значения, характерные для данного вещества.
Критические параметры.
Критические параметры можно определить, заметив, что критическая точка является точкой перегиба изотермы, касательная в которой горизонтальна. Поэтому в точке 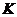должны соблюдаться соотношения
, 
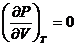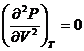. (2.2)
Решая эти уравнения совместно с уравнением состояния
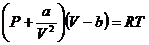, (2.3)
мы получим значения критических параметров.
Однако к тому же результату можно прийти иначе, что мы и сделаем. Для нахождения критических параметров перепишем уравнение (2.1) в виде
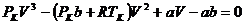. (2.4)
Поскольку в критической точке все три корня уравнения совпадают и равны 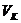, уравнение (2.1) должно приводиться к виду:
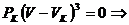
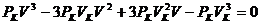. (2.5)
Сравнивая коэффициенты в (2.4) и (2.5) при соответствующих степенях 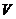, получаем три уравнения:
, 
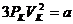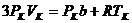, (2.6)
откуда находим
, 
, 
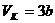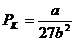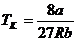. (2.7)
В качестве единиц измерения объема, давления и температуры можно принять их критические значения. Макроскопические параметры газа, записанные в таких единицах, называются приведенными:
, 
, 
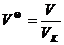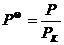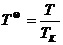. (2.8)
Уравнение состояния, записанное в безразмерных постоянных (2.7) называется приведенным уравнением состояния. Для газов Ван-дер-Ваальса
, 
, 
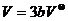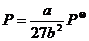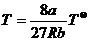. (2.9)
Приведенное уравнение состояния принимает вид:
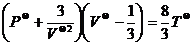. (2.10)
Приведенные уравнения состояния одинаковы для всех веществ.
В таком виде уравнение состояния не содержит никаких индивидуальных констант и поэтому обладает большей общностью, чем уравнение Ван-дер-Ваальса, из которого оно получено.
Не следует думать, что критическое состояние и критические параметры вещества являются связанными исключительно с уравнением Ван-дер-Ваальса. Исторически к понятию критического состояния вещества пришли путем анализа экспериментально полученных изотерм, не используя какие бы то ни было уравнения состояния вещества. В то же время представляет несомненный интерес установить связь между критическими явлениями, уравнением состояния и общими условиями термодинамического равновесия. Сравнительно просто это можно сделать, если для проведения рассуждений использовать уравнение Ван-дер-Ваальса, рассматривая его не как истинное, а как “модельное” уравнение состояния системы.
Для того чтобы состояния, определяемые уравнением Ван-дер-Ваальса, могли быть реализованы, они, эти состояния, должны быть термодинамически
устойчивы.
Одним из необходимых условий
термодинамической устойчивости физически
однородного вещества является выполнение
неравенства
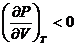. (2.11)
Это условие имеет простой физический смысл:
при изотермическом увеличении давления объем
тела должен уменьшаться. Для анализа изотерм
Ван-дер-Ваальса это означает, что при возрастании
объема 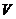все изотермы должны монотонно
опускаться.
Однако ниже критической температуры
изотермы Ван-дер-Ваальса содержат участки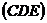 
,
вдоль которых давление растет по мере увеличения
объема, т.е.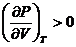 
.
Точки, лежащие на таких участках, соответствуют неустойчивым состояниям вещества, которые практически реализованы быть не могут.
Следовательно, реальная (наблюдаемая в опыте) изотерма распадается на две ветви, отделенные друг от друга, причем левой и правой ветвям изотермы соответствуют различные агрегатные состояния вещества.
Естественно предположить, что правая ветвь, характеризуемая относительно большими значениями объема или малыми значениями плотности (понятно, что масса вещества постоянна), должна описывать газообразное состояние вещества.
Напротив, левую ветвь, характеризуемую относительно малыми объемами и, следовательно, большими плотностями, следует отнести к жидкому состоянию вещества.
На промежутке между рассматриваемыми ветвями изотермы происходит процесс перехода газа в жидкость и обратно.
Т.о., мы распространяем уравнение Ван-дер-Ваальса и на область жидкого состояния. Таким путем удается получить удовлетворительное качественное описание явления перехода вещества из одного агрегатного состояния в другое.
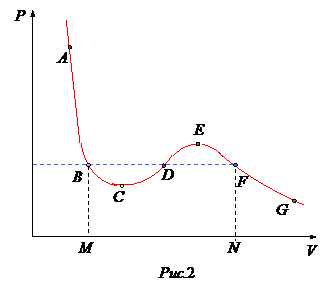
Обратимся к опыту. Возьмем достаточно разреженный газ при температуре ниже критической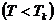 
, исходное состояние которого изображается на диаграмме 
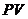(рис.2) точкой 
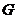. Поддерживая температуру 
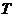постоянной, начнем квазистатически сжимать газ. Точка, изображающая состояние газа будет перемещаться по изотерме вверх. При этом оказывается, что, начиная с точки 
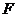, лежащей на изотерме, давление в рассматриваемой системе перестает повышаться, и система распадается на две физически однородные части, или фазы: газообразную и жидкую.
Процесс изотермического сжатия такой двухфазной системы изображается горизонтальным участком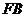 
. Плотности жидкости и газа во время сжатия остаются неизменными и равными их значениям в точках 
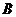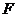и , соответственно. Количество вещества в газообразной фазе по мере сжатия непрерывно уменьшается, а жидкой фазе – увеличивается. По достижении точки 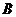все вещество перейдет в жидкое состояние.
Такой ход изотерм был впервые обнаружен на опыте голландским ученым ван Марумом (1750-1837) при исследовании аммиака.
В дальнейшем были предприняты многочисленные попытки перевода газов в жидкое состояние путем сжатия, в частности Фарадеем (1791-1867). Он применил комбинированный метод, который, по существу используется в современных установках для ожижения газов. В этом методе Фарадей сочетал сжатие газа с его охлаждением.
Однако долгое время оставалось неясным, почему при сжатии одних газов происходит сжижение, а других – нет. Ответ на этот вопрос получил английский физик Томас Эндрюс (1813-1885). В работах, ставших классическими, он исследовал изотермы углекислоты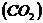 
и ввел понятие критической температуры. Оказалось, что только ниже этой температуры на изотермах появляются горизонтальные участки, на которых изотермическое сжатие газа приводит к конденсации, а не к увеличению давления.
Т.о., было установлено следующее.
Сжатием газ можно превратить в жидкость только тогда, когда его температура ниже критической. Это невозможно сделать никаким повышением давления, если температура газа выше критической.
Сказанное означает, что при высоких температурах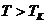 
вещество может находиться только в одном (газообразном) состоянии. При температурах 
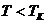вещество может находиться в трех состояниях: двух стабильных – жидком 
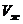и газообразном 
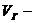и одном нестабильном.
Если рассматривать фазовый переход жидкость – газ, выбрав в качестве исходного состояния жидкое (точка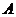 
), то при изотермическом расширении точка, изображающая состояние вещества, будет перемещаться вниз по изотерме, пока не достигнет положения 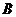, начиная с которого появляется новая фаза – газообразная. Процесс расширения двухфазной системы пойдет вдоль горизонтального участка 
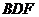изотермы, и в точке 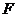все вещество перейдет в газообразное состояние. Дальнейший изотермический процесс расширения однофазной системы (газа) идет по участку 
.
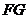При специальных условиях можно реализовать состояния, изображаемые участками изотермы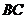 
и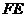 
.
Это, так называемые, метастабильные состояния. Участок изотермы 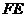относится к пересыщенному (переохлажденному) пару, а участок 
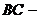к перегретой жидкости. Каждая из этих фаз может существовать до тех пор, пока она не граничит с другой, более устойчивой фазой. Так, если ввести в пересыщенный пар каплю жидкости, то он переходит в насыщенный. Перегретая жидкость закипает, если в нее попадают пузырьки газа (пара).
Вещество из состояния 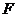в состояние 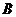можно перевести двумя изотермическими процессами:
1. по изотерме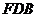 
двухфазного состояния вещества и
2. по теоретической изотерме физически однородного вещества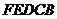 
.
Положение горизонтального участка изотермы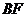 
можно определить, пользуясь термодинамическим равенством Клаузиуса
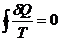, (2.12)
которое мы применим к квазистатическому круговому процессу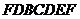 
. Поскольку указанный процесс является изотермическим (
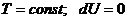), равенство Клаузиуса принимает вид
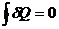, или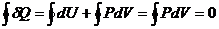 
, (2.13)
откуда следует
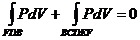, (2.14)
т.е.
. (2.15)
Т.о., площадь прямоугольника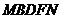 
должна быть равна площади криволинейной фигуры 
.
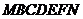Это значит, что прямую 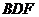(рис.2) надо провести так, чтобы были одинаковыми площад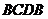и 
и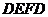 
.
Полученный результат называется правилом Максвелла.
Возьмем в двухфазной области какую-либо точку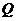 
. Вещество, состояние которого изображается
этой точкой, состоит из жидкости и газа. Найдем относительное содержание этих фаз. Удельные объемы (обратные плотности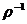 
) жидкости и газа изобразятся отрезкам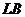и 
и 
, а удельный объем всего вещества – отрезком 
.
Пусть в точке масса газа равна 
,
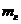а масса жидкости –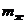 
, тогда
.
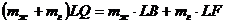Отсюда
,
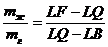или
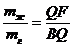, (2.16)
т.е. точка 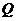делит отрезок 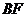на части,
обратно пропорциональные массам жидкости
и газа.
Полученный результат называется правилом рычага.
Т.о., экспериментально полученная изотерма позволяет установить, какие доли от полного количества вещества находятся в жидком и газообразном состояниях в каждой точке двухфазной области.
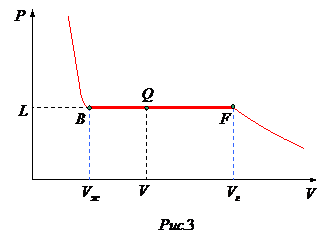
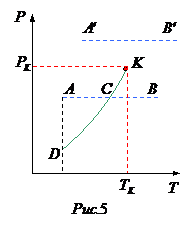
Вернемся к анализу изотерм, изображенных на рис.1.
Точки прямой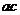 
отвечают равновесию жидкости и её насыщенного пара. При более низких давлениях (за областью, где возможно одновременное существование газа и жидкости) изотерма характеризует свойства газа. Левая, почти вертикальная ветвь изотермы отражает малую сжимаемость жидкости. Участок 
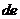физически неосуществим, т.к. здесь происходит увеличение объема 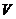при увеличении давления 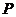. Совокупность точек 
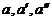и 
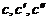определяет кривую, называемую бинодалью, которая очерчивает область совместного существования газа и жидкости. В однофазной области, лежащей в координатах 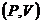выше бинодали, состояние вещества абсолютно устойчиво в том смысле, что любой возникший в жидкости пузырек пара со временем схлопнется, а любая капелька, попавшая в пар, полностью испарится. Линия 
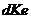- спинодаль, или «кривая потери термодинамической устойчивости» – очерчивает область неустойчивых состояний. Участк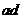и 
и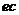 
на нижней изотерме и аналогичные участки других изотерм – область между бинодалью и спинодалью – относятся соответственно к перегретой жидкости и переохлажденному пару (метастабильные состояния).
Мы рассмотрели переход вещества из газообразного состояния в жидкое (рис. 2,3), имея возможность наблюдать, где начинается и как происходит это превращение. Однако тот же переход можно произвести иначе.
Нагреем газ (см. рис. 1) при постоянном объеме так, чтобы его температура и давление стали выше критических (вертикальная прямая 13). Затем, поддерживая давление постоянным, охладим газ ниже критической температуры (горизонтальная прямая 32). В итоге мы придем в состояние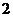 
, т.е. сконденсируем газ в жидкость.
Принципиальное отличие этого способа изменения агрегатного состояния вещества от рассмотренного выше, заключается в том, что в этом случае свойства вещества будут меняться непрерывно, никаких скачкообразных превращений вещества из газа в жидкость наблюдаться не будет (или наоборот, из жидкости в газ), и вещество все время будет оставаться физически однородным (не имеет смысла говорить, что в какой-то момент произошла конденсация).
Т.о., вещество из одного состояния в другое можно перевести, непрерывно меняя его свойства.
Когда состояние вещества изображается точкой, лежащей выше бинодали, то различие между газом и жидкостью будет только количественным, но не качественным. Именно это имея в виду, говорят, следуя Ван-дер-Ваальсу, о непрерывности жидкого и газообразного состояний вещества.
Только в области, лежащей под бинодалью, где вещество распадается на две фазы, отделенные друг от друга границей раздела и обладающие различными физическими свойствами, оправдано различать жидкое и газообразное состояния вещества.
Условие равновесия фаз.
Определим ещё раз понятие «фаза вещества».
В термодинамике фазой называют термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний (других фаз) того же вещества.
Заметим, что иногда и неравновесное метастабильное состояние вещества называют фазой (метастабильной).
Другое определение. Фазой называется макроскопическая физически однородная часть вещества, отделенная от остальных частей системы границами раздела, так что она может быть извлечена из системы механическим путем.
Важнейшим вопросом при рассмотрении системы, состоящей из нескольких фаз, является выяснение условий её равновесия. Условия равновесия такой системы включают в себя механическое и тепловое равновесия.
Необходимым условием механического равновесия является равенство давлений по разные стороны границы раздела соприкасающихся фаз.
Для теплового равновесия необходимо, чтобы все фазы системы имели одну и ту же температуру.
Для однофазного вещества выполнение этих условий обеспечивает равновесие системы.
Однако для неоднофазной системы равенство давлений и температур ещё не означает, что система находится в равновесии, так как соприкасающиеся фазы могут превращаться друг в друга. Такие превращения называются фазовыми превращениями. Состояние же равновесия системы характеризуется тем, что масса каждой фазы системы остается неизменной. В то же время при фазовых превращениях одни фазы растут, другие уменьшаются и даже могут совсем исчезнуть. Например, сообщение системе некоторого количества тепла приведет к изменению массы жидкости и газа, поскольку часть жидкости перейдет в пар. Именно такие процессы отображают горизонтальные участки изотерм Ван-дер-Ваальса (, ).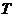
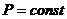Таким образом, должно быть выполнено ещё одно – третье – необходимое условие равновесия – равновесие по отношению к взаимным превращениям фаз.
Здесь мы ограничимся рассмотрением фазовых превращений только химически однородных веществ.
Условие равновесия фаз можно получить из теорем термодинамики. Поскольку при равновесии системы должны оставаться постоянными её температура 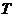и давление 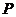, то при протекании в такой системе самопроизвольных процессов её термодинамический потенциал
(*)
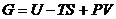должен убывать и достигать минимума в состоянии устойчивого равновесия.
Рассмотрим систему, состоящую из двух фаз, способных превращаться одна в другую. Пусть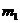 
и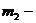 
массы первой и второй фаз соответственно, а полная масса системы
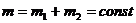. (2.17)
Как все термодинамические функции термодинамический потенциал есть аддитивная величина, поэтому для всей системы он равен сумме термодинамических потенциалов образующих систему фаз:
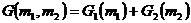. (2.18)
Поскольку массы фаз связаны соотношением (2.17), термодинамический потенциал системы можно рассматривать как функцию только одной из переменных, например, :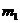
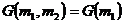. (2.19)
Введем в рассмотрение удельный термодинамический потенциал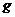 
, т.е. потенциал, отнесенный к единичной массе фазы, тогда
, 
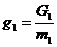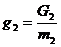(2.20)
и термодинамический потенциал всей системы
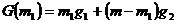. (2.21)
Поскольку при фазовом превращении (горизонтальный участок изотермы Ван-дер-Ваальса) температура 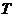и давление 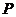системы и образующих её фаз постоянны, то требование минимума термодинамического потенциала означает здесь требование минимума функции 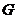относительно переменной 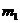, т.е. должно выполняться
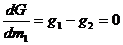. (2.22)
Отсюда получаем
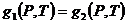. (2.23)
Полученное соотношение (2.23) выражает условие равновесия фаз двухфазной системы – равенство удельных термодинамических потенциалов образующих систему фаз.
С микроскопической точки зрения равновесие фаз не является статическим, так как происходит непрерывное превращение одной фазы в другую, но обязательно выполняется условие
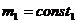и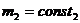 
,
т.е. в равновесии масса каждой фазы неизменна.
Изобразим состояния вещества точками на плоскости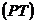 
. Каждая точка на этой плоскости соответствует однородному (однофазному) состоянию вещества. Исключение составляют точки линии 
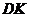, определяемой уравнением (2.23). На линии 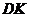удельные термодинамические потенциалы обеих фаз одинаковы, и обе фазы находятся в равновесии друг с другом.
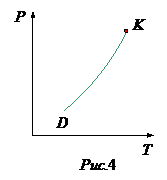Для определенности рассмотрим процессы испарения и конденсации.
Тогда каждая точка линии 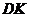изображает либо жидкость, либо её пар,
либо смесь этих фаз в любых пропорциях, в зависимости от её положения
на этой линии.
Условие равновесия фаз 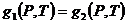можно рассматривать как
уравнение, связывающее в процессе фазового превращения давление 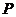и
температуру 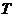в системе, т.е. фазовый переход происходит при строго
определенной зависимости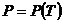 
.
Если решить уравнение (2.23) относительно 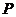, то уравнение кривой
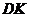представится в виде
.
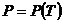Это уравнение дает зависимость давления насыщенного пара от температуры.
Кривая 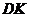называется кривой равновесия жидкости и её насыщенного пара, или кривой испарения.
Рассмотрим процесс фазового превращения с помощью приведенной диаграммы.
Пересечем кривую испарения горизонтальной прямой – изобарой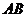 
при давлении ниже критического. В точке 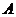вещество находится в жидком состоянии, поскольку давление в этой точке выше давления
насыщенного пара (точка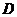 
) при той же температуре. Под таким давлением пар существовать не может и скоденсируется в жидкость.
Нагрев жидкости при постоянном давлении соответствует движению на диаграмме изображающей
точки вправо от точки 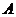к точке 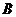. В точке 
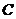пересечения изобары
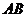с кривой испарения 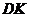начнется испарение жидкости. В течение
всего времени испарения температура жидкости и её насыщенного пара
будет оставаться неизменной. Когда вся жидкость испарится,
изображающая точка при дальнейшем подводе тепла будет перемещаться
вправо по изобаре. Участок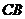 
соответствует нагреванию пара при
постоянном давлении. Т.о., точки плоскости, лежащие левее кривой
испарения 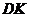, изображают жидкое состояние вещества, а точки,
лежащие правее этой кривой, – газообразное.
Рассмотрим теперь изобару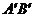 
, проходящую выше критической
точки. В этом случае при изобарическом нагревании или охлаждении
никаких превращений жидкости в пар или обратно не произойдет.
Т.о., кривая 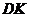должна иметь конечную длину и заканчиваться
сверху в критической точке.
Перейти из произвольной начальной точки 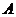в произвольную конечную точку 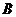можно так, чтобы пересечь кривую испарения 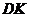. Тогда наблюдается фазовое превращение. Если же совершить переход между этими состояниями, обойдя критическую точку 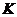без пересечения кривой испарения, то фазовый переход не произойдет. Вещество все время будет оставаться физически однородным, а его свойства будут меняться непрерывно.
Соотношение (2.23)
,
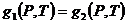выражающее условие равновесия двух фаз, описывает кривые различных фазовых превращений, например,
испарение – конденсация;
плавление – отвердевание (кристаллизация);
сублимация – кристаллизация.
Все эти фазовые превращения сопровождаются выделением или поглощением теплоты (скрытая теплота) и относятся к фазовым переходам первого рода.
Уравнение Клапейрона-Клаузиуса.
Пусть по-прежнему уравнение (2.23) выражает условие равновесия жидкой и газообразной фаз. Найдем наклон кривой испарения, т.е. вычислим производную давления насыщенного пара по температуре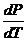 
.
При смещении вдоль кривой испарения удельные термодинамические потенциалы обеих фаз, удовлетворяя уравнению (2.23), должны иметь одинаковые приращения:
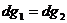. (2.24)
Из термодинамики (*) следует, что приращение удельного термодинамического потенциала можно записать в виде:
,
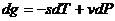где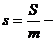 
удельная энтропия и 
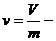удельный объем соответствующей фазы.
Тогда уравнение (2.24) принимает вид:
,
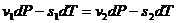или
, (2.25)
где индекс 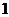относится к пару, а индекс 
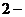к жидкости.
Фазовые превращения, вообще говоря, сопровождаются скачкообразными изменениями энтропии. Это значит, что при таких превращениях поглощается или выделяется теплота. Так при переходе единичной массы вещества из газообразного состояния 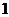в жидкое состояние 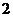выделяется теплота (при обратном переходе такая же теплота будет поглощаться):
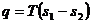. (2.26)
Отметим, что переход совершается квазистатически при постоянной температуре, и, следовательно, при постоянном давлении, поскольку речь идет о насыщенном паре.
Здесь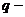 
удельная теплота испарения. В общем случае теплота 
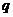называется удельной теплотой фазового превращения.
Если теперь теплоту 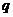ввести в уравнение (2.25), то получим важное соотношение, называемое уравнением Клапейрона – Клаузиуса:
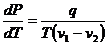. (2.27)
С молекулярной точки зрения легко понять, почему при испарении жидкости затрачивается теплота. Скорости молекул жидкости подчиняются распределению Максвелла. Вылететь в окружающее жидкость пространство могут только наиболее быстрые молекулы, способные преодолеть силы притяжения, действующие в поверхностном слое жидкости. В результате ухода наиболее быстрых молекул жидкость охлаждается, а для поддержания её температуры постоянной требуется подвод теплоты.
Уравнение Клапейрона-Клаузиуса можно получить, проведя цикл Карно с двухфазной системой, состоящей из жидкости и её насыщенного пара.
Поскольку давление насыщенного пара однозначно
определяется его температурой, то для такой системы
изотерма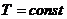 
одновременно будет являться и
изобарой 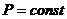. На диаграммах 
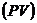изотермы
двухфазных систем изображаются горизонтальными
прямыми.
Обозначим на рис.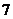 
начальное состояние двухфазной
системы точкой 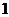. Будем квазистатически подводить теплоту
к рассматриваемой системе, приведя её в тепловой контакт с
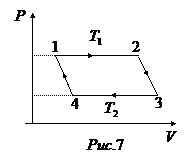нагревателем. Жидкость при этом начнет испаряться, а
система совершать работу,
поднимая, например,
нагруженный поршень.
Испарив единицу массы жидкости (точка ), выведем систему из
теплового контакта и адиабатически изолируем. После этого заставим
систему адиабатически расширяться по бесконечно короткой адиабате 
до достижения температуры холодильника 
. В качестве холодильника
мы будем использовать тепловой резервуар, температура которого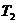
бесконечно мало отличается от температуры нагревателя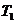 
. Далее по
изотерме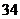 
и адиабате 
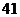вернем систему в исходное состояние. В результате система совершит бесконечно малый цикл Карно.
Получив от нагревателя количество теплоты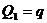 
, система совершила на изотерме 
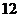работу
,
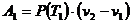увеличив свой объем на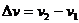 
, и работу
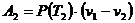
на изотерме 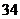. Если пренебречь работой совершенной системой на адиабатических участках, как величиной
более высокого порядка малости, то полная работа системы будет равна
.
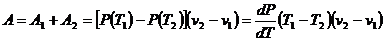По теореме Карно имеем
.
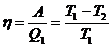Подставляя сюда значения 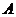и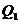 
и заменяя 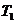на 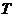, снова приходим к уравнению Клапейрона-Клаузиуса.
Уравнение Клапейрона-Клаузиуса справедливо для всех фазовых превращений, происходящих с поглощением или выделением теплоты.
Пример.
В случае плавления можно написать
,
где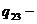 
удельная теплота плавления; 
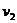и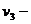 
удельные объемы жидкой и твердой фаз; 
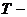температура плавления при давлении .
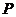Величина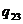 
существенно положительная, поэтому если
А)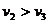 
, то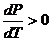 
. Это означает, что с повышением давления точка плавления повышается.
Б) 
, то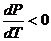 
. Тогда при повышении давления температура плавления понижается.
Случай Б) имеет место для воды.
Разность удельных объемов льда и воды при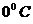 
приблизительно равна
;
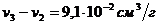удельная теплота плавления
.
Используя эти данные, получаем
.
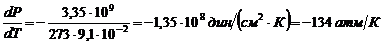Отсюда следует, что при увеличении давления на одну атмосферу точка плавления льда понижается приблизительно на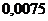 
градуса. Дьюар опытным путем получил 
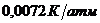, что хорошо согласуется с вычисленным значением.
Если на брусок льда, лежащий своими концами на неподвижных опорах, накинуть проволочную петлю и к ней подвесить тяжелый груз, то лед под проволокой