А. Решите задачу теории рядов.

МОсо

Задания для контрольной работы по математике

Для студентов 1 курса очной формы обучения

Направления «менеджмент»

(номер варианта – порядковый номер студента в списке группы)

Агарков Павел Юрьевич
Алексеев Дмитрий Викторович
Алферова Кристина Владимировна
Балыбин Олег Юрьевич
Быстрова Анастасия Павловна
Гершкул Сергей Дмитриевич
Дмитриева Алла Дмитриевна
Зинык Вита Михайловна
Кондрашова Кристина Александровна
Копейкина Светлана Николаевна
Кочетов Дмитрий Алексеевич
Курносов Андрей Дмитриевич
Латышева Наталия Александровна
Любавина Евгения Андреевна
Морозов Дмитрий Алексеевич
Мухортова Александра Викторовна
Панин Михаил Александрович
Плахотник Ольга Викторовна
Савельева Светлана Александровна
Сайдаров Минкаил Илесович

II семестр

А. Решите задачу теории рядов.

1.	Найти сумму ряда:	2.	Найти сумму ряда:
3.	Исследовать на сходимость ряд	4.	Исследовать на сходимость ряд
5.	Найти область сходимости ряда	6.	Найти область сходимости ряда
7.	Найти сумму ряда:	8.	Найти сумму ряда:
9.	Исследовать на сходимость ряд	10.	Исследовать на сходимость ряд
11.	Найти область сходимости ряда	12.	Найти область сходимости ряда
13.	Найти сумму ряда:	14.	Найти сумму ряда:
15.	Исследовать на сходимость ряд	16.	Исследовать на сходимость ряд
17.	Найти область сходимости ряда	18.	Найти область сходимости ряда
19.	Найти сумму ряда:	20.	Найти сумму ряда:
21.	Исследовать на сходимость ряд	22.	Исследовать на сходимость ряд
23.	Найти область сходимости ряда	24.	Найти область сходимости ряда
25.	Найти сумму ряда:	26.	Найти сумму ряда: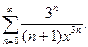
27.	Исследовать на сходимость ряд	28.	Исследовать на сходимость ряд
29.	Найти область сходимости ряда	30.	Найти область сходимости ряда

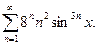
Б. Решите дифференциальное уравнение:

1.		2.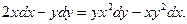
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.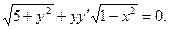
29.		30.

В. Решите дифференциальное уравнение высшего порядка:

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.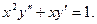
19.		20.
21.		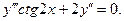22.
23.		24.
25.		26.
27.		28.
29.		30.

Г. Решите задачу, используя формулы комбинаторики:

1.	В профкоме имеются 3 туристические путевки. Сколькими способами их можно распределить среди 5 желающих сотрудников, если три путевки по трем разным маршрутам: Крым, Алтай, Карпаты?
2.	Некоторое число шахматистов приняло участие в турнире, причем каждые 2 шахматиста встречались 1 раз. Если бы число шахматистов было на 11 меньше, то число сыгранных партий в турнире уменьшилось в 12 раз. Сколько партий было сыграно в турнире?
3.	Сколькими способами из 35 учеников класса можно выбрать трех дежурных по школе и одного по столовой?
4.	Из некоторого числа кандидатов надо выбрать троих на три различных должности. Если бы кандидатов было на 2 меньше, то число возможных распределений работы уменьшилось бы в пять раз. Сколько было всего кандидатов?
5.	В подразделении 60 солдат и 5 офицеров. Сколькими способами можно выделить караул, состоящим из трех солдат и одного офицера?
6.	Из цифр 1,2,3,4,5 составляются пятизначные числа, не кратные 5 и не содержащие одинаковых цифр. Сколько существует таких чисел?
7.	В розыгрыше первенства страды по футболу в высшей лиге класса "А" участвует 10 команд. Команды, которые займут первое, второе и третье места, награждаются соответственно золотой, серебряной и бронзовой медалями, а команды, которые займут последние два места, покинут высшую лигу. Сколько разных результатов первенства может быть?
8.	На собрании должны выступить 4 человека А, В, С, D. Сколькими способами их можно разместить в списке ораторов, если В не может выступать до того момента, пока не выступит А?
9.	3 юноши и 7 девушек отправляются на двух лодках по реке. Сколькими способами их можно разместить в лодках поровну, чтобы в каждой был хотя бы один юноша?
10.	Курьеру поручено разнести пакеты в 6 различных учреждений. Сколько различных маршрутов он может выбрать?
11.	Из группы, состоящей из 7 мужчин и 4-х женщин, надо выбрать 6 человек. Сколькими способами это можно сделать так, чтобы среди них было а) не больше двух женщин; б) не менее двух женщин.
12.	Из букв АВСаЬс сколько можно составить перестановок, начинающихся с прописной буквы?
13.	Сколькими способами можно группу из 15 студентов разбить а) на 2 группы в б и 9 человек? б) на 3 группы в 3, 7 и 5 человек?
14.	В магазине имеется 5 сортов конфет. Сколько различных покупок, содержащих не более трех сортов конфет можно сделать в этом магазине? (Покупки считаются одинаковыми, если они состоят из одинаковых сортов конфет).
15.	Сколько различных трехзначных чисел можно составить из цифр 3,5,7. а) без повторения цифр в числе, б) цифры могут повторяться?
16.	Сколькими способами могут быть присуждены 1,2 и 3 премии трем лицам, если число соревнующихся равно 10?
17.	Сколько можно составить двузначных или трехзначных чисел из нечетных цифр при условии, что ни одна цифра не повторится.
18.	В классе 20 мальчиков и 20 девочек. Для участия в концерте нужно выделить танцующий дуэт, дуэт певцов и гимнастический дуэт (каждый из которых состоит из мальчика и девочки). Сколькими способами это можно сделать при условии, что все умеют петь, танцевать и выполнять гимнастические упражнения?
19.	Сколькими способами можно составить трехцветный флаг (три горизонтальные цветные полосы равной ширины), если имеется материал 5 разных цветов? Та же задача, если одна из полос должна быть красной (красным - один из имеющихся цветов).
20.	Сколько различных трехзначных чисел, меньших 400, можно составить из цифр 1,3,5,7,9 при условии, что цифры в числе не должны повторяться? Могут повторяться?
21.	Сколько существует различных положений, в которых могут оказаться 4 переключателя, если каждый из них может быть включен или выключен?
22.	Абоненту в библиотеке предлагают на выбор 3 книги и 3 журнала. Сколькими способами он может выбрать 3 экземпляра так, чтобы среди них было: а) обязательно 2 книги, б) не менее 2-х книг?
23.	Сколько перестановок можно сделать из букв слова "вершина" так, чтобы: а) "ш" стояло посередине? б) чтобы перестановка начиналась с "ш"? в) чтобы начиналась на " в", а кончалась на "на"?
24.	Сколько различных трехбуквенных "слов" можно составить из букв слова " ромб"?
25.	В 12-тиэгажном доме на первом этаже в лифт садятся 8 человек. Известно, что они выйдут группами в 1, 2, 5 человек на разных этажах. Сколькими способами они могут это сделать?
26.	У одного человека имеется 7 книг по математике, а у другого - 9. Сколькими способами они могут осуществить обмен книгу на книгу?
27.	У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен 300, а ребенку дают не более трех разных имен?
28.	Сколько различных полных обедов можно составить, если в меню имеется 3 первых, 4 вторых к 2 третьих блюда?
29.	Сколько можно получить различных четырехзначных чисел, вставляя пропущенные цифры в числа 25, 37?
30.	В 12-тиэтажном доме на первом этаже в лифт садятся 9 человек. Известно, что они выйдут группами в 2. 3, 4 человека на разных этажах. Сколькими способами они могут это сделать, если на 2-м этаже лифт не останавливается?

Д. Решите задачу по теории вероятностей:

1.	Ребенок играет с 10 бук нам и разрезной азбуки: А, А, А, Е, И, К, М, М, Т, Т. Какова вероятность того, что при ему чай ном расположении буки и ряд он получит слово МАТЕМАТИКА?
2.	Брошены три игральные кости. Чему равна вероятность того, что на одной из них выпала единица, если на всех грех костях выпали разные числа?
3.	Пусть вероятность попадания в цель равна 1/5. Производится 10 независимых выстрелов. Какова вероятность попадания в цель по меньшей мере дважды?
4.	Имеется 5 урн следующего состава: в первой и второй урнах по 2 белых и 3 черных шара в каждой; в третьей и четвертой урнах по 1 белому и 4 черных шара; в пятой урне 4 белых и 1 черный шар. Из одной наудачу выбранной урны взят шар. Он оказался белым. Чему равна при этом вероятность того, что шар вынут из пятой урны?
5.	В лифт 9-этажного дома на первом этаже вошли 5 человек. Известно, что каждый из них с равной вероятностью может выйти на любом из этажей, начиная со второго. Найти вероятность того, что все пятеро выйдут на разных этажах.
6.	Из колоды карт (З6 листов) последовательно вынуты две карты. Найти вероятность того, что вторая карта будет тузом, если первоначально был вынут туз.
7.	Вероятность получения удачного результата при проведении сложною химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если их общее число равно 7.
8.	При некоторых условиях стрельбы стрелок А поражает мишень с вероятностью p1 = 3/5, стрелок В с вероятностью р2 = 1/2, стрелок С - с вероятностью р3 = 2/5. Стрелки дали залп по мишени, и две пули попали в цель. Что вероятнее: попал С в мишень или нет?
9.	Колода игральных карт (52 листа, 4 масти по 13 карт в каждой) тщательно перетасована. Наудачу берут G карт (без возвращения). Описать пространство элементарных исходов, а также найти вероятность того, что среди этих карт окажется король пик.
10.	В ящике лежат 12 красных, 8 зеленых и 10 синих шаров. Наудачу вынимаются два шара. Какова вероятность того, что вынуты шары разного цвета, если известно, что среди них нет синего?
11.	Наблюдениями установлено, что в некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность того, что из восьми случайно взятых в этом месяце дней три дня окажутся дождливыми?
12.	Группа студентов, сдающая экзамен, состоит из 5 отличников, 10 хороших студентов и 15 слабых студентов; отличник всегда получает оценку «отлично», хороший студент — «отлично» и «хорошо» с равными вероятностями, слабый студент— «хорошо», «удовлетворительно» и «неудовлетворительно» с равными вероятностями. Какова вероятность, что наугад вызванный студент получит оценку «хорошо»?
13.	Десять рукописей разложены но 30 папкам (на одну рукопись приходится три папки). Найти вероятность того, что в случайно отобранных 6 папках не содержится целиком ни одна рукопись.
14.	В группе учатся 10 студентов. Для решении задачи у доски любого из них могут вызвать с равной вероятностью один раз в течение занятия. В группе три отличника. Найти вероятность того, что вторую задачу к доске пойдет решать отличник, при условии, что первую задачу тоже решал отличник.
15.	Батарея дала 14 выстрелов по объекту, вероятность попадания в который при каждом выстреле равна 1/5. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.
16.	Среди пациентов туберкулезного диспансера 15% принадлежат к первой категории больных, 66% ко второй и 19% к третьей. Вероятности возникновения заболевания, в зависимости от категории больных, равны соответственно 0,12, 0,09 и 0,2. Найти вероятность возникновения заболевания у наугад выбранного пациента диспансера.
17.	Из колоды карт (52 листа) наудачу вынимаются три карты. Найти вероятность того, что это будут тройка, семерка и туз (в любом порядке).
18.	Брошены две игральные кости. Какова вероятность того, что на первой кости выпало 4 очка, если известно, что на второй кости выпало больше очков, чем на первой?
19.	Вероятность попадания в цель при каждом выстреле из орудия равна 4/5. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20?
20.	Из урны, содержащей 3 белых и 2 черных шара, вынимаются наудачу два шара и перекладываются во вторую урну, содержащую 4 белых и 4 черных шара. Найти вероятность вынуть после этого из второй урны белый шар.
21.	Бросаются 4 игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.
22.	Из полной колоды карт (52 листа) вынимают сразу две карты. Одну из них смотрят она оказалась дамой. После этого две вынутые карты перемешивают и одну из них берут наугад. Найти вероятность того, что она окажется тузом.
23.	Спортивные общества А и В состязаются тремя командами. Вероятности выигрыша матчей команд общества А против соответствующих команд В можно принять соответственно равными 4/5 для первой (против первой В), 2/5 для второй (против второй В), 2/5 для третьей (против третьей В). Дли победы необходимо выиграть не менее двух матчей из трех (ничьих не бывает). Чья победа вероятнее?
24.	На склад поступила однотипная продукции с трех фабрик. Объемы поставок относятся соответственно как 2:5:3. Известно, что нестандартных изделий среди продукции первой фабрики 3%, второй - 2%, третьей - 1%. Найти вероятность того, что взятое наугад со склада изделие произведено первой фабрикой, если известно, что оно оказалось нестандартным.
25.	Какова вероятность того, что в четырехзначном номере случайно выбранного в большом городе автомобиля две пары одинаковых цифр.
26.	В кармане лежат 5 монет достоинством в 50 коп., 4 монеты по 10 коп. и 1 монета 5 коп. Наугад берут 3 монеты. Какова вероятность того, что в сумме они составляют не более одного рубля?
27.	Игрок А одновременно подбрасывает три игральные кости, а игрок Б в то же время - две кости. Эти испытания они проводят последовательно до первою выпадения «6» хотя бы на одной кости. Найти вероятность события А = {впервые «6» появилось у игрока А, а не у Б}.
28.	Предположим, что 5 мужчин из 100 и 20 женщин из 10000 являются дальтониками. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина?
29.	В ящике 10 красных и 6 синих пуговиц. Какова вероятность того, что две наудачу вынутые пуговицы будут одноцветными?
30.	Из полной колоды карт (52 листа) вынимают одновременно 7 карт. Одну из них смотрят она оказывается королем. После этого её перемешивают с остальными вынутыми картами. Найти вероятность того, что при втором вынимании карты из этих 7-ми снова получим короля.

А. Решите задачу теории рядов.

Поиск по сайту