Вид занятия: лекция № 11 (академическая: традиционная): «Параллельный колебательный контур»
Время: 2 часа ( 90 мин)
Место проведения: учебная аудитория
Категория обучающихся: студенты 3-го курса (очная форма обучения)
Воронеж ‑ 2015
Цели занятия:
а) образовательная (изучение; раскрытие; ознакомление; формирование знания, умения, навыков);
б) развивающая (формирование и развитие познавательного интереса учащихся к предмету; формирование и развитие самостоятельности; овладение основными способами мыслительной деятельности; развитие речи);
в) воспитательная (формирование и развитие инженерных, технических, экономических и других качеств личности).
Учебно-материальное обеспечение:
дидактический, иллюстративный и раздаточный материал по теме (мультимедийные презентации);
технические средства обучения (мультимедийный проектор, компьютер).
Метод(ы) обучения:
объяснительно-репродуктивный, репродуктивный, объяснение с иллюстрацией.
Учебные вопросы:
Расчет сложных цепей при гармонических воздействиях тригонометрическим методом; Векторное диаграммы в последовательном соединении сопротивления, индуктивности и емкости.
Основные понятия:
Комплексные величины, векторные диаграммы, сдвиг фаз.
Межпредметные связи:
основные сведения из физики, математики
Литература:
1. Бычков, Ю. А. Основы теории электрических цепей: учебник для вузов [Текст] / Ю. А. Бычков, В. М. Золотницкий, Э. П.Чернышев. – 3-е изд., стер. – СПб.: Издательство «Лань». – 2004.
2. Бакалов, В. П. Основы теории цепей, учеб. пособие для вузов, 2013.- гриф.
3. Попов, В. П. Основы теории цепей: учебник для вузов [Текст] / В. П. Попов. – 5-е изд. – М.: Высш. шк., 2005. – 574
| Ход занятия: | Время, мин. |
| 1. Вводная часть: приветствие; проверка явки и заполнение журнала; проверка готовности обучающихся к занятию; мотивационное обеспечение учебно-познавательной деятельности (установка на участие в работе; актуализация проблемы (знаний) и др.). Определение порядка работы на занятии и др. | 5 мин. |
| 2. Основная часть: Сообщение новых знаний преподавателем и усвоение их обучаемыми. | 75 мин. |
| 3. Подведение итогов проведенного занятия, ответ на вопросы обучаемых. Оценка работы обучающихся. | 5-7 мин. |
| 4. Формирование домашнего задания: постановка вопросов для самопроверки и перечня заданий из учебника. Цели домашнего задания: чтение учебной литературы (основной, дополнительной, справочной), конспектирование, решение задач, подготовка к экзамену, зачету. | 2-3 мин. |
| 5. Организационное завершение занятия (сбор раздаточного дидактического материала). | 2-3 мин. |
Параллельный колебательный контур
Контур с параллельным соединением G, L, C (рис. 1) дуален последовательному контуру.

Рис. 1
Поэтому изучать его свойства будем с использованием аналогии, вытекающей из принципа дуальности.
При частотах, близких к резонансной, ток в параллельных ветвях L и C высокодобротного контура значительно превышают ток входной ветви I; отношение IL0/I = IC0/I = Q.
Анализ работы контура при питании от источника напряжения U приводит к элементарным результатам: IG = UG; IL = U/wL; IC = UwC. Зависимости токов в ветвях контура от частоты имеют очевидный характер. Для общего тока имеем в этом случае I = Uy. Эта зависимость подобна кривой z(w.)
Рассмотренные свойства последовательного и параллельного колебательных контуров показывают, что подобные двухполюсники удобно использовать для фильтрации сигналов — подавления или выделения определенных частот путем настройки контура на эту частоту в качестве резонансной. При высокой добротности полное сопротивление последовательного контура, малое при частотах, близких к резонансной, резко возрастает при удалении от нее. Сопротивление высокодобротного параллельного контура, наоборот, весьма велико при резонансной и близких к ней частотах, и резко падает при удалении от резонансной частоты. Это позволяет осуществить ограничение сигнала данной частоты путем включения параллельных LC-звеньев последовательно в цепь прохождения тока к нагрузке и последовательных LC-цепочек параллельно сопротивлению нагрузки (рис. 2, а).

Рис. 2
При соблюдении условий в сопротивлении Rн ток частоты w0 будет отсутствовать.
Для решения противоположной задачи — выделения сигнала с частотой w0 из спектра частот — последовательные и параллельные контуры следует включить противоположным образом (рис. 2, б). Настройка обоих контуров на частоту w0 приводит к тому, что все сигналы, частота которых отличается от данной, будут ослабляться подобным фильтром.
Параллельный колебательный контур с потерями (рис. 3).

Рис. 3
Оценим, насколько зависят частотные свойства идеального параллельного LC-контура от потерь энергии в активных сопротивлениях элементов контура R1 и R2. Для определения резонансной частоты используем выражение комплексной проводимости контура
 =
=  ,
,
или

Его мнимая часть определяет реактивную проводимость  .
.
Из условия B = 0 найдем  . Отсюда следует, что при больших значениях R1 или R2, когда подкоренная дробь становится отрицательной, резонанс в цепи отсутствует. Это характерно для цепей с резистивными элементами, в которых наличие катушек и конденсаторов не гарантирует возникновения резонансного режима. В отличие от параллельного контура без потерь (R1 = R2 = 0), обладающего нулевой входной проводимостью на резонансной частоте, контур с потерями имеет ненулевую проводимость при резонансе, так как протекание тока в параллельных ветвях сопровождается потерями, которые должны покрываться источником во входной ветви.
. Отсюда следует, что при больших значениях R1 или R2, когда подкоренная дробь становится отрицательной, резонанс в цепи отсутствует. Это характерно для цепей с резистивными элементами, в которых наличие катушек и конденсаторов не гарантирует возникновения резонансного режима. В отличие от параллельного контура без потерь (R1 = R2 = 0), обладающего нулевой входной проводимостью на резонансной частоте, контур с потерями имеет ненулевую проводимость при резонансе, так как протекание тока в параллельных ветвях сопровождается потерями, которые должны покрываться источником во входной ветви.
В остальном частотная зависимость y(w) контура с потерями при высокой добротности 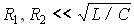 близка к частотной характеристике проводимости контура без потерь y(w) = ½1/(wL) – wC½, отличаясь от последней тем, что проводимость контура с потерями сохраняет конечное значение при нулевой и бесконечно большой частотах.
близка к частотной характеристике проводимости контура без потерь y(w) = ½1/(wL) – wC½, отличаясь от последней тем, что проводимость контура с потерями сохраняет конечное значение при нулевой и бесконечно большой частотах.
Наибольший практический интерес рассматриваемая цепь представляет при R2 = 0, поскольку активное сопротивление катушки существенно превышает активное сопротивление конденсатора. В этом случае резонансная частота равна  , а проводимость контура при резонансе y(w) = R1C/L. При высокой добротности эта величина достаточно мала, что позволяет использовать подобный контур для эффективного подавления нежелательных частот в рассмотренных выше схемах фильтрации сигналов (рис. 2).
, а проводимость контура при резонансе y(w) = R1C/L. При высокой добротности эта величина достаточно мала, что позволяет использовать подобный контур для эффективного подавления нежелательных частот в рассмотренных выше схемах фильтрации сигналов (рис. 2).
Подготовила:
преподаватель кафедры ОРЭ, к.ф.-м.н. _____________ Т. И. Касаткина