Проверяемые требования. Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы. Определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами.
Расстояние от точки до прямой – это длина перпендикуляра, опущенного на эту прямую.
В практических задачах мы сначала будем искать плоскость, которую определяют прямая и точка. Затем, в полученной плоскости строить перпендикуляр из точки на заданную прямую.
1. В правильной шестиугольной призме АВСDEFA1B1C1D1E1F1, все ребра которой равны 1. Найдите расстояние от точки С до прямой F1E1.
2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от точки С до прямой АВ1.
3. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от середины ребра AA1 до прямой BD1.
4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 4, найдите расстояние от точки A до прямой B1С1.
5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 10, найдите расстояние от точки E до прямой B1С1.
6. В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите расстояние от точки С до прямой BD1.
7. В кубе ABCDA1B1C1D1 все ребра равны 1. Найдите расстояние от точки C до AD1.
8. Дан куб АВСDA1B1C1D1 с ребром 2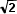 
. Найдите расстояние от середины ребра В1С1 до прямой МТ, где точки М и Т – середины ребер AD и А1В1 соответственно.
9. Дан куб АВСDA1B1C1D1 с ребром 
. Найдите расстояние от середины ребра А1В1 до прямой МТ, где точки М и Т – середины ребер AD и CD соответственно. Ответ: 3.
10. В единичном кубе ABCDA1B1C1D1 на диагоналях AD1 и D1B1 взяты точки E и F, так то D1E =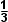 
AD1, D1F = 
D1B1. Найдите расстояние от точки D1 до прямой EF.
11. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки В до прямой АС1.
12. В правильной треугольной призме ABCA1B1C1 высота равна 2, сторона основания равна 1. Найдите расстояние от точки В1 до прямой АС1.
13. Задача полностью подобная предыдущей. На чертеже изменила только буквы... В правильной треугольной призме ABCA1B1C1 высота равна 1, а ребро основания равно 2. Найдите расстояние от точки А1 до прямой ВС1.
14. В тетраэдре ABCD, все ребра которого равны 1, найдите расстояние от точки A до прямой, проходящей через точку B и середину E ребра CD.
15. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой, равны 1, а боковые ребра равны 2, найдите расстояние от точки C до прямой SA.
16. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой, равны 1, а боковые ребра равны 2, найдите расстояние от точки C до прямой SF.
17. Дана правильная четырехугольная пирамида SABCD с вершиной S. Ребро основания пирамиды равно , высота – 
. Найдите расстояние от середины ребра AD до прямой MT, где M и T – середины ребер CS и BC соответственно.
18. Дана правильная треугольная пирамида DABC с вершиной D. Ребро основания пирамиды равно , высота – 
. Найдите расстояние от середины ребра BD до прямой MT, где M и T – середины ребер AC и AB соответственно.
19. Дана правильная треугольная пирамида DABC с вершиной D. Боковое ребро пирамиды равно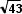 
, высота равна 
. Найдите расстояние от середины бокового ребра BD до прямой МТ, где точки М и Т — середины ребер АС и AD соответственно. Ответ: 3