Это средство реализует критерий проверки гипотезы о равенстве (неравенстве) математических ожиданий распределений двух независимых генеральных совокупностей (малые независимые выборки), имеющих нормальные распределения с неизвестными дисперсиями в предположении, что дисперсии равны. Этот критерий, называется t -тестом или тестом Стьюдента.
Рассмотрим выходные данные, вычисляемые этим средством, на примере проверки нулевой гипотезы Но: μ1 - μ2 = δ (δ задано) против разных конкурирующих гипотез: Н1: μ1 ≠ μ2 + δ или Н1: μ1 > μ2 + δ, либо Н1: μ1 < μ2 + δ (μ1 и μ2— неизвестные математические ожидания выборок). Исходные данные и заполненное диалоговое окно Двухвыборочныи t-тест с одинаковыми дисперсиями показаны на рис.23а. Выборки извлечены из нормально распределенных генеральных совокупностей с одной и той же дисперсией, равной 1, и математическими ожиданиями 0 и 1 соответственно[2]. Проверим гипотезу, что μ1 - μ2 = 2 (на самом деле μ1 - μ2 = 1).
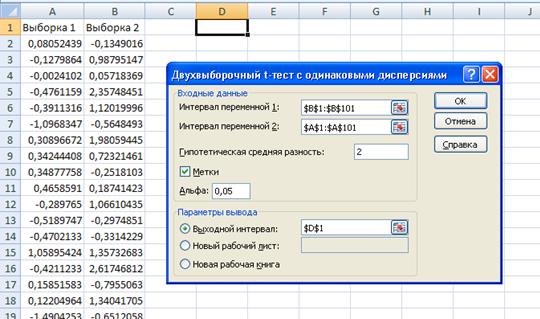
Рис. 2.3а. Исходные данные и диалоговое окно Двухвыборочныи t-mecm с одинаковыми дисперсиями
Отметим, что средство требует, чтобы δ, значение которого задается в поле Гипотетическая средняя разность, было неотрицательно. Поэтому первым (в поле ввода Интервал переменной 1) задается адрес диапазона ячеек, содержащий выборку с большим математическим ожиданием, а затем в поле Интервал переменной 2 указывается адрес второй выборки. (Диапазоны должны состоять из одного столбца или одной строки.) В поле Альфа вводится значение уровня значимости α.
Для удобства анализа результатов сформируем исходные данные таким образом, чтобы выборка с большим математическим ожиданием расположилась в первом столбце. В нашем примере необходимо поменяем местами исходные выборки. Итак, имеем две выборки объемом по 100 значений каждая, показанные на рис. 2.3б. Выборки имеют одинаковую дисперсию, равную 1, и математическими ожиданиями 1 и 0 соответственно. Результат вычислений средства Двухвыборочныи t-тест с одинаковыми дисперсиями показан на рис.2.4.
|
|
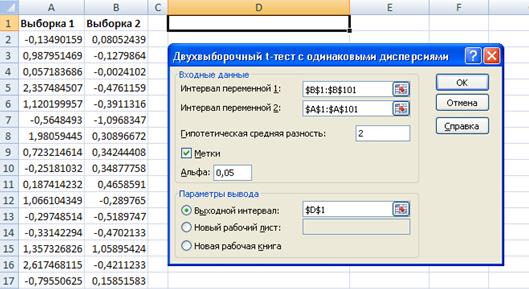
Рис. 2.3б. Исходные данные и диалоговое окно Двухвыборочныи t-mecm с одинаковыми дисперсиями
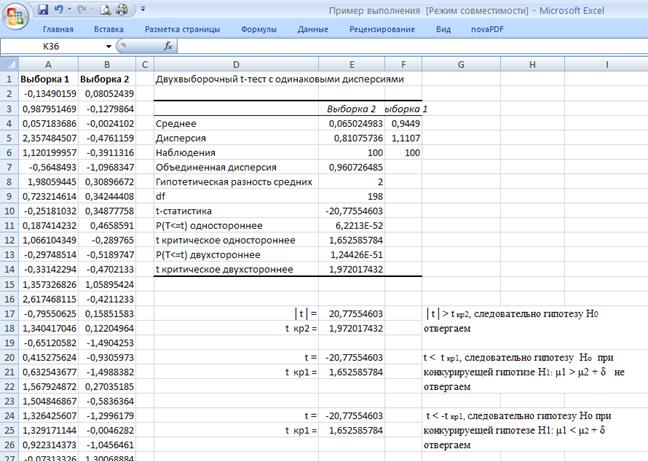
Рис.2.4. Результат вычислений
В итоговой таблице приводятся следующие данные.
• Среднее — выборочные средние для каждой выборки.
• Дисперсия — несмещенные выборочные оценки дисперсий выборок.
• Наблюдения — объемы выборок.
• Гипотетическая разность средних — значение δ, которое задано в диалоговом окне.
• Объединенная дисперсия — "средняя" оценка дисперсии; рассчитывается по формуле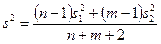 
, где п и т — объемы выборок, si2 — оценки дисперсий (их значения приводятся в строке Дисперсия).
• df — число степеней свободы; вычисляется как (п + т - 2).
• t-статистика — значение критериальной статистики; вычисляется по формуле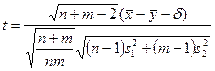 
, имеет распределение Стьюдента с df степенями свободы.
• P(T<=t) одностороннее — вероятность P(X ≤ t), где X — случайная величина, имеющая распределение Стьюдента с df степенями свободы, t — подсчитанное значение критериальной статистики.
• t критическое одностороннее — значение квантиля tкр1 порядка (1 – α) распределения Стьюдента с df степенями свободы.
• P(T<=t) двухстороннее — вероятность Р(|Х|<|t|), где X — случайная величина, имеющая распределение Стьюдента с df степенями свободы, t — подсчитанное значение критериальной статистики.
|
|
• t критическое двухстороннее — значение квантиля tкp2 порядка (1 - а/2) распределения Стьюдента с df степенями свободы.
Нулевая гипотеза Но: μ1 - μ2 = δ принимается, если \t\ < tкp2 (в противном случае отвергается); гипотеза Но при конкурирующей гипотезе Н1: μ1 > μ2 + δ принимается, если t < tкp1; при конкурирующей гипотезе Н1: μ1 < μ2 + δ нулевая гипотеза принимается при выполнении неравенства
t > - tкp1 .
Как видно из результатов расчета, в данном примере нулевую гипотезу Но: μ1 - μ2 = δ следует отвергнуть при конкурирующей гипотезе о неравенстве μ1 - μ2 ≠ δ и конкурирующей гипотезе H1: μ1 < μ2 + δ. При конкурирующей гипотезе H1: μ1 > μ2 + δ нулевую гипотезу Но: μ1 - μ2 = δ нет оснований отвергать.
Статистическая функция ТТЕСТ при значении аргумента Тип = 2 вычисляет вероятности P(T<=t) двухстороннее и P(T<=t) одностороннее.