Предмет: геометрия
Тема: «Теорема Пифагора»
Тип урока: изучение и первичное закрепление новых знаний и способов деятельности
Участники: обучающиеся 8 класса
Цель урока: Организовать деятельность учащихся для выведения, доказательства и первичного закрепления теоремы Пифагора
Планируемый результат обучения, в том числе и формирование УУД:
Предметные:
Знать теорему Пифагора.
Понимать, как найти неизвестную сторону прямоугольного треугольника при помощи теоремы Пифагора.
Познавательные УУД:
умение ориентироваться в своей системе знаний:отличать новое от уже известного; с помощью учителя добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Коммуникативные УУД: умениеоформлять свои мысли в устной форме;слушать и понимать речь других;
Регулятивные УУД: умение определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
Личностные УУД: способность к самооценке на основе критерия успешности учебной деятельности.
Основные понятия: Теорема Пифагора
Ресурсы: -Учебник для общеобразовательных учреждений: «Геометрия 7-9 класс» Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др
- презентация к уроку
- карточки для рефлексии
-карточки с задачами
-веревка с узелками
| Этапы урока | Содержание учебного материала. Деятельность учителя | Деятельность обучающихся | Формирование УУД | |||||||||||||||||||||||||||||||||||||
| Организационный момент | Приветствие, психологический настрой на урок | Настраиваются на урок, проверяют готовность своего рабочего места | ||||||||||||||||||||||||||||||||||||||
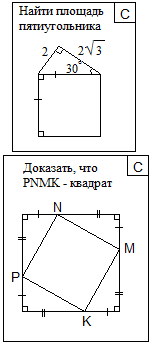
| Актуализация знаний | Задает вопросы по ранее изученному материалу (слайд3-9) 1.Какой треугольник вы видите на рисунке? 2.Какой треугольник называется прямоугольным? 3. Как называются стороны прямоугольного треугольника? 4.Что называется гипотенузой? 5.Что называется катетами? 6.Назовите свойства прямоугольного треугольника. 7.Сформулируйте свойства равенства прямоугольных треугольников. 8.Сформулируйте свойства равенства прямоугольных треугольников 9.Вспомните свойства площадей многоугольников. 10.Найдите площадь квадрата со стороной 6, 7,с, а, а+в 11. А как найти площадь прямоугольного треугольника? 12.Найдите сторону треугольника АС, если АВ = 12 см, а угол В = 300 13.Найти АВ, если АС = 4см, а угол А =600. 14.Найти АВ если ВС = 4 см, АС = 3 см. А С В | 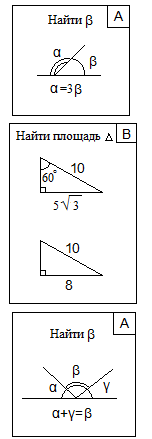 Решение задач по карточкам (наиболее подготовленные учащиеся) Решение задач по карточкам (наиболее подготовленные учащиеся)
| Отвечают на вопросы учителя. | Решают задачи как на доске, так и в тетрадях. | Уметь оформлять свои мысли в устной форме (Коммуникативные УУД). Уметь ориентироваться в своей системе знаний:отличать новое от уже известного с помощью учителя (Познавательные УУД). | |||||||||||||||||||||||||||||||||||
| Постановка проблемы | Создание проблемной ситуации. Предлагает решить последнюю задачу. (слайд 9). Использует побуждающий от проблемы диалог Вы смогли выполнить последнее задание? Что не получается? Чем это задание не похоже на предыдущее? Какой возникает вопрос? Проблема: Невозможно найти сторону АВ. Почему? Как вы думаете, какова цель нашего урока? Цель: научиться находить третью сторону прямоугольного треугольника, если известны две другие. (запишите в тетрадь) | Отвечают на вопросы учителя, принимают участие в диалоге. Выявляют место затруднения. Проговаривают причину. -ответы учащихся: научиться находить стороны прямоугольного треугольника Записывают цель в тетрадь | Уметь определять и формулировать цель на уроке с помощью учителя (Регулятивные УУД). постановка и формулирование проблемы, самостоятельное создание алгоритмов деятельности при решении проблем творческого и поискового характера; (познавательные УУД) | |||||||||||||||||||||||||||||||||||||
| Изучение новых знаний и способов деятельности | Создание учебной ситуации для разрешения данной проблемы.
Практическое задание:
Начертите в тетрадях прямоугольный треугольник с катетами,
1ряд -3и 4, 2ряд- 6и 8, 3ряд-5и12, измерьте гипотенузу и заполните таблицу
сравните сумму квадратов катетов с квадратом гипотенузы. Сделайте вывод: в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Это утверждение и есть теорема. (гипотеза) Но первоначально теорема Пифагора формулировалась так (слайд11) Еще раз сформулируем теорему Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Докажем теорему (слайд14) Постройте прямоугольный треугольник с катетами а и в, гипотенузой с. А в а
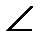 С=90 С=90 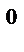 ; ;
ВС=а;
Док-ть:
Доказательство: Достроим прямоугольный треугольник до квадрата со стороной а+в. Достроим его до квадрата со стороной а+в.
Чтобы лучше запомнить теорему послушайте стихотворение И.Дырченко «Теорема Пифагора» (слайд15) Треугольник со сторонами 3,4 и 5 называется египетским. Для построения прямого угла использовали веревку длиной 12ед измерения, которая узлами была разделена на 3,4и 5 частей (слайд1,веревка) Считалось, что при закладке пирамид, процедуру определения прямых углов выполнял сам фараон.
Мы достигли цель, которую ставили в начале урока?
| Выполняют задание Ответы учащихся Обучающиеся в тетрадях записывают число и тему урока. Предлагают варианты доказательства Записывают доказательство в тетрадь | планирование учебного сотрудничества с учителем и сверстниками — определение цели, постановка вопросов — инициативное сотрудничество в поиске и сборе информации; — выявление, идентификация проблемы, поиск и оценка альтернативных способов разрешения умение с достаточной полнотой и точностью выражать свои мыслив соответствии с задачами и условиями коммуникации; (коммуникативные УУД) | |||||||||||||||||||||||||||||||||||||
| Закрепление изученного материала | Давайте закрепим полученную информацию на практике, решим задачу, предложенную в начале урока Решение задач (слайд16-17); для сильных учащихся слайд(19-21) №1. Найдите гипотенузу прямоугольного треугольника по данным катетам: a= 3 см, b=4 см. №2. Найдите катет прямоугольного треугольника по катету и гипотенузе: а=12см, с=13см. Зачем нам нужна теорема Пифагора? Для того чтобы находить стороны прямоугольного треугольника. Цель: научиться применять теорему Пифагора в различных задачах. Решение задач С помощью теоремы Пифагора можно решать два вида задач: 1.Найти гипотенузу прямоугольного треугольника, если известны катеты. 2. Найти катет, если известна гипотенуза и другой катет Решение задач из учебника: № 483(а, б), 484(а, б). | Работают в парах, записывают решение в тетрадь Ответы учащихся (устная работа) Формулируют новую цель Индивидуальная работа учащихся | поиск и выделение необходимой информации, в том числе решение рабочих задач с использованием общедоступных инструментов ИКТ и источников информации; структурирование знаний; осознанное и произвольное построение речевого высказывания в устной и письменной форме; выбор наиболее эффективных способов решения задач в зависимости от конкретных условий; ((познавательные УУД) | |||||||||||||||||||||||||||||||||||||
| Информация о домашнем задании | Запишите домашнее задание: п.54, вопр 8, №483(в),484(в),485,486(а) (выберите не менее двух № из четырех); исследование «Почему теорема Пифагора называется теоремой невесты или нимфы», найти другие способы доказательства. Кто желает получить дополнительную отметку может взять решить старинные задачи. | Записывают домашнее задание | ||||||||||||||||||||||||||||||||||||||
| Подведение итогов учебного занятия | - Давайте подведём итог нашей работы на уроке. С какой проблемой столкнулись на уроке? Какую цель поставили вначале урока? Достигли мы цели? Каким образом мы достигли цель? Разрешили проблему? Как вы думаете, какая цель будет на следующем уроке? | Отвечают на вопросы учителя. | ||||||||||||||||||||||||||||||||||||||
| Рефлексия учебной деятельности | Организует рефлексию и самооценку учениками собс2твенной учебной деятельности.
| Отвечают на вопросы учителя. Делают самооценку | Уметь оценивать правильность выполнения действия. (Регулятивные УУД). Способность к самооценке на основе критерия успешности учебной деятельности (Личностные УУД). | |||||||||||||||||||||||||||||||||||||
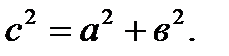
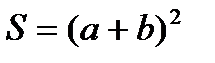 - площадь квадрата
- площадь квадрата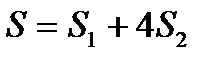
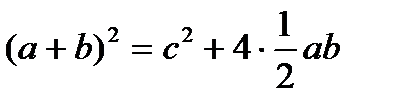
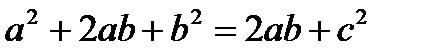
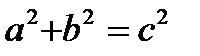 - теорема доказана.
- теорема доказана.