Общие теоретические сведения

ЛАБОРАТОРНАЯ РАБОТА № 4. ИССЛЕДОВАНИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ АКТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО СОПРОТИВЛЕНИЙ. РЕЗОНАНС НАПРЯЖЕНИЙ

Цель работы: Исследование явления резонанса напряжений, построение резонансных кривых и векторных диаграмм.

Общие теоретические сведения

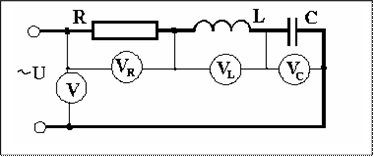
При исследовании электрической цепи, представленной на рис.4.1 следует иметь в виду, что ток в любом элементе схемы один и тот же, а питающее напряжение, согласно второму закону Кирхгофа, равно алгебраической сумме мгновенных значений напряжений на отдельных элементах схемы:

(4.1)

или в комплексной форме записи:

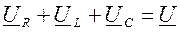(4.2)

 

 

Рис.4.1. Цепь переменного тока с последовательно включенными активным, индуктивным и емкостным сопротивлениями.

Падение напряжения на активном сопротивлении R совпадает по фазе с током . Падение напряжения на индуктивном сопротивлении X_L опережает ток на 90^о, а падение напряжения на емкостном сопротивлении X_C отстает от тока на 90^о. Таким образом, напряжения и всегда направлены на встречу друг другу. На рис. 4.2 приведены векторные диаграммы напряжений и токов схемы рис. 4.1 для различных значений X_С и X_L.

 

Рис.4.2 Векторные диаграммы электрической цепи с последовательным соединением элементов R,L,C: а) X_L>X_C; б) X_L=X_C; в) X_L<\X_C.

Векторные диаграммы строятся следующим образом. Поскольку через все элементы цепи проходит один и то же ток, то для упрощения построения в качестве исходного вектора принимают вектор тока . Под углом 90^о в сторону опережения по отношению к току откладывают вектор . Далее откладывают вектор по направлению вектора тока , и, наконец, под углом 90^о в сторону отставания по отношению к току откладывают вектор . Вектор питающего напряжения - это сумма трех векторов , и . По правилу замкнутого многоугольника вектор, проведенный из начала первого вектора к концу последнего вектора является результирующим вектором , составляющим угол j с током . Угол j на этой диаграмме это одновременно и начальная фаза напряжения и угол сдвига фаз между напряжением и током. Действительно, поскольку начальная фаза тока равна нулю, т.е. , то .

Из векторной диаграммы действующее значение приложенного напряжения определяется:

.

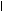
Отсюда ток

, (4.3)

где

называют полным сопротивлением цепи. Сдвиг по фазе между напряжением и током определяется

(4.4)

или

(4.5)

Если X_L > X_C, то U_L > U_C и угол j больше нуля. Eсли X_L < X_C, то U_L < U_C и угол j меньше нуля. Если же X_L = X_C, то U_L = U_C. Ток совпадает по фазе с напряжением , угол j = 0, cos j = 1 и этот режим называется резонансом напряжений.

При резонансе напряжений U_L = U_С. Это возможно, если x_L = x_C или wL = 1/ wC. В этом случае индуктивное сопротивление компенсирует емкостное сопротивление. В результате реактивное сопротивление X = X_L - X_C = 0 и реактивная мощность на зажимах цепи будут равны нулю. Полное сопротивление цепи Z в этом случае минимальное и равно активному сопротивлению R. Ток в цепи достигает максимального значения I _мax = U / R.

В цепи наблюдаются колебания энергии между емкостью и индуктивностью. От источника энергии потребляется только активная мощность, которая покрывает потери в активном сопротивлении при обмене электрической энергии конденсатора и индуктивности. Эта энергия переходит в тепло.

Резонанса напряжений можно достичь, изменяя индуктивность L (), емкость С () или угловую частоту (). Величина реактивного сопротивления контура при резонансе напряжений будет равна:

(4.6)

называют волновым сопротивлением цепи, а отношение волнового сопротивления к активному сопротивлению называют добротностью Q резонансного контура:

(4.7)

Напряжения на индуктивности и емкости определяются при резонансе

; (6.8)

Широкое применение резонанс напряжений нашел в радиотехнике, автоматике, телемеханике и связи для настройки приемных и передающих устройств на определенную частоту.

В силовых цепях последовательное соединение L и С применяется для уменьшения падения напряжения в линиях. В этом случае емкостное сопротивление x_C компенсирует индуктивное сопротивление линии x_L и падение напряжения в линии значительно уменьшается. Полное сопротивление линии становится минимальным и равным активному сопротивлению. Такой способ компенсации индуктивного сопротивления и реактивной мощности называют продольной компенсацией.

Однако следует помнить, что если в силовых цепях возникает непредусмотренный режим резонанса напряжений и X_L = X_C >> R (контур обладает большой добротностью Q), то U_C = U_L >> U, то в схеме возможны перенапряжения, которые могут вызвать пробой изоляции и в некоторых условиях - угрозу для жизни людей

При проведении опытов следует иметь ввиду, что сопротивление R - это активное сопротивление обмотки катушки индуктивности L. Поэтому вольтметр U_K замеряет не напряжение U_L, а напряжение на катушке U_K, которое равно U _К = U _R + U _L или для действующих значений:

(4.9)

Порядок выполнения работы

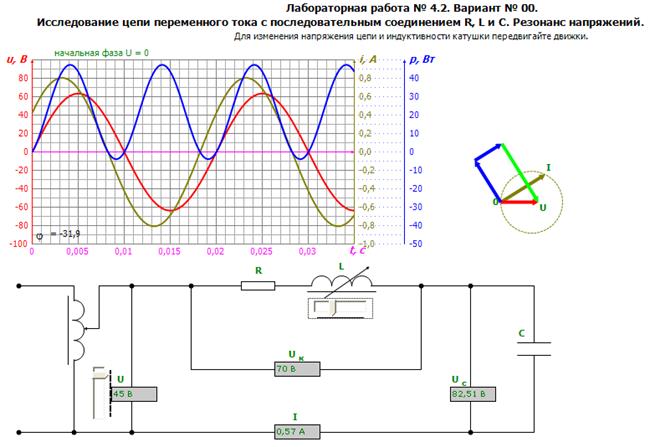
1.Выбрать в меню работу «4.1. Резонанс напряжений (начальная фаза тока =0)». В данной лабораторной работе исследуется режим резонанса напряжений при изменении индуктивного сопротивления X_L. Схема электрической цепи представлена на рис.4.3. Напряжение на входе схемы и параметры элементов схемы установлены компьютером в соответствии с шифром студента.

2. При постоянной емкости С конденсатора изменять величину индуктивности катушки от минимума до максимума. Изменение индуктивности катушки достигается перемещением движка. Выполнить 9 измерений: 4 измерения до резонанса, одно измерение при резонансе и 4 измерения после резонанса. Результаты девяти измерений записать в таблицу 4.1.

3. Проанализировать на экране дисплея как изменяется ток и мгновенная мощность, а также векторная диаграмма цепи.

Таблица 4.1

№ п/п	Измерено	Вычислено
U	I	UK	UC	P	R	ZK	XL	XC	Z	UL	cosj
В	А	В	В	Вт	Ом	Ом	Ом	Ом	Ом	В	-
		0,251	16,8	36,37	4,2211				144,9004	159,3626		0,4204
		0,348	29,4	50,42	8,1139		84,4828	51,4621	144,8851	114,9426	17,9088	0,5829
		0,507	62,2	73,34	17,2223		122,6825	102,7716	144,6548	78,8955	52,1052	0,8493
		0,571	80,7	82,67	21,8448		141,3309	124,4404	144,7811	70,0525	71,0555	0,9565
		0,597	95,2	86,42	23,8794		159,4639	144,7057	144,7571	67,0017	86,3893
		0,55	102,1	79,63	20,2675		185,6364	173,1239	144,7818	72,7273	95,2182	0,9213
		0,493	99,5	71,33	16,2843		201,8256	190,3801	144,6856	81,1359	93,8574	0,8258
		0,407	92,3	58,92	11,0985		226,7813	216,6582	144,7665	98,2801	88,1799	0,6817
		0,22	70,6	31,81	3,2428		320,9091	313,8369	144,5909	181,8182	69,0441	0,3685

 

Расчетные формулы: ; ; ,

I_max – максимальное значение тока в момент резонанса напряжений;

; ; ; .

 

 

Рис.4.3. Вид активного окна лабораторной работы №4.1. Принципиальная схема, волновые и векторные диаграммы цепи R,L,C, при условии, что начальная фаза тока равна нулю. Угол сдвига фаз φ>0.

Примечание. При выполнении лабораторной работы начальная фаза тока была принята за ноль, а изменялась начальная фаза напряжения. В действительности же неизменной остается начальная фаза питающего напряжения, а начальная фаза тока изменяется. Чтобы посмотреть, как изменяются начальные фазы в этом случае, нужно запустить программу лабораторной работы «4.2. Резонанс напряжений (начальная фаза напряжения =0)» (рис.4.4).

 

 

 

Рис.4.4. Вид активного окна лабораторной работы №4.2. Принципиальная схема, волновые и векторные диаграммы цепи R,L,C, при условии, что начальная фаза напряжения равна нулю. Угол сдвига фаз φ>0.

4. Результаты расчетов занести сначала для проверки в таблицу 4.2 в компьютере (вызвав ее из меню), а затем в такую же таблицу в отчете;

Таблица 4.2

№ п/п			C		Q
Ом	Ом	мкФ	Ом	_
		51,4621	61,8846
		102,7716	30,9883
		124,4404	25,5923
		144,7057	22,0082
		173,1239	18,3956
		190,3801	16,7281
		216,6582	14,6993
		313,8369	10,1477
Ответ			22,3333

 

5 Построить векторные диаграммы в одном масштабе по указанию преподавателя для трех случаев: X_L > X_C ; X_L = X_C; X_L < X_C.

Величины напряжений определяются:

U_R = RI; U_L = X_LI; U_C = X_CI; U _К= U _R + U _L; U = U _К+ U _R + U _L.

6 Построить резонансные кривые I; U_L; U_C; cos j; P; Z = f X_L).

Объяснить характер полученных кривых.

7 Сделать заключение по результатам работы.

Контрольные вопросы

1. Дать определение режима резонанса напряжений.

2. Сформулировать условие резонанса напряжений.

3. Как выражается Z при последовательном соединении R, L, C. Чему равно Z при резонансе?

4. Как изменяется Z при увеличении индуктивности цепи от 0 до ¥ при w = const и C = const?

5. Начертить кривые U_C; U_L; I = f (X_L).

6. Как влияет величина активного сопротивления R на характер резонансных кривых?

7. При каком соотношени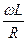и и напряжение источника питания при резонансе меньше U_L и U_С?

8. Как определить угол сдвига фаз между током и общим напряжением, зная U_K; U_С; U?

9. Построить векторную диаграмму цепи для режимов:

а) до резонанса; б) после резонанса; в) при резонансе.

10. Где применяется резонанс напряжений в технике?

11. Чему равно питающее напряжение U (рис.4.5), если известно, что U_R =30 В,. U_L =50 В, U_C =90 В?

 

 

Рис.4.5. Неразветвленная электрическая цепь содержащая R, L, C.

12. В электрической цепи рис. 4.5. известно: U = 50 B, U_С = 20 B, U_R = 30 B. Определить U_L.

13. Определить U_R, U_L, U_C и I при резонансе напряжений (рис.4.5), если U = 220 B, R = 22 Ом, X_L = 200 Ом.

14. В схеме (рис.4.6) существует резонанс напряжений. Даны показания приборов: U =30, В U_С =40 В. Чему равно показание U_К вольтметра V_к на активном сопротивлении и катушке?

 

 

Рис.4.6. Определение напряжения на катушке индуктивности в резонансном контуре R, L, C.