Графический метод решения ЗЛП

Л3. Методы решения задач линейного программирования

Наиболее простым и наглядным методом решения ЗЛП является графический метод. Он применим для решения ЗЛП с двумя переменными. На плоскости х₂0х₁ строится многоугольник решений АBCDEF:

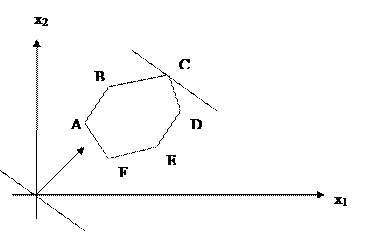
Рис.1

Среди точек этого многоугольника надо найти такую, в которой линейная функция F = c₁x₁+ c₂x₂ принимает максимум (минимум).

Рассмотрим линию уровня линейной функции F, т.е. линию, вдоль которой функция F принимает фиксированное значение С:

c₁x₁ + c₂x₂ = С. (1)

Примерами линий уровня являются линии постоянной температуры (изотермы) на картах прогноза погоды, параллели (линии уровня широты) и меридианы (линии уровня долготы) на географической карте.

Пусть надо найти самую северную точку страны. Это будет точка, имеющая наибольшую широту, т.е. точка, через которую проходит параллель с самой большой широтой. Именно так надо поступать при геометрическом решении ЗЛП. На многоугольнике решений ищется точка, через которую проходит линия уровня с наибольшим значением, если ищется максимум целевой функции.

Линии уровня (1) представляют собой параллельные прямые при различных значениях С, т.к. их угловой коэффициент определяется только соотношением между с₁ и с₂. Другими словами, линии уровня – это своеобразные параллели, расположенные под углом к осям координат.

При смещении линии уровня в одну сторону уровень только возрастает, а при смещении в другую – только убывает. Направление наибольшего возрастания функции показывает вектор-градиент, координаты которого равны частным производным функции:

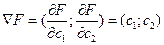. (2)

Градиент ориентирован перпендикулярно линиям уровня.

Если провести линию уровня через ноль и перемещать ее параллельно самой себе в направлении градиента, то можно найти точку максимума целевой функции подобно тому, как на географической карте находится самая северная точка.

Таким образом, графический метод решения ЗЛП сводится к следующим этапам:

1. На координатной плоскости х₂0х₁ строится многоугольник решений.

2. Находится градиент целевой функции .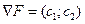

3. Линия уровня c₁x₁ + c₂x₂ = С, перпендикулярная градиенту, передвигается в его направлении до тех пор, пока не покинет пределы многоугольника решений. Предельная точка этого движения и является точкой максимума целевой функции.

4. Для нахождения координат точки максимума решается система двух уравнений, описывающих пересекающиеся в этой точке прямые.

В случае минимизации целевой функции линию уровня надо передвигать в направлении, противоположном направлению градиента.

При графическом решении ЗЛП возможны случаи, когда область допустимых решений системы ограничений представляет пустое множество (условия задачи противоречивы) или не ограничена. В этих случаях оптимального решения не существует.

Пример 1. Мебельный цех выпускает изделия двух типов Т₁ и Т₂. На каждое изделие типа Т₁ расходуется 1 единица ресурса Р₁, 1 единица ресурса Р₂ и единица ресурса Р₃. На каждое изделие типа Т₂ расходуется 1 единица ресурса Р₁ и 4 единицы ресурса Р₂. Ресурсы мебельного цеха ограничены: в день можно расходовать не более 8 единиц ресурса Р₁, 20 единиц ресурса Р₂ и 5 единиц ресурса Р₃. Какое количество изделий типа Т₁ и Т₂ должен выпускать цех ежедневно, чтобы обеспечить максимальную прибыль, если прибыль от реализации изделия Т₁ – 1 денежная единица, а от реализации Т₂ – 2 денежные единицы.

Решение

Введем обозначения: х₁ – число изделий типа Т₁; х₂ – число изделий типа Т₂. Прибыль от реализации изделий Т₁ составляет х₁, а от реализации изделий типа Т₂ - 2х₂, т.е. необходимо максимизировать целевую функцию:

F = x₁ + 2x₂ → max.

Ограничения задачи имеют вид:

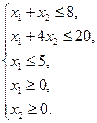
Первому ограничению соответствует прямая, проходящая через точки (0;8) и (8;0) (рис.2).

Рис.2

Второму ограничению соответствует прямая, проходящая через точки (0;5) и (20;0).

Решением неравенства х₁≤ 5 (ограничение по количеству изделий типа Т₁) является полуплоскость, лежащая слева от прямой х₁ = 5. Таким образом, область допустимых решений ЗЛП представляет собой пятиугольник.

Для определения направления движения к оптимуму построим вектор – градиент 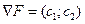= (1;2). При максимизации целевой функции следует двигаться в направлении вектора 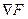. В крайней угловой точке этого движения (точка А на рис.2) достигается максимум целевой функции.

Для нахождения координат точки А достаточно решить систему уравнений соответствующих прямых:

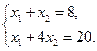
Отсюда легко получается решение ЗЛП: максимум целевой функции F = 12 достигается при х₁ = 4 и х₂ = 4.

Графический метод решения ЗЛП прост, нагляден, позволяет быстро и легко получить ответ. Однако он неприемлем для решения практических задач, т.к. его можно применять только в том случае, когда число переменных в стандартной задаче равно двум, или когда ЗЛП в канонической форме удовлетворяет условию n – r = 2, где n – число неизвестных задачи, r – ранг матрицы системы ограничений.

Поэтому необходимы аналитические методы, позволяющие решать ЗЛП с любым числом переменных.