Метод средней точки (метод Больцано)
Данный метод является вариантом метода деления интервала пополам. Последовательные сокращения интервала неопределенности производятся на основе оценки производной минимизируемой функции в центре текущего интервала.
Начальный этап. Для запуска метода необходимо:
(1) задать [a1,b1]- начальный интервал локализации минимума, на границах которого знаки производных различны, т.е. f'¢(a1)f'¢(b1)<0; e - малое положительное число;
(2) положить к=1 и перейти к основному этапу.
Основной этап
Шаг 1. Взять пробную точку хk в центре текущего интервала и проверить критерий окончания поиска: (1) xk = (ak + bk)/2; (2) если ½f'¢(xk)½ ≤ e и Lk= ½bk - ak½≤ e, то остановиться (хk = х* -аппроксимирующий минимум).
Шаг 2. Сократить текущий интервал:
(1) Если f ¢(xk) > 0, то положить ak+1 = ak и bk+1 =xk, в противном случае - ak+1 =xk, bk+1 =bk;
(2) заменить k на k+1 и вернуться на шаг 1.
Метод ДСК:
Интерполяционный метод нахождения минимума
Начальный этап:
1) задать x0 – произвольная начальная точка.
2) выбрать шаг h равным 0.01…0.001(если x0 = 0) или 0.01*|x0|(если x0 не = 0).
3) e1=e2 (0.01…0.001)
Основной этап:
Шаг 1:
Получить 3 равностоящих точки методом Свенна2:
1) Установить направление убывания целевой функции. Для этого надо
взять x2=x1+h. Если f1<f2, то надо поменять направление движения
(h=- h и взять x2=x1+h).
2) xk+1=xk+2* hk-1 пока не будет xm-1: fm-1< fm.
3) xm+1=(xm+xm-1)/2.
4) Из f(xm+1)и f(xm-1) взять минимальную
5) Переименовать а= xm-2 b= xm-1 с= xm+1 или а= xm-1 b= xm+1 с= xm
Шаг 2:
Найти d=b+1/2*((b-a)*(f(a)-f(c))/(f(a)-2*f(b)+f(c)));
Шаг 3:
КОП: Если l(d-b)/bl<=e1 и l(f(d)-f(b))/f(b)l<=e2 выполняются, то x*=(b-d)/2
Иначе: x0 = min(f(b),f(d)) и h1=h/2 goto Шаг1.
Метод Циклического покоординатного спуска:
В данном методе на каждой итерации выполняется n(количество координат) одномерных минимизаций (спусков) вдоль единичных орт. Этот метод работает особенно хорошо, если линии равного уровня расположены вдоль координатный осей.
Начальный этап
Выбрать x1, e, k=1, l=1.
Основной этап
Шаг 1
(1) В качестве направления p выбрать  , где ненулевая позиция имеет индекс l.
, где ненулевая позиция имеет индекс l.
(2) Найти L как результат минимизации функции по направлению p.
(3) 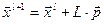
(4) Если l<n то Шаг 2, иначе повторить Шаг 1 с l = l+1.
Шаг 2
(1) Вычислить 
(2) Проверить КОП: если 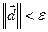 , то
, то  , иначе
, иначе  , l=1 и на Шаг 1.
, l=1 и на Шаг 1.
Текст программы:
#include <conio.h>
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <iostream.h>
double x01,x02,x1,x2,p1,p2,alfam=0.2, E=0.00001,a,b,g1,g2;
Void point(double alfa)
{
x1=x01+alfa*p1;
x2=x02+alfa*p2;
}
Double f(double x1,double x2)
{
return ((x2-x1*x1)*(x2-x1*x1)+100*(1-x1*x1)*(1-x1*x1));
}
Double df(double alfa)
{ point(alfa);
g1=4*(x1-2)*(x1-2)*(x1-2)+2*(x1-2*x2);
g2=-4*(x1-2*x2);
return (g1*p1+g1*p2);
}
Double f1(double alfa)
{ point(alfa);
return f(x1,x2);
}
void Swann(double* a,double* b)
{
double h1,x1;
h1=0.1;
x1=h1;
if(f1(0)<f1(x1))
{h1=-h1;
x1=h1; }
do {
h1=2*h1;
x1=x1+h1;
}
while(f1(x1-h1)>f1(x1));
*a=x1-1.5*h1;
*b=x1;
}
Double bolc(double a, double b)
{
double xk;
xk=(a+b)/2;
xk=(a+b)/2;
if (df(xk)>0)
{
b=xk;
}
Else
{
a=xk;
}
return xk;
}
Double DSK(double xk)
{
double x2, a, b, c, d, h, Min;
h = 0.01*xk;
if (!h)
h = 0.1;
x2 = xk + h;
if (f1(xk) < f1(x2))
h = -h;
do
{
x2 = xk + h;
while(f1(xk) > f1(x2))
{
h = 2*h;
xk = x2;
x2 = xk + h;
}
if (f1(xk) < f1((xk+x2)/2))
{
b = xk;
c = (xk+x2)/2;
a = 2*b - c;
}
Else
{
a = xk;
b = (xk+x2)/2;
c = 2*b - a;
}
d = b + (b-a)*(f1(a)-f1(c))/(f1(a) - 2*f1(b) + f1(c))/2;
h = h/2;
if (f1(b) < f1(d))
xk = b;
Else
xk = d;
}
while((fabs((d - b)/b) > E) || (fabs((f1(d) - f1(b))/f1(b)) > E));
Min = (b+d)/2;
return Min;
}
Double CPS(void)
{
int k=1;
p1=1;
p2=0;
if(f1(0)<f1(x1))
{ p1=-p1;
p2=-p2;
}
Swann(&a,&b);
alfam=bolc(a,b);
alfam=DSK(alfam);
k++;
p1=0;
p2=1;
if(f1(0)<f1(x1))
{ p1=-p1;
p2=-p2;
}
Swann(&a,&b);
alfam=bolc(a,b);
alfam=DSK(alfam);
k++;
cout<<"\nЧисло итераций k = "<<k<<"\n";
return alfam;
}
Void main()
{
clrscr();
cout<<" Введите координаты точки начала поиска x1 x2: "<<"\n";
cin>>x01>>x02;
alfam=CPS();
point(alfam);
cout<<"\ Точка минимума ("<<x1<<";"<<x2<<")"<<"\n";
getch();
}
Результаты тестирования метода:
Ниже приведена таблица с результатами работы программы для функции f(x) = 100(x2 - x12)2 + (1 - x1)2, с различными стартовыми точками и точностями вычисления.
| Точность: | 0.0001 | 0.00001 | 0.000001 | |||
| Метод ЦПС | К | x* | K | x* | K | x* |
| X0=(1;2) | (1, 1) | (1, 1) | (1, 1) |
Выводы:
В данной работе была разработана программа многомерной минимизации целевых функций на основе применения простых градиентных методов поиска. В данной программе использовался метод циклического покоординатного спуска.
Ответы на контрольные вопросы:
Поясните организацию линейного поиска на основе методов золотого сечения, Фибоначчи и Пауэлла.
Организация поиска минимума функции многих переменных в заданном направлении аналогична поиску минимума целевых функции. Различие заключается в описании (задании) функции, а также в методе Свенна, при помощи которого производится нахождение интервала локализации минимума.
Рассмотрим метод Свенна для функции многих переменных.
Его отличие заключается в том, что для опредения направления убывания функции мы определяем значение производной функции в нуле. Если оно больше нуля тогда знак шага фукции a меняется на противопложный. А удвоение шага происходит до тех пор пока не поменяет знак значения произведения производных функции на концах отрезка.
В своей работе я задавал функцию описывая каждую переменную через шаг функции - a.
Методы золотого сечения и метод Пауэлла приведены в данном отчёте в пункте описания методов оптимизации.
2. Найти производную dfx в точке x1=(1,0)t по направлению p1=(1,1)t для функции
f(x) = x12 – x1x2 + 2*(x2)2 - 2x1.
g1=2x1-x1-2=2-2=0.
g2=-x1+4*(x2)= -1
Таким образом dfx = g1*p1 + g2*p2 = 0*1 + (-1)*1 = -1.
3. Как изменится процедура минимизации методами Больцано, дихотомии, ДСК, Дэвидона при переходе от поиска на числовой прямой к поиску на плоскости R2?
При минимизации вышеуказанными методами на числовой прямой направление всегда фиксировано и задается во всех используемых методах изначально. При поиске на плоскости  применяются градиентные методы, в которых направленеи изменяется, т.е. необходимо подавать не постонные значения направления, а переменные.
применяются градиентные методы, в которых направленеи изменяется, т.е. необходимо подавать не постонные значения направления, а переменные.
4. Что является направлением наискорейшего спуска в точке x = (1,1)t для целевой функции y(x) = x12 + 2x22 ?
Направлени наискорейшего спуска.
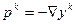 (вычислим антиградиентное направление движения)
(вычислим антиградиентное направление движения)

5. Найдите минимум y(x) = x12 - x1x2 + 2x22 - 2x1 + ex1+x2, двигаясь из точки x = (0,0) в направлении наискорейшего спуска.
- (0.4998;-0.4998)