ЛАБОРАТОРНАЯ РАБОТА № 6. ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ АКТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО СОПРОТИВЛЕНИЙ. РЕЗОНАНС ТОКОВ
Цель работы: Экспериментальное исследование различных режимов работы разветвленной электрической цепи, состоящей из двух параллельных ветвей. В первую ветвь включена катушка индуктивности с постоянными параметрами L, r, а во вторую ветвь - конденсатор переменной емкости С. Исследование режима резонанса токов.
Общие теоретические сведения
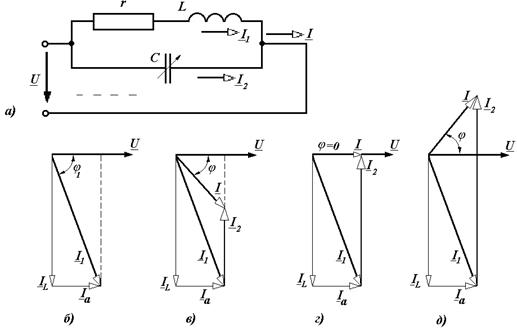
В схеме (рис. 6.1,а) общий ток  , согласно первому закону Кирхгофа, равен геометрической сумме токов или сумме комплексных токов в параллельных ветвях:
, согласно первому закону Кирхгофа, равен геометрической сумме токов или сумме комплексных токов в параллельных ветвях:
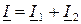 (6.1)
(6.1)
Векторные диаграммы этой схемы при различных значениях емкости С представлена на рис. 6.1,б, в, г, д. Сопротивление r и индуктивность L во время опыта не изменяются, следовательно и ток 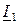 будет неизменным по своей величине и отставать от напряжения
будет неизменным по своей величине и отставать от напряжения  на угол j 1=
на угол j 1= 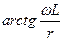 =const. Ток
=const. Ток 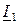 может быть разложен на две составляющие: активную
может быть разложен на две составляющие: активную 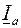 и реактивную
и реактивную 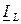 . Составляющая
. Составляющая 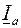 совпадает по направлению с напряжением
совпадает по направлению с напряжением  , а
, а 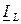 - отстает от напряжения
- отстает от напряжения  на 900. Эти составляющие связаны с напряжением
на 900. Эти составляющие связаны с напряжением  соотношениями:
соотношениями:
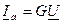 (6.2)
(6.2)
и 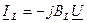 , (6.3)
, (6.3)
где 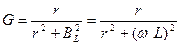 (6.4)
(6.4)
и 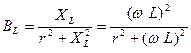 - (6.5)
- (6.5)
активная и реактивная проводимости.
Ток в ветви с конденсатором 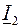 чисто реактивный и опережает напряжение
чисто реактивный и опережает напряжение  на 900, т. е. имеет направление, противоположное реактивной составляющей
на 900, т. е. имеет направление, противоположное реактивной составляющей 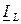 :
:
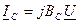 , (6.6)
, (6.6)
где 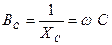 - (6.7)
- (6.7)
емкостная проводимость.
Величина общего тока определится:
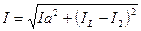 (6.8)
(6.8)
а угол сдвига между напряжением  и общим током
и общим током 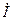 определяется из соотношения
определяется из соотношения
cos j = I a / I (6.9)
|
Рис.6.1. Принципиальная схема (а) и ее векторные диаграммы (б, в, г, д) при различных значениях емкости конденсатора С.
Если емкость C конденсатора подобрать так, чтобы ток 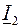 полностью компенсировал реактивную составляющую
полностью компенсировал реактивную составляющую 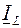 , то общий ток будет совпадать по направлению с напряжением
, то общий ток будет совпадать по направлению с напряжением  (рис. 6.1,г). Это явление называется резонансом токов. Условие резонансов токов:
(рис. 6.1,г). Это явление называется резонансом токов. Условие резонансов токов:
I L = I 2 или UBL= UBC, или BL = BC. (6.10)
При резонансе токов cos j = 1, 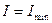 . Из сети потребляется только активная мощность. Индуктивность и емкость обмениваются реактивной мощностью. Равные по величине и противоположные по знаку токи
. Из сети потребляется только активная мощность. Индуктивность и емкость обмениваются реактивной мощностью. Равные по величине и противоположные по знаку токи 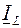 и
и 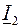 представляют по существу один реактивный ток, замыкающийся в контуре. Явление резонанса используется в энергетике для улучшения коэффициента мощности электрических установок. При cos j = 1 источники электрической энергии (генераторы, трансформаторы) используются наиболее эффективно, т. к. развивают наибольшую активную мощность
представляют по существу один реактивный ток, замыкающийся в контуре. Явление резонанса используется в энергетике для улучшения коэффициента мощности электрических установок. При cos j = 1 источники электрической энергии (генераторы, трансформаторы) используются наиболее эффективно, т. к. развивают наибольшую активную мощность
P = U ном I ном cos j = U ном I ном (6.7)
Порядок выполнения работы
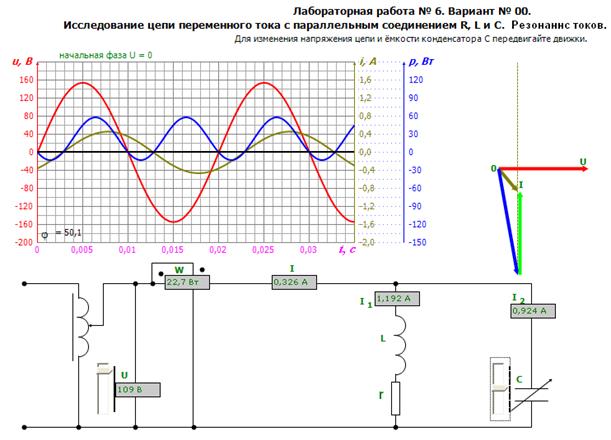
1. Электрическая принципиальная схема проведения опыта показана на рис.6.2. Параметры катушки индуктивности L, r и величина входного напряжения, задаются компьютером по варианту и во время опыта не изменяются.
2. Исследовать схему при изменении емкости конденсатора С от нуля до максимального значения, выполнив 9 замеров: 4 замера до резонанса, резонанс и 4 замера после резонанса.. Результаты измерений свести в таблицу 6.1.
|
,
Рис.6.2. Вид активного окна лабораторной работы №6. Схема для исследования резонанса токов.
Формулы для расчетов: сos j = P / UI; Z = U / I; cos j 1 = P / UI 1;
 ; Y1 = I 1/ U;
; Y1 = I 1/ U;  ; B С = 1/ X С = I 2/ U;
; B С = 1/ X С = I 2/ U;
Q L = B L U 2 ; Q C = B C U 2 ; Q = Q L - Q C .
3. Результаты расчетов занести сначала для проверки в таблицу 6.2 в компьютере (вызвав ее из меню), а затем в такую же таблицу в отчете;
Таблица 6.2
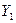
| 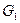
| 
| 
| cosφ1 |
| Cм | См | См | вар | _ |
3. Начертить в одном масштабе векторные диаграммы для случаев: BL > BC ; BL = BC; BL < BC. Величины активной и реактивной составляющей тока 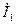 , определяются по формулам: I a = G 1 U; I L = B L U.
, определяются по формулам: I a = G 1 U; I L = B L U.
4. По результатам измерений (таблица 6.1) начертить зависимости: I; I 1; I 2; P; Q; cos j; Z = f (C) и объяснить их.
5. Дать заключение по результатам проделанной работы.
Контрольные вопросы
1. При каких условиях наступает резонанс токов?
2. Пояснить физическую сущность изменения проводимостей BL ; BC; Y при изменении частоты приложенного напряжения.
3. Почему стремятся повысить коэффициент мощности электрических установок?
4. Почему реактивная мощность всей цепи при резонансе токов равна нулю?
|
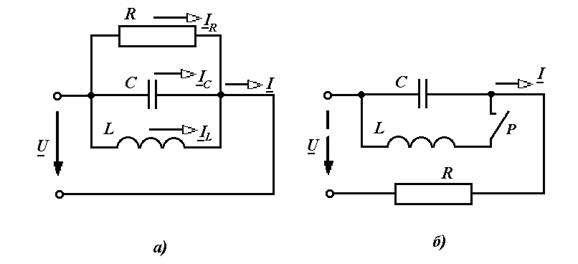
Рис.6.3. Разветвленные схемы с элементами RLC.
5. При напряжении U = 100 B и f = 50 Гц (рис. 6.3,а) Р = 100 Вт; Q L = 200 вар; Q C = 400 вар. Определить мощности при напряжении U = 200 В и f = 100 Гц.
7. Какое из выражений непригодно для определения общего тока I (рис. 6.3,а)
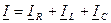 ;
;  ;
;
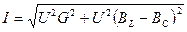 ;
;  .
.
8. Начертить векторные диаграммы (рис. 6.3,а) для случаев:
BL > BC; BL = BC; BL < BC .
9. Как изменяются токи I и IС (рис. 6.3,б) после включения рубильника, если X L = X C?
Таблица 6.1
| № пп | Измерено | Вычислено | |||||||||||||
| U | I | I1 | I2 | Р | сosj | Z | сosj1 | Y 1 | G1 | BL | BC | QL | QC | Q | |
| В | А | А | А | Вт | - | Ом | - | Cм | Вар | ||||||
| 0,529 | 1,094 | 1,57 | 0,3592 | 189,0359 | 0,1737 | 0,0109 | 0,0019 | 0,0107 | 0,0157 | -50 | |||||
| 0,36 | 1,382 | 19,1 | 0,5306 | 277,7777 | 0,1746 | 0,00191 | 0,0107 | 0,0138 | -31 | ||||||
| 0,224 | 1,193 | 19,1 | 0,8527 | 446,4286 | 0,1746 | 0,00191 | 0,0107 | 0,0193 | -86 | ||||||
| 0,199 | 1,13 | 19,1 | 0,9598 | 502,5126 | 0,1746 | 0,00191 | 0,0107 | 0,0113 | -6 | ||||||
| 0,192 | 1,068 | 19,1 | 0,9947 | 520,8333 | 0,1746 | 0,00191 | 0,0107 | 0,0107 | |||||||
| 0,205 | 1,005 | 19,1 | 0,9317 | 487,8049 | 0,1746 | 0,00191 | 0,0107 | 0,01005 | |||||||
| 0,234 | 0,942 | 19,1 | 0,8162 | 427,3504 | 0,1746 | 0,00191 | 0,0107 | 0,0094 | |||||||
| 0,299 | 0,848 | 19,1 | 0,6388 | 334,4482 | 0,1746 | 0,00191 | 0,0107 | 0,0085 | |||||||
| 0,576 | 0,534 | 0,3316 | 173,6111 | 0,1737 | 0,0019 | 0,0107 | 0,0053 |