Граф в математике определяется как конечная совокупность точек, называемая вершинами; некоторые из них соединены друг с другом линиями, называемыми ребрами графа (см. рисунок 9.4.).
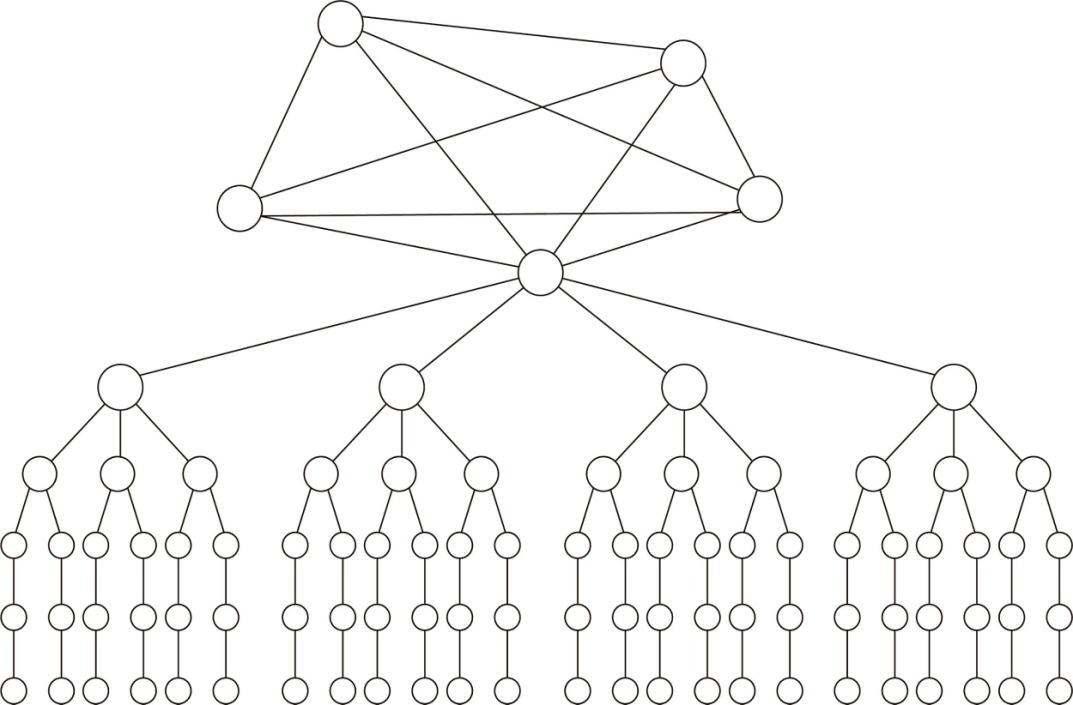
Рисунок 9.4.
При взгляде на географическую карту сразу бросается в глаза сеть железных дорог. Это типичный граф: круги обозначают станции – вершины графа, а соединяющие их пути – ребра.
Пример 1.
В строительстве графы используются при планировании проведения работ. Граф, изображенный на рисунке 9.5., называется сетевым графиком строительства. В данном случае он составлен для строительства жилого дома.

Рисунок 9.5.
Вершины этого графа обозначают отдельные виды работ на стройке, кроме того, есть еще две вершины: начало строительства и его окончание. Если на ребрах графа нанесены стрелки, указывающие направление ребер, то такой граф называют направленным или ориентированным.
Стрелка от работы (А) к работе (В) на графе означает, что работа (В) не может начаться раньше, чем кончится работа (А). Нельзя начинать монтаж стен, не закончив строить фундамент; чтобы приступить к отделке, нужно иметь на этажах воду; для сварочных работ при монтаже нужно иметь подвод электричества и т. д.
Около вершин графа указаны числа – продолжительность в днях соответствующей работы. Теперь мы можем узнать наименьшую возможную продолжительность строительства. Для этого из всех путей по графу в направлении стрелок нужно выбрать путь, у которого сумма чисел при вершинах наибольшая. Он называется критическим путем (выделен коричневым цветом). В нашем случае получаем 170 дней. Ну а если сократить время прокладки электросети с 40 до 10 дней, то и время строительства тоже сократится на 30 дней? Нет. В этом случае критический путь станет проходить не через эту вершину, а через вершины, соответствующие строительству котлована, укладке фундамента и т. д. И общее время строительства составит 160 дней, т. е. срок сократится лишь на 10 дней.
Материал взят из Энциклопедического словаря юного математика для среднего и старшего школьного возраста. Составитель А. П. Савин.
Пример 2.

Рисунок 9.6.
Имеется ориентированный граф (см. рисунок 9.6.). На основе графа строится матрица, которая отображает расстояния между доступными вершинами графа. Такая матрица называется матрицей смежности.
По стрелкам направлений видно, что мы можем попасть из 4 вершины в 5, а также из 5 обратно в 4. Однако из 2 вершины попасть в 5 можно, а обратно нельзя.
Так заполняются поля матрицы. Если прохода нет – пишется 0.
Матрица смежности:
Одно из математических решений таких задач – алгоритм Шимбелла, основанный на сложении матриц. Чтобы узнать кратчайший путь от одной вершины к другой из двух ребер, мы складываем поочередно каждый элемент соответствующей номерам вершин строки и столбца. Причем операции, где фигурирует хотя бы один ноль, мы игнорируем. А из получившихся при сложении пар элементов кратчайших цифр выбираем наименьшую.
Итак, путь от элемента 3 к элементу 2:
0+10 (0)
0+ 0 (0)
0 +0 (0)
8+6 (14)
0+0 (0)
Единственная операция, которая удовлетворяет нашим условиям, дает 14. Теперь посмотрим на рисунок в самом верху – единственный кратчайший путь из двух ребер от вершины 3 к вершине 2 будет проходить через 4-ю и иметь вес 14.
Матрица для кратчайших путей из двух ребер:
В первом приближении нам нужно в двойном цикле пройти все элементы двумерного массива. Нужен и третий цикл внутри двух первых, который будет на каждом шаге складывать элемент искомых строки и столбца.
При этом нужно создать простейший набор условий, который поможет нам отбросить операции, где фигурирует хоть один ноль, и операции с одинаковыми номерами строки и столбца (пример: элемент с адресом 3.4 просчитать можно, а вот 3.3 – это вершина 3. А из вершины 3 мы не можем пройти в вершину 3, мы уже там находимся).
При вычислении матрицы для путей из трех ребер необходимо будет складывать элементы строки и столбца первой и второй полученных матриц. В самом алгоритме изменятся только слагаемые. Переписывать его уже не потребуется.
Условия задания:

Рисунок 9.7.
Департамент Федеральной службы по экологическому, технологическому и атомному надзору по Северо-Западному округу сообщил об обнаруженных нарушениях и несоблюдении требований по охране водных объектов: сброс нефтесодержащих сточных вод.
По данным департамента был зафиксирован сброс нефтепродуктов в акваторию Н (см. рисунок 9.7.). В ходе обследования территории были выявлены 4 нефтяные вышки (А), (Б), (В), (Г), осуществляющие сброс нефтепродуктов в воду.
Вам необходимо покинуть департамент Гидрометслужбы (М), выполнить необходимые сборы проб воды и отправить их обратно в Гидрометслужбу (М) для проведения экспертизы.
Провести отбор может только беспилотное судно с небольшой осадкой. Выполнять заборы воды предстоит в пасмурную погоду, так что на зарядку от солнечных батарей не стоит рассчитывать. Заряда аккумулятора хватит на прохождение всех точек по кратчайшему маршруту, иначе дрон останется без управления.
Департамент сообщил координаты в системе GPS. Подготовьтесь к операции – вычислите расстояние, создайте алгоритм и напишите программу для определения кратчайшего маршрута.
Пример задания координат:
| Точка | Широта сев. | Долгота вост. |
| А | 61.054980 | 31.196363 |
| Б | 61.132958 | 31.092423 |
| В | 61.107183 | 30.937945 |
| Г | 61.018907 | 31.112561 |
| М | 60.878341 | 31.372899 |
Задачи:
Разработать и реализовать на языке C/C++ алгоритм, на его основе создать программу. Программа должна:
● вычислять расстояние между объектами, учитывая, что Земля имеет форму сферы;
● определять кратчайший маршрут, проходящий через указанные координаты по одному разу с последующим возвратом в исходную точку.
Разработка алгоритма
На вход алгоритма подаются заданные GPS координаты. Первая точка заданных координат является местом старта и финиша дрона. Алгоритм должен выдать наиболее выгодную последовательность посещения указанных точек. Началом и концом последовательности всегда будет являться первая точка из заданных GPS координат.
Если задача решена не с помощью полного перебора вариантов, то необходимо указать, какой алгоритм использовался, и дать подробное описание работы. При решении задачи точки координат следует представлять как вершины графа, а все возможные пути как его ребра.
Решением данной задачи является гамильтонов цикл, то есть такой путь, который проходит через каждую вершину графа ровно по одному разу.
Вариант выполнения 1
Для реализации алгоритма на 5 точках предлагается воспользоваться структурой. Название структуры и полей структуры должно полностью соответствовать заданной ниже.
| struct st { int points = 5;//количество точек int speed = 8;//средняя скорость дрона в км в ч int time = 0;//время в пути в часах double gps [5][2] = {0.0};// координаты gps широта сев., долгота вост. double distance[5][5] = {0.0};// матрица смежности графа расстояний int route [6] = {0};// последовательность посещений точек // то есть изначальному положению дрона. double routeLength = 0.0; st(double g [5][2])// конструктор структуры { for(int i = 0; i < 5; i++) { gps[i][0] = g[i][0]; gps[i][1] = g[i][1]; } } }; |
В ходе выполнения задания необходимо реализовать следующие функции:
| void showMap (st task);//вывод значений точек gps; void showDistance (st task);//вывод матрицы смежности; void showRoute (st task);// вывод последовательности посещения; st makeDistance (st task);//расчет дистанций, матрицы смежности; st makeRoute (st task);//поиск оптимального маршрута. |
Сигнатура функция должна полностью соответствовать примеру.
Также требуется вывести на экран время в часах, необходимое для преодоления пути.
| Входные данные | Вывод на экран | Значения ключевых переменных после выполнения программы |
| double g [5][2] = {{59.458953, 30.316287}, {59.515355, 30.368472}, {59.518670, 30.474215}, {59.437800, 30.488635}, {59.426781, 30.423747}}; | distance: 0 6.92917 11.1168 10.0214 7.04991 6.92917 0 5.97605 10.9736 10.332 11.1168 5.97605 0 9.02913 10.6078 10.0214 10.9736 9.02913 0 3.86851 7.04991 10.332 10.6078 3.86851 0 time: 4.1066 hours route 0 4 3 2 1 0 | routeTest [6] = {0, 4, 3, 2, 1, 0} |
Критерии оценки
Проверяться будут только ключевые переменные. Проверка будет производиться последовательным вызовом функций st makeDistance (st task) и st makeRoute (st task). После выполнения алгоритма последняя функция должна вернуть структуру с корректно заполненным массивом int route [ 6 ]. Если после выполнения программы вывод на экран верен, а значение в массиве routeTest неверно, то балл за задание не начисляется.
Пример выполненного задания:
1 int main ()
2 {
3 double g [ 5 ][ 2 ] = {{ 59.458953, 30.316287 },
4 { 59.515355, 30.368472 },
5 { 59.518670, 30.474215 },
6 { 59.437800, 30.488635 },
7 { 59.426781, 30.423747 }};
8 st task(g);//создание объекта task типа st
9 task = makeDistance(task);
10 showDistance(task);
11 task = makeRoute(task);
12 return 0;
13 }
В качестве правильного ответа будет приниматься как прямой порядок прохождения маршрута, так и обратный, так как они идентичны по длине. Гарантируется, что точки подобраны таким образом, что неточность до 10 метров не будет влиять на результат маршрута. Пример работы тестирующей программы приведен ниже в таблице. Всего будет проводиться 20 тестов. За каждый пройденный тест участник получает 1 балл. Также будет учитываться время работы функций makeDistance и makeRoute.
| Test 1 done Right answer: 0 4 3 2 1 0 Your answer: 0 4 3 2 1 0 | Test 1 done Right answer: 0 4 3 2 1 0 Your answer: 0 1 2 3 4 0 | Test 1 failed! Your answer: 0 2 1 3 4 0 Right answer: 0 4 3 2 1 0 |
Вариант выполнения 2
За дополнительные баллы предлагается реализовать такой же алгоритм с использованием возможностей C++. Алгоритм реализуется с использованием шаблона vector, что ускоряет его работу и при знании особенностей работы с ООП и шаблонами значительно упрощает написание кода программы. Ниже приведен класс, методы которого необходимо реализовать.
| class Points{ public: std::vector<std::vector<double>> GPS; std::vector<std::vector<double>> distance; std::vector<int> road; int speed = 8;//средняя скорость дрона в км в ч int time = 0;//время в пути в часах Points(); Points(std::vector<std::vector<double>> point); void showGps (); void showDistance (); void makeDistance (); void makeRoad (); void showRoad(); }; |
В данном случае алгоритм будет работать быстрее, так как не требуется при вызове каждого метода копировать все данные класса, что происходило при работе со структурами. Пример программы с реализацией возможностей C++:
| int main() { std::vector<std::vector<double>> gps = {{59.458953, 30.316287}, {59.515355, 30.368472}, {59.518670, 30.474215}, {59.437800, 30.488635}, {59.426781, 30.423747}}; Points test(gps); test.makeDistance(); test.makeRoad(); } |
Критерии оценки
После выполнения программы в поле std::vector< int > road; объекта test должна находиться корректная последовательность точек. Для данного примера она соответствует предыдущему заданию со структурой. Как видно из конструктора класс, нигде не сообщается количество GPS координат. Длину вектора GPS можно получить методом GPS.size(). В данном примере его длина будет равна 5, что соответствует количеству точек. Тестирование будет проводиться на разном количестве точек от 5 до 50 и будет также содержать 20 тестов, но при решении задачи данным методом за каждый пройденный тест участник будет получать не 1, а 2 балла. Задача нахождения оптимального маршрута через все точки относиться к классу трансвычислительных и уже при относительно небольшом числе точек (66 и более) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет. Это означает, что для прохождения теста с 50 точками метод полного перебора категорически запрещен.
Гарантируется, что точки для тестирования будут одинаковы для всех участников, как для варианта 1, так и для варианта 2.
Для ознакомления со структурой графов и базовыми алгоритмами рекомендуется книга: Хайнеман, Поллис, Селков: Алгоритмы. Справочник с примерами на C, C++, Java и Python.
Команда, программа которой выполняет задание за наименьшее среднее время по всем тестам, получит дополнительно 5 баллов.
Приложение 3