Практикум на ЭВМ. Алгоритмы

П 691 Учебное пособие / В.П. Хиценко, Т.А. Шапошникова. – Новосибирск: Изд-во НГТУ, 2004. – 112 с.

 

Рассмотрены основные алгоритмы, изучаемые в курсе «Практикум на ЭВМ»: алгоритмы на графах, комбинаторные алгоритмы, алгоритмы полного перебора. Разобрано много примеров, иллюстрирующих теоретический материал.

 

 

УДК 004.421+519.1](075.8)

 

 

 

© Новосибирский государственный
технический университет, 2004

 

оглавление

Курс «Практикум на ЭВМ» является первой базовой дисциплиной среди программистских дисциплин. Нельзя овладеть программированием без знания важнейших и известнейших алгоритмов. В данном учебном пособии подробно разобраны алгоритмы, широко применяемые при решении разных классов задач: основные алгоритмы на графах, алгоритм полного перебора и методы его улучшения (алгоритмы динамического программирования, «жадный» алгоритм, метод ветвей и границ), алгоритмы формирования основных комбинаторных объектов.

Учебное пособие предназначено не только для студентов, изучающих начальные разделы программирования, но и для тех, кто желает обогатить свои навыки конструирования алгоритмов (вместо «изобретения очередного велосипеда»). Часто разница между плохим и хорошим алгоритмами более существенна, чем между быстрым и медленным компьютерами. Например, мы хотим отсортировать массив из миллиона чисел. Что быстрее – отсортировать его вставками на супер–компьютере (100 миллионов операций в секунду) или слиянием на домашнем компьютере (1 миллион операций)? При этом, если сортировка вставками написана на ассемблере чрезвычайно экономно, для сортировки n чисел нужно приблизительно 2 n ² операций. В то же время алгоритм слиянием написан без особой заботы об эффективности и требует 50· n · log n операций. В первом случае для сортировки 1 миллиона чисел получаем:

для супер–компьютера:

для домашнего компьютера:

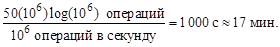
Отсюда видно, что разработка эффективных алгоритмов не менее важна, чем разработка быстрой электроники.

Учебное пособие дополняет лекционный и практический материал дисциплины «Практикум на ЭВМ» и ориентировано прежде всего на поддержку самостоятельной работы студентов при выполнении РГР и курсовых работ. Поэтому каждый алгоритм, приведенный в учебном пособии, разобран на практическом примере, для некоторых приведена программная реализация на языке программирования (Си). Также для алгоритмов даны оценки их сложности.

Алгоритмы записаны в виде «псевдокода», прокомментированы в тексте, наглядно представлены на рисунках и в таблицах.

 

 

 

1. Основные алгоритмы на графах

Математические модели большого числа задач могут быть описаны в терминах теории графов, поэтому алгоритмы исследования структуры (обработки) графов, а также способы их представления очень важны.

1.1. Некоторые основные определения

Графом (неориентированным графом) G(V,E) называется совокупность двух множеств, где V – конечное непустое множество элементов, называемых вершинами, а E – множество неупорядоченных пар различных элементов множества V (эти пары называются ребрами). Граф, состоящий из одной вершины, называется тривиальным.

Говорят, что ребро e = (u, v) соединяет вершины u и v. Ребро e и вершина u (а также e и v) называются инцидентными, а вершины u и v – смежными. Ребра, инцидентные одной и той же вершине, также называются смежными.

Степень вершины – это число ребер, инцидентных ей. Вершина графа, имеющая степень 0, называется изолированной, а имеющая степень 1, – висячей.

Если E является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф – мультиграфом.

Если элементом множества E может быть пара одинаковых (не различных) элементов V, то такой элемент E называется петлей. Псевдограф – это граф, у которого наряду с кратными ребрами допускаются и петли, причем даже несколько петель при одной вершине.

Граф называется простым, если любая пара вершин соединена не более чем одним ребром и граф не имеет петель.

Маршрут (путь) – это чередующаяся последовательность

a = v₀, e₁, v₁, e₂,..., v_n–1, e_n, v_n = b

вершин и ребер графа такая, что e_i = (v_{i- 1}, v_i),1 ≤ i ≤ n. Говорят, что маршрут соединяет вершины a и b – концы маршрута. В простом графе маршрут можно задать перечислением лишь его вершин a = v ₀, v ₁, …, v_n = b или его ребер e ₁, e ₂, …, e_n.

Маршрут называется цепью, если все его ребра различные. Маршрут называется замкнутым, если v ₀ = v_n.

Замкнутая цепь называется циклом. Цепь называется простой, если не содержит одинаковых вершин. Простая замкнутая цепь называется простым циклом.

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа.

Вершина u достижима из вершины v, если существует путь из v в u.

Длина пути v ₀, v ₁, …, v_n равна числу его ребер, т.е. n.

Расстояние между двумя вершинами – это длина кратчайшего пути, соединяющего эти вершины.

Часть графа G(V, E) – это такой граф G'(V',E'), что V' Í V и E' Í E.

Подграфом графа G называется такаяего часть G', которая вместе со всякой парой вершин u, v содержит и ребро (u, v), если оно есть в G.

Дополнением графа G называется граф G' с тем же множеством вершин, что и у G, причем две различные вершины смежны в G' тогда и только тогда, когда они несмежны в G. Ребра графов G и G' вместе образуют полный граф. Граф называется полным, если любые две его вершины смежны.

Два графа G 1 и G 2 изоморфны, если существует взаимно однозначное отображение множества вершин графа G 1 на множество вершин графа G 2, сохраняющее смежность.

Граф называется связным, если для любой пары вершин существует соединяющий их путь. Максимальный связный подграф несвязанного графа называется компонентой связности данного графа.

Если задана функция F: V → M, то множество M называется множеством пометок, а граф – помеченным. Если задана функция F: E → M, т.е. ребрам графа приписаны веса, то граф называется взвешенным.

Ребро графа называется ориентированным, если существен порядок расположения его концов. Граф, все ребра которого ориентированные, называется ориентированным графом (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества E – дугами. Дуга (u, v) ведет от вершины u к вершине v, Вершину v называют преемником вершины u, а u – предшественником вершины v. Понятия части орграфа, пути, расстояния, простого и замкнутого пути, цикла определяются для орграфа так же, как и для графа, но с учетом ориентации дуг.

Источник орграфа – это вершина, от которой достижимы все остальные вершины. Сток орграфа – это вершина, достижимая со всех других вершин.

Деревом называется связный граф без циклов.

Корневое дерево – это связный орграф без циклов, удовлетворяющий условиям:

1) имеется единственная вершина, называемая корнем, в которую не входит ни одна дуга;

2) к каждой некорневой вершине ведет одна дуга.

Вершины, из которых не выходит ни одна дуга, называются листьями.

1.2. Представление графов в ЭВМ

Представление в программе объектов математической модели – это важная составляющая программирования. Выбор наилучшего представления определяется требованиями конкретной задачи. Известны различные способы представления графов в памяти компьютера. Они различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Следует заметить, что во многих задачах на графах выбор представления – решающий для эффективности алгоритмов. На рис. 1.1 для неориентированного (а, б, в, г) и ориентированного (д, е, ж, з) графов показаны различные представления: б, е – матрица смежности; в, ж – матрица инцидентности; г – список смежности неориентированного графа при смежном размещении элементов списка; з – список смежности ориентированного графа при связанном размещении элементов списка.

1.2.1. Матрица смежности графа

Матрицей смежности помеченного графа с n вершинами называется матрица A = [ a_ij ], i, j = 1, 2,..., n, в которой

Матрица смежности однозначно определяет граф (рис. 1.1, а–в, д–е). Для неориентированного графа матрица A является симметричной относительно главной диагонали. Число единиц в строке равно степени соответствующей вершины. Петля в матрице смежности может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1.

Преимуществом такого представления является «прямой доступ» к ребрам графа, т.е. имеется возможность за один шаг получить ответ на вопрос «существует ли в графе ребро (x, y)?» Для небольших графов, когда места в памяти достаточно, с матрицей смежности часто проще работать. Недостаток заключается в том, что независимо от числа ребер объем занимаемой памяти составляет n ´ n или n ´ n /2 – n, если использовать симметрию и хранить только треугольную подматрицу матрицы смежности. Кроме того, каждый элемент матрицы достаточно представить одним двоичным разрядом.

1.2.2. Матрица инцидентности графа

Матрицей инцидентности называется матрица B = [ b_ij ], i = 1,2,..., n, j = 1, 2,..., m (где n – число вершин, а m – число ребер графа), строки которой соответствуют вершинам, а столбцы – ребрам. Элемент матрицы в неориентированном графе равен:

В случае ориентированного графа с n вершинами и m дугами элемент матрицы инцидентности равен:

Строки матрицы также соответствуют вершинам, а столбцы – дугам.

Матрица инцидентности однозначно определяет структуру графа (рис. 1.1, а – в, д–ж). В каждом столбце матрицы B ровно две единицы. Равных столбцов нет.

Недостаток данного представления состоит в том, что требуется n ´ m единиц памяти, большинство из которых будет занято нулями. Не всегда удобен доступ к информации. Например, для ответа на вопросы «есть ли в графе дуга (x, y)?» или «к каким вершинам ведут ребра из вершины x?» может потребоваться перебор всех столбцов матрицы.

1.2.3. Матрица весов графа

Простой взвешенный граф может быть представлен своей матрицей весов W = [ w_ij ], где w_ij – вес ребра, соединяющего вершины i, j = 1,2,..., m. Веса несуществующих ребер полагаются равными ∞ или 0 в зависимости от задачи. Матрица весов – простое обобщение матрицы смежности.

1.2.4. Список ребер графа

При описании графа списком его ребер (или для орграфов списком дуг) каждое ребро представляется парой инцидентных ему вершин. Это представление можно реализовать двумя массивами (или одним двумерным):

x = (x₀, x₁,..., x_m) и y = (y₀, y₁,..., y_m),

где m –– количество ребер в графе. Каждый элемент в массиве есть метка вершины, а i -еребро графа выходит из вершины x_i и входит в вершину y_i. Объем занимаемой памяти составляет в этом случае 2 m единиц памяти. Неудобством является большое число шагов, необходимое для получения множества вершин, к которым ведут ребра из данной вершины.

1.2.5. Списки смежных вершин графа

Граф может быть однозначно представлен структурой смежности своих вершин. Структура смежности состоит из списков Adj [ x ] вершин графа, смежных с вершиной x. Списки Adj [ x ] составляются для каждой вершины графа. Структура смежности удобно реализуется массивом из n (число вершин в графе)
линейно связанных списков (1.1, а–г). Каждый список содержит

 

а д

б е

½

1/3

1/5

2/3

3/4

3/5

4/5

½

1/3

4/1

4/2

5/4

-1

-1

-1

-1

-1

в ж

г з

Рис. 1.1

вершины, смежные с вершиной, для которой составляется список. Список смежных вершин графа дает компактное представление для разреженных графов – тех, у которых множество ребер много меньше множества вершин. Недостаток этого представления таков: если мы хотим узнать, есть ли в графе ребро (x, y), приходится просматривать весьсписок Adj [ x ] в поисках y. Объем требуемой памяти составляет для ориентированных n+ m и n+2m для неориентированных графов единиц памяти, где n – число вершин графа, а m – число ребер (дуг) графа. Если в основе алгоритма решения задачи лежат операции добавления и удаления вершин из списков, то хранение списков смежности удобно реализовать, используя связанное представление списков (1.1, д–з).

1.3. Обход графа

Обход графа – это некоторое систематическое прохождение его вершин (и/или ребер). Обходя граф, мы двигаемся по ребрам (дугам) и проходим все вершины. При этом можно получить много информации, которая необходима для дальнейшей обработки графа, поэтому обход графа – основа многих алгоритмов исследования структуры графа. Если при посещении вершины структура графа не меняется, то наиболее полезны два основные способа обхода: обход в глубину и обход в ширину.

1.3.1. Обход (или поиск) в глубину

Пусть задан граф и фиксирована начальная вершина s (исходный граф может быть неориентированным или ориентированным). Стратегия поиска в глубину состоит в том, чтобы, начиная с начальной вершины, идти «вглубь», пока это возможно (есть не пройденные исходящие ребра), и возвращаться и искать другой путь, когда таких ребер нет. Так делается, пока не обнаружены все вершины, достижимые из исходной. Если после этого остаются необнаруженные вершины, выбирается одна из них (как начальная) и процесс повторяется. Так делать до тех пор, пока мы не обнаружим все вершины графа.

Когда при поиске мы впервые обнаружим вершину v, смежную с вершиной u, необходимо отметить это событие. Алгоритм поиска в глубину использует для этого цвета (метки) вершин. Каждая из вершин вначале белая (не пройденная). Будучи обнаруженной, она становится серой. Когда вершина будет полностью обработана (т.е. когда список смежных с ней вершин будет просмотрен), она станет черной. Таким образом, в процессе поиска из графа выделяется часть – «дерево поиска в глубину» или несколько деревьев (лес поиска в глубину), если поиск повторяется из нескольких вершин. Каждая вершина попадает ровно в одно дерево поиска в глубину, так что эти деревья не пересекаются. Кроме этого можно ставить дополнительные метки на вершинах дерева: метку, когда вершина была обнаружена (сделалась серой), и метку, когда была закончена обработка списка смежных с u вершин (и u стала черной).

Приведенный ниже алгоритм использует представление графа списками смежных вершин Adj [ u ]. Для каждой вершины u графа дополнительно хранятся ее цвет Mark[ u ] и ее предшественник Pr[ u ]. Если предшественника нет (например, если u = s или u еще не обнаружена), то Pr[ u ] = nil. Кроме того, в d [ u ] и
f [ u ] записываются дополнительные для u метки: метки времени. В d [ u ] записывается время, когда вершина u была обнаружена (и стала серой), а в f [ u ] записывается время, когда была закончена обработка списка смежных с u вершин (и u стала черной). В приводимом ниже алгоритме метки времени d [ u ] и
f [ u ] это целые числа от 1 до 2×| V |; для любой вершины u выполнено неравенство: d [ u ] < f [ u ]. Вершина u будет белой до момента d [ u ], серой между d [ u ] и f [ u ] и черной после f [ u ]. Алгоритм использует рекурсию для просмотра всех смежных с
u вершин.

 

Поиск_в_глубину (G)

1 {

2 for (каждая вершина uÎ V [ G ])

3 { Mark [ u ]←БЕЛЫЙ;

4 Pr [ u ] ← nil;

5 }

6 time ←0;

7 for (каждая вершина sÎ V [ G ])

8 if (Mark [ u ] = БЕЛЫЙ) Search (s);

9 }

Search (u)

1 {

2 Mark [ u ] ←СЕРЫЙ;

3 d [ u ] ←time←time+1;

4 for (каждая v Î Adj [ u ])

5 { if (Mark [ v ] = БЕЛЫЙ)

6 { Pr [ v ] ← u; Search (v); }

7 }

8 Mark [ u ] ←ЧЕРНЫЙ;

9 f [ u ] ← time←time+1;

10 }

 

Алгоритм начинается с того, что сначала (строки 2–5) все вершины красятся в белый цвет (помечаются как не пройденные); в поле Pr помещается nil (пока у вершин нет предшественника). Затем (строка 6) устанавливается начальное (нулевое) время (переменная time – глобальная переменная). Для всех вершин (строки 7–8), которые все еще остались не пройденными (белыми), вызывается процедура Search. Эти вершины становятся корнями деревьев поиска в глубину.

В момент вызова Search (u) вершина u – белая. В процедуре Search она сразу же становится серой (строка 2). Время ее обнаружения (строка 3) заносится в d[ u ] (счетчик времени перед этим увеличился на единицу). Затем просматриваются (строки 4–7) смежные с u вершины; процедура Search вызывается для тех из них, которые оказываются белыми к моменту вызова. После просмотра всех смежных с u вершин саму вершину u делаем черной и записываем в f [ u ] время этого события.

Сложность поиска в глубину. Поскольку для каждой вершины, которую проходим впервые, выполняется обращение к процедуре один раз, то всего обращений будет │ V │. При каждом обращении количество производимых действий пропорционально числу ребер, инцидентных рассматриваемой вершине. Поэтому сложность поиска составляет O(V + E).

На рис. 1.2 для ориентированного графа (а) последовательно показано исполнение алгоритма Поиск_в_глубину. Белым цветом показаны еще не обнаруженные вершины, серым – обнаруженные, черным – обработанные вершины. После просмотра каждое ребро либо выделяется серым цветом (если оно включается в дерево поиска в глубину), либо не выделяется (при этом обратные ребра помечены буквой B, перекрестные – буквой C, прямые – буквой F). Для каждой вершины показаны времена начала d [ i ] (числитель дроби) и конца f [ i ] (знаменатель дроби) обработки.

 

Рис. 1.2

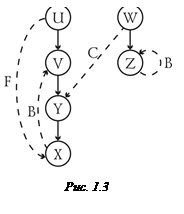Деревья поиска в глубину (дерево с корнем u и дерево с корнем w) для графа на рис. 1.2, а приведены на рис. 1.3. Сплошными стрелками показаны ребра деревьев, штриховыми – прямые (F), обратные (B) и перекрестные (C).

Свойства поиска в глубину. При поиске в глубину для любых двух вершин u и v выполняется одно из трех утверждений:

• отрезки [ d [ u ], f [ u ] ] и [ d [ v ], f [ v ] ] не пересекаются;

• отрезок [ d [ u ], f [ u ] ] целиком содержится внутри отрезка [ d [ v ], f[ v ] ] и u – потомок v в дереве поиска в глубину;

• отрезок [ d [ v ], f [ v ] ] целиком содержится внутри отрезка
[ d [ u ], f [ u ] ] и v – потомок u в дереве поиска в глубину.

Классификация ребер. Ребра графа можно разделить на несколько категорий в зависимости от их роли при поиске в глубину. Эта классификация бывает полезной в различных задачах.

1. Ребра деревьев (древесные ребра). Ребро (u, v) будет ребром дерева поиска в глубину, если вершина v была обнаружена при обработке этого ребра.

2. Обратные ребра – это ребра (u, v), соединяющие вершину u с ее предком v в дереве поиска в глубину. (Ребра-циклы, возможные в ориентированных графах, считаются обратными ребрами.)

3. Прямые ребра – это ребра, соединяющие вершину с ее потомком, но не входящие в дерево поиска в глубину.

4. Перекрестные ребра – все остальные ребра графа. Они могут соединять две вершины одного дерева поиска в глубину, если ни одна из этих вершин не является предком другой, или же вершины из разных деревьев.

В алгоритме Поиск_в_глубину можно различать тип ребер. Тип ребра (u, v) можно определить по цвету вершины v в тот момент, когда ребро первый раз исследуется: белый цвет означает ребро дерева, серый – обратное ребро, черный – прямое или перекрестное ребро. В неориентированном графе каждое ребро обрабатывается дважды: как ребро (u, v) и как ребро
(v, u). Если считать, что тип ребра определяется при его первой обработке и не меняется при второй, то оказывается, что в неориентированном графе прямых и перекрестных ребер нет.

1.3.2. Сильно связные компоненты и поиск в глубину

Классическое применение поиска в глубину – задача о разложении графа на сильно связные компоненты. Решение многих задач, использующих ориентированные графы, сводится к решению данной задачи отдельно для каждой компоненты связности, а общее решение комбинируется в соответствии со связями между компонентами.

Сильно связной компонентой ориентированного графа
G (V, E)называется максимальный по включению вершин подграф, множество вершин которого U Ì V. Любые две вершины
u и v из U достижимы друг из друга (т. е. есть путь из вершины u в вершину v и путь из v в u).

В процессе поиска в глубину вершины одной сильно связной компоненты попадают в одно и то же дерево поиска в глубину.

Алгоритм поиска сильно связных компонент ориентированного графа G = (V, E) будет использовать «транспонированный» граф G^T = (V,E^T), получаемый из исходного обращением стрелок на ребрах: E^T = {(u, v): (v, u)Î E }. Такой граф можно построить за время O (V + E), считая, что исходный и транспонированный графы заданы с помощью списков смежных вершин. Графы G и G^T имеют одни и те же сильно связные компоненты. Сильно связные компоненты ориентированного графа можно найти, выполняя дважды поиск в глубину: сначала для графа G (V, E), а затем для графа G^T (V, E^T).

 

STRONGL_Comp1 (G)

{

1 осуществить Поиск_в_глубину (G) и найти время окончания обработки для каждой вершины: f [ u ];

2 построить (G^T);

3 осуществить Поиск_в_глубину (G^T), при этом изменить внешний цикл в этом алгоритме, так чтобы перебирать вершины в порядке убывания величины f [ u ], вычисленной для графа G в шаге 1;

4 сильно связными компонентами будут деревья поиска, построенные в шаге 3;

}

На рис. 1.4, а показан ориентированный граф G и его сильно связные компоненты. У каждой вершины G показано время начала (числитель дроби) и конца (знаменатель дроби) обработки. Транспонированный граф G^T дан на рис.1.4, б. Каждая компонента и ребра деревьев поиска в глубину выделены серым цветом. Вершины B, C, G, H, выделенные черным цветом, являются корнями деревьев поиска в глубину для графа G^T.

 

Рис. 1.4

 

Для выделения компонент связности неориентированного графа достаточно пройти граф в глубину и расставить одинаковые метки у вершин, принадлежащих одной компоненте связности.

 

STRONGL_Comp2 (G)

1 {

2 for (каждая вершина uÎ V [ G ])

3 Mark [ u ]← 0;

4 count ← 0;

5 for (каждая вершина uÎ V [ G ])

6 if (Mark [ u ] = 0)

7 { count = count + 1;

8 Component (u, count); }

9 }

Component (u, count)

1 {

2 Mark [ u ] ←count;

3 for (каждая v Î Adj [ u ])

4 if (Mark [ v ] = 0)

5 Component (u, count);

6 }

 

Сначала все вершины помечаются как не пройденные (строки 2, 3). Переменная count – счетчик числа компонент получает начальное значение (строка 4). Значение этой переменной является одновременно и меткой вершин одной компоненты связности. Просматривая вершины, находим еще не обнаруженные вершины и увеличиваем число компонент связности (строки
5–7). Для всех вершин, которые остались еще не пройденными, вызывается процедура Component (строка 8).

В момент вызова Component (u) вершина u – не пройденная. В процедуре Component она сразу же становится пройденной и помечается меткой, равной номеру компоненты связности (строка 2). Затем просматриваются (строки 3–5) смежные с u вершины; процедура Component вызывается для тех из них, которые оказываются не пройденными к моменту вызова. При этом значение номера компоненты связности (значение count) не изменяется. Процесс заканчивается, когда будут просмотрены все вершины.

1.3.3. Примеры решения задач методом поиска в глубину

Рассмотрим использование метода поиска в глубину на двух простых примерах.

Задача 1. Для неориентированного графа G (V, E)требуется найти ребра дерева поиска в глубину (древесные и обратные).

Для решения этой задачи достаточно пройти граф в глубину и сохранить информацию о пройденных ребрах дерева поиска в глубину и об обратных ребрах, если такие есть. Если граф не связен, то будем находить ребра всех деревьев поиска. Алгоритм решения этой задачи полностью соответствует общей схеме прохода в глубину. В качестве «серых» меток обнаруженных вершин будем использовать целые числа в диапазоне от 0 до │ V │– 1, это позволит просто различать обратные ребра. Считаем, что вершины графа помечены целыми числами от 0 до │ V │– 1. Граф задан структурой смежности Adj [ u ]. Ребра дерева поиска (и обратные ребра) запоминаются в массиве T, а в массиве B запоминается признак ребра: 1 – ребро дерева, 0 – обратное ребро.

 

Программа нахождения ребер дерева поиска в глубину (язык Си)

# include <stdio.h>

# define maxn 100 //максимальное число вершин в графе

# define maxADj 1000 // максимальная длина списка смежности графа

int nT, count;

int Adj [maxADj]; //список смежности графа

int Fst [maxn]; //указатели на списки смежности для каждой v Î V

int Nbr [maxn]; //число вершин в списке смежности

для каждой v Î V

int Vt [maxn]; //список вершин графа

int Mark [maxn]; //метки вершин графа

int T [maxn]; //последовательность ребер при проходе

в глубину

int B [maxn]; //признаки основных и обратных ребер

//при проходе графа в глубину

// функция прохода графа в глубину и нахождения ребер дерева поиска

void Depth (int x, int s)

{

int i, v;

count ++;

Mark [x] = count // вершина x помечается как пройденная

// вершина

for (i = 0; i < Nbr[x]; i++) //просмотр списка смежности

// вершины x

{ v = Adj [Fst [x] + i]; //выбор из списка смежности x еще не

if (Mark [v] = = -1) //пройденной вершины

{ nT = nT +2; T [nT – 1] = x; T [nT] = v;

B [nT/2] = 1; //установлен признак основного ребра

Depth (v, x);

}

else

if (Mark [v] < Mark [x] && v!= s)

{ nT = nT +2; T [nT – 1] = x; T [nT] = v;

B [nT/2]=0; //установлен признак обратного ребра

}

}

}

// функция обнаружения не пройденных вершин графа

void WayDepth (void)

{

int u;

nT = -1; //глобальная переменная для вычисления индекса

//в массивах T и B

count = -1; //глобальная переменная для вычисления меток

//обнаруженных вершин

for (u = 0; u < n; u++) Mark[u] = -1; //сначала все вершины

// графа помечаем

// как не пройденные

for (u = 0; u < n; u++) //выбор очередной

if (Mark[u] = -1) Depth (u, -1); // не пройденной вершины

}

 

void main (void)

{

File *p, *f;

int i, j, n;

// ввод исходных данных

p = fopen(“spisok_Adj.in”, “r”);

if (fscanf (p, “%d”, &n)!= EOF)

{Fst [0] = 0; //установка указателя начала

//списка смежности для

//первой вершины

for (i = 0; i < n; i++)

{ fscanf (p, “%d”, &Vt [i]); //ввод метки вершины

fscanf (p, “%d”, &Nbr [i]); //ввод числа вершин

//в списке

// смежности вершины i

for (j = 0; j < Nbr [i]; j++) //ввод списка смежности

//вершины i

fscanf (p, “%d”, &Adj [ Fst [i] + j]);

Fst [i + 1] = Fst [i] + Nbr [i]; //установка указателя

//начала списка смежности

//следующей вершины

}

WayDepth (); // Проход графа в глубину

// вывод результатов

f = fopen(“spisok_reber.out”, “w”);

for (i = 0; i < nT/2; i++)

printf (f, “%d “, Vt [ T[2*i – 1] ]);

printf (f, “\n”);

for (i = 0; i < nT/2; i++)

printf (f, “%d “, Vt [ T[2*i ] ]);

printf (f, “\n”);

for (i = 0; i < nT/2; i++)

printf (f, “%d “, B [ i ]);

printf (f, “\n”);

fclose (p); fclose (f);

}

 

Рассмотрим работу программы на примере неориентированного графа, представленного на рис. 1.5. В графе семь вершин, помеченных целыми числами от 0 до 6.

 

 

Структура смежности этого графа:

 

v	Adj [ v ]
	1, 2, 4 0, 2, 3 0, 1, 3, 4 1, 2 0, 2, 5, 6 4, 6 4, 5

 

Исходные данные структуры смежности графа задаются в текстовом файле spisok_Adj.in в следующем формате:

• в первой строке файла содержится число вершин графа;

• далее для каждой вершины в отдельной строке указывается номер самой вершины, число вершин, смежных с данной, и список этих вершин (вершины перечисляются в порядке возрастания меток вершин).

 

Исходный файл для графа на рис. 1.5:

0 3 1 2 4

1 3 0 2 3

2 4 0 1 3 4

3 1 1 2

4 4 0 2 5 6

5 2 4 6

6 2 4 5

В программе эта структура реализована в массивах Vt, Adj, Nbr, Fst(табл. 1.1)/

 

Таблица 1.1

Vt [ x ]

Adj [ x ]

Nbr [ x ]

Fst [ x ]

 

Данное отображение структуры смежности позволяет обращаться к элементам массивов по номерам (меткам) соответствующих вершин.

Операция vÎ ADj [x] впрограммной реализациипредставляется какfor (i = 0; i < Nbr[ x ]; i ++) v = Adj [Fst [ x ] + i ] …, где Nbr[ x ] – количество вершин в структуре смежности для вершины x; Adj [ x ] – массив, содержащий списки смежности для каждой вершины; Fst [ x ] – номер первой вершины в списке смежности, соответствующем вершине x, тогда Fst [ x ] + i – номер i- й вершины в списке смежности, соответствующем вершине x. Например, пусть x = 3, тогда Fst [3] = 10 и Nbr [3] = 2 (в списке смежности вершины x два элемента), элементы Adj [ Fst [3] + 0] = Adj [10] = 1 и Adj [Fst [3] + 1] = Adj [11] = 2 составляют список смежности вершины x = 3.

Решение задачи начинается с вызова функции WayDepth, которая сначала помечает в массиве Mark все вершины как не пройденные (красит их меткой равной –1). Затем из вершин выбирается очередная (в порядке возрастания меток вершин) не пройденная вершина. Эта вершина рассматривается как корень дерева поиска в глубину, и для нее запускается функция Depth, реализующая проход графа в глубину. Функция Depth помечает в массиве Mark эту вершину как обнаруженную (красит ее значением целой переменной count, т.е. пройденные вершины постепенно нумеруются от 0 до │ V │ по мере того, как в них попадаем). Затем просматривается список смежности вершины, для которой запущена функция Depth. Если в этом списке есть еще не пройденные вершины (т. е. метка Mark [ v ] вершины v равна
–1), то ребро (x, v) добавляется к множеству основных ребер дерева поиска в глубину (вершины x и v помещаются в массив T). Процесс прохода графа в глубину в этом случае продолжается, начиная с не пройденной вершины v (для вершины v запускается функция Depth). Когда в списке смежности вершины x обнаружена пройденная вершина, то при Mark [ v ] ≠ –1 ребро
(x, v) будет обратным, если Mark [ v ] < Mark [ x ] и v ≠ s. Условие Mark [ v ] < Mark [ x ] означает, что вершина v была пройдена раньше вершины x. Поэтому ребро (x, v) будет обратным, если оно не является ребром дерева поиска, пройденным от предка s к x, т. е. v ≠ s.

Решение заканчивается, когда будут просмотрены все вершиныграфа(т. е. все элементы массива Mark станут отличны от –1).

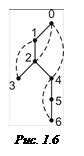
Дерево поиска в глубину для графа на рис. 1.5 имеет следующий вид (рис. 1.6): сплошными линиями отмечены ребра дерева, которые были пройдены во время обхода графа в глубину, штриховыми – обратные ребра. (На рис. 1.5 жирными линиями отмечены ребра, которые были пройдены во время обхода графа в глубину.)

Состояния рабочих массивов Mark, T и B после завершения алгоритма приведены в табл. 1.2:

 

Таблица 1.2