Таблица 3.12- Коэффициенты  и
и 
| Н1<350HB или H2<350HB | H1>35HRC или H2>35HRC | |
| Прямозубые колеса | 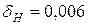 , , 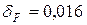
| 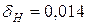 , , 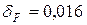
|
| Косозубые колеса |  , , 
|  , , 
|
Таблица 3.13 – Коэффициенты  и
и 
| Модуль m, мм | Степень точности | |||||
m 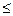 3,55 3,55
| ||||||
3,55< m 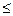 10 10
| ||||||
| m >10 | - |
 .
.
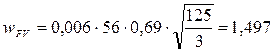 .
.
 .
.
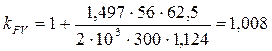 .
.
3.1.5 Проверка выполнения условия прочности по контактным напряжениям
Условие прочности по контактным напряжениям имеет вид

 ,
,
где  - действующее напряжение в контакте зубьев,
- действующее напряжение в контакте зубьев,
 - допускаемое напряжение в контакте зубьев
- допускаемое напряжение в контакте зубьев
 ; (3.28)
; (3.28)
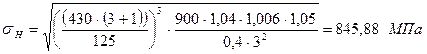 .
.
Проверяем по допускаемому напряжению
 МПа – Условие выполнено.
МПа – Условие выполнено.
3.1.6 Проверка выполнения условия прочности по напряжениям изгиба
Определяем эквивалентные числа зубьев шестерни и колеса
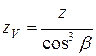 . (3.29)
. (3.29)
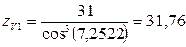 .
.
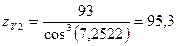 .
.
Определяем коэффициент формы зуба
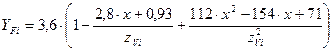 . (3.30)
. (3.30)
 .
.
 .
.
Определяем напряжение изгиба:
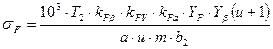 (3.31)
(3.31)
где kFa = 1 – коэффициент неравномерности нагружения зубьев;
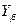 - коэффициент осевого перекрытия, определяется по формуле:
- коэффициент осевого перекрытия, определяется по формуле:
 .
.
Для шестерни:
 МПа
МПа
Для колеса:
 МПа
МПа
Условие прочности по напряжениям изгиба можно считать выполненным.
3.1.7 Определение геометрических параметров зубчатой передачи
Диаметры вершин зубьев шестерни и колеса
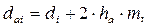 мм. (3.32)
мм. (3.32)
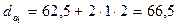 мм.
мм.
 мм.
мм.
Диаметры впадин зубьев шестерни и колеса
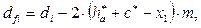 мм. (3.33)
мм. (3.33)
 мм.
мм.
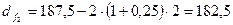 мм.
мм.
3.1.8 Определение сил в зацеплении
Окружная сила:
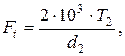 Н (3.34)
Н (3.34)
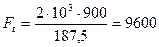 Н
Н
Радиальная сила:
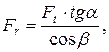 Н (3.35)
Н (3.35)
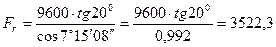 Н
Н
Осевая сила:
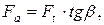 Н (3.36)
Н (3.36)
 Н.
Н.
3.2 Проектировочный расчет зубчатой конической ортогональной передачи с прямыми зубьями
Исходные данные:
Рассчитать зубчатую коническую прямозубую передачу одноступенчатого редуктора с моментом на выходе 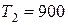 Н·м.
Н·м.
Частоты вращения входного и выходного валов передачи равны  об/мин и
об/мин и 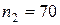 об/мин соответственно (передаточное число
об/мин соответственно (передаточное число  ).
).
Передача нереверсивная. Шестерня передачи расположена консольно относительно опор. Время безотказной работы 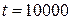 часов в тяжелом режиме нагружения.
часов в тяжелом режиме нагружения.
Зубчатые колеса изготовлены из стали 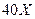 , закаленной по поверхности до твердости
, закаленной по поверхности до твердости 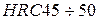 , термообработка типа «улучшение» с последующей закалкой ТВЧ по контуру до заявленной твердости.
, термообработка типа «улучшение» с последующей закалкой ТВЧ по контуру до заявленной твердости.
В качестве параметров исходного контура инструмента принять:
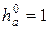 - коэффициент высоты головки зуба;
- коэффициент высоты головки зуба;
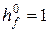 - коэффициент высоты ножки зуба;
- коэффициент высоты ножки зуба;
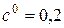 - коэффициент радиального зазора;
- коэффициент радиального зазора;
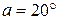 - угол профиля рейки.
- угол профиля рейки.
3.2.1 Определение допускаемых напряжений
Расчет допускаемых напряжений по контакту и по изгибу не зависит от типа зубчатой передачи. Поскольку исходные данные для расчета рассматриваемой конической передачи совпадают с аналогичными данными цилиндрической передачи (п. 3.1), то в качестве допускаемых напряжений можно принять значения, полученные в п. 3.1. Следовательно, имеем:
- допускаемое напряжение усталостной прочности по контакту:
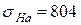 МПа;
МПа;
- допускаемые напряжения усталостной прочности по напряжениям изгиба:
для шестерни: 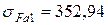 МПа;
МПа;
для колеса: 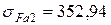 МПа.
МПа.
3.2.2 Расчет геометрии передачи из условия прочности по контактным напряжениям
На этапе проектировочного расчета, как и в п. 3.1, значение коэффициента динамичности нагрузки полагается равным  .
.
Коэффициент концентрации нагрузки 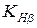 зависит от величины конструктивного коэффициента
зависит от величины конструктивного коэффициента  ,
,  , где
, где 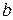 - ширина зубчатого венца. В свою очередь, для определения
- ширина зубчатого венца. В свою очередь, для определения  необходимо задать коэффициент ширины зубчатого венца
необходимо задать коэффициент ширины зубчатого венца 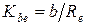 , значения которого лежат в диапазоне
, значения которого лежат в диапазоне 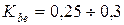 . Выбираем
. Выбираем  . Тогда для конструктивного коэффициента
. Тогда для конструктивного коэффициента  имеем
имеем
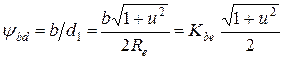 (3.37)
(3.37)
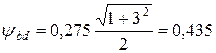
Используя данные табл. 3.5, для заданного по условию консольного размещения шестерни относительно опор получаем
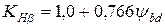 ,
,

Аналогично можно определить значение коэффициента концентрации нагрузки при расчете на изгиб 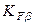 . Согласно табл. 3.9 запишем
. Согласно табл. 3.9 запишем
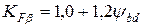
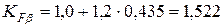
Внешний диаметр колеса  рассчитывается по формуле, полученной из условия прочности по допускаемым контактным напряжениям:
рассчитывается по формуле, полученной из условия прочности по допускаемым контактным напряжениям:
 мм (3.38)
мм (3.38)
где  - коэффициент изменения прочности,
- коэффициент изменения прочности, 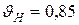 .
.
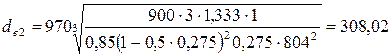 мм
мм
Внешний диаметр колеса 1
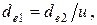 мм (3.39)
мм (3.39)
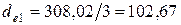 мм
мм
Следовательно, внешнее конусное расстояние конического зацепления 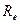 равно
равно
 мм (3.40)
мм (3.40)
 мм
мм
Для обеспечения выполнения геометрических и технологических условий изготовления конических передач количество зубьев шестерни вычисляется по следующей формуле
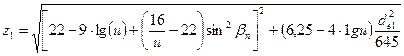 (3.41)
(3.41)
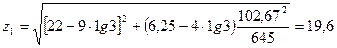 .
.
Поскольку количество зубьев шестерни может быть только целым числом, следовало бы принять  . Но, как покажут дальнейшие расчеты, для такого числа зубьев не будет выполняться условие прочности по контактным напряжениям, поэтому число зубьев нужно увеличить:
. Но, как покажут дальнейшие расчеты, для такого числа зубьев не будет выполняться условие прочности по контактным напряжениям, поэтому число зубьев нужно увеличить:  .
.
Расчетное значение внешнего окружного модуля равно
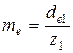 , мм (3.42)
, мм (3.42)
Следовательно, для передачи с прямым зубом имеем
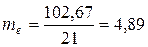 мм
мм
Полученную величину модуля 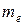 округляем, принимая ее равной ближайшему значению из нормального ряда (табл. 3.8), т.е. в данном случае
округляем, принимая ее равной ближайшему значению из нормального ряда (табл. 3.8), т.е. в данном случае  . Число зубьев колеса равно
. Число зубьев колеса равно
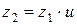 (3.43)
(3.43)

Зная  ,
, 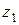 и
и  , можно получить уточненные значения диаметров шестерни и колеса:
, можно получить уточненные значения диаметров шестерни и колеса:
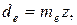 мм (3.44)
мм (3.44)
 мм
мм
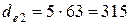 мм
мм
Тогда уточненное значение внешнего конусного расстояния конического зацепления равно:
 мм,
мм,
а значение рабочей ширины колеса:
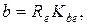 мм (3.45)
мм (3.45)
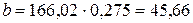 мм
мм
Полученное значение 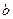 округляем до целого, т.е. полагаем
округляем до целого, т.е. полагаем 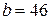 мм.
мм.
Теперь необходимо уточнить значение коэффициента ширины зубчатого венца:
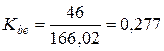 ,
,
а также пересчитать коэффициенты  ,
, 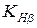 и
и 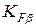 :
:
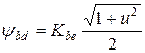 (3.46)
(3.46)
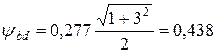
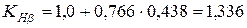 ;
;
 .
.
Среднее расстояние
 мм (3.47)
мм (3.47)
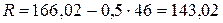 мм
мм
Средний окружной модуль
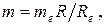 мм (3.48)
мм (3.48)
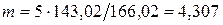 мм
мм
Средние делительные диаметры шестерни и колеса
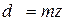 мм (3.49)
мм (3.49)
 мм
мм
 мм
мм
Угол делительного конуса шестерни
 (3.50)
(3.50)

Угол делительного конуса колеса
 .
.
Коэффициент смещения инструмента равносмещенной передачи (при 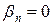 ):
):
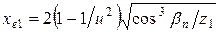 (3.51)
(3.51)

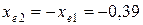
3.2.3 Расчет коэффициентов динамичности нагрузки
Далее переходим к определению коэффициентов динамичности нагрузки, значения которых зависят от скорости и степени точности изготовления передачи.
Вычисляем линейную окружную скорость  (3.23)
(3.23)
 м/с
м/с
Исходя из полученного значения скорости, можно выбирать рекомендуемую степень точности изготовления (табл. 3.11).
Поскольку на практике детали изготавливаются со степенью точности не ниже 8-й, то задаем степень точности равную 8.
Коэффициенты динамичности нагрузки при расчете контактных напряжений и напряжений изгиба, 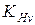 и
и 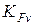 , рассчитываются по формулам (3.24) и (3.25) соответственно с учетом (3.26) и (3.27) и таблиц 3.12 и 3.13.
, рассчитываются по формулам (3.24) и (3.25) соответственно с учетом (3.26) и (3.27) и таблиц 3.12 и 3.13.
Получим  ;
; 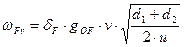 :
:
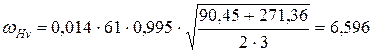 ,
,
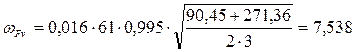 .
.
Тогда

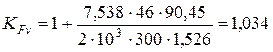 .
.
3.2.4 Проверка условий прочности по контактным напряжениям
Проверка сводится к определению величины действующего напряжения в контакте зубьев 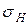 и сравнению его с полученным значением допускаемого напряжения
и сравнению его с полученным значением допускаемого напряжения 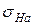 .
.
 , МПа (3.52)
, МПа (3.52)
Действующее напряжение
 МПа (3.53)
МПа (3.53)
 МПа.
МПа.
Очевидно, при таком значении действующего напряжения условие прочности по контакту оказывается выполненным
 МПа.
МПа.
3.2.5 Проверка условия прочности по напряжениям изгиба
Определяем приведенное число зубьев
 (3.54)
(3.54)

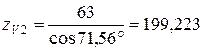
Определяем коэффициент формы зуба (3.30) для шестерни и колеса соответственно
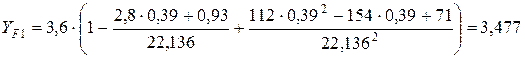
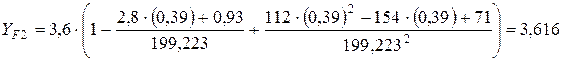
Используя полученные величины коэффициентов формы зуба, переходим к расчету напряжений изгиба и проверке изгибной прочности зубьев:
 (3.55)
(3.55)
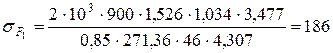 МПа
МПа
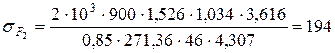 МПа.
МПа.
Поскольку
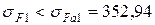 МПа
МПа
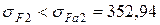 МПа,
МПа,
то условие прочности на изгиб можно считать выполненным.
3.2.6 Геометрический расчет передачи
Результаты геометрического расчета рассматриваемой передачи сведены в таблицу 3.14.
Таблица 3.14 - Параметры конической передачи
| Параметр | Обозначение, расчетная формула и величина | ||
| Число зубьев плоского колеса | 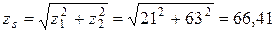
| ||
| Внешний окружной модуль, мм | 
| ||
| Внешнее конусное расстояние, мм | 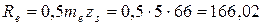
| ||
| Ширина зубчатого венца, мм | 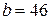
| ||
| Коэффициент ширины | 
| ||
| Сред. конусное расстояние | 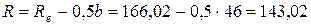
| ||
| Средний окружной модуль | 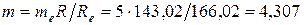
| ||
| Средний делительный диаметр | Шестерня | 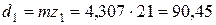
| |
| Колесо | 
| ||
| Передаточное число | 
| ||
| Угол делительного конуса | Шестерня | 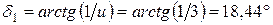
| |
| Колесо | 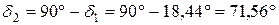
| ||
| Коэффициент смещения | Шестерня | 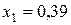
| |
| Колесо | 
| ||
| Внешняя высо- та головки, мм | Шестерня | 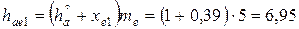
| |
| Колесо | 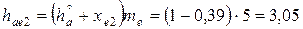
| ||
| Внешняя вы-сота ножки, мм | Шестерня | 
| |
| Колесо | 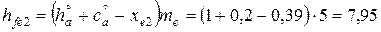
| ||
| Внешняя высота зуба, мм | Шестерня | 
| |
| Колесо | 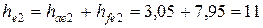
| ||
| Внешняя окружная толщина зубьев, мм | Шестерня | 
| |
| Колесо | 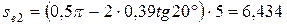
| ||
| Угол ножки зубьев | Шестерня | 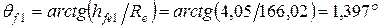
| |
| Колесо | 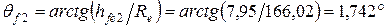
| ||
| Угол головки зубьев | Шестерня | 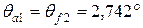
| |
| Колесо | 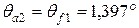
| ||
| Угол конуса вершин | Шестерня | 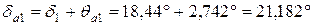
| |
| Колесо | 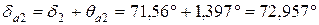
| ||
| Угол конуса впадин | Шестерня | 
| |
| Колесо | 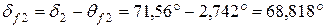
| ||
| Внешний делительный диаметр, мм | Шестерня | 
| |
| Колесо | 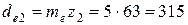
| ||
| Внешний диаметр вершин зубьев, мм | Шестерня | 
| |
| Колесо | 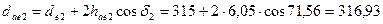
| ||
3.2.7 Силы в зацеплении
Определяем силы в контакте зубчатых колес.
Окружная сила (3.34)
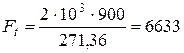 Н;
Н;
радиальная сила на шестерне
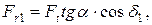 Н (3.56)
Н (3.56)
 Н;
Н;
осевая сила на шестерне
 , Н (3.57)
, Н (3.57)
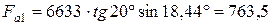 Н;
Н;
радиальная и осевая силы на колесе
 ,
, 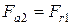 .
.
3.3 Проектировочный расчет червячной передачи
Исходные данные:
Рассчитать червячную передачу с архимедовым червяком, предназначенную для передачи крутящего момента с моментом на выходе 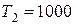 Н·м. Частота вращения на выходе
Н·м. Частота вращения на выходе 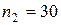 об/мин, передаточное число
об/мин, передаточное число 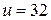 .
.
Время безотказной работы передачи – 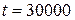 часов. Режим работы - тяжелый. Температура окружающей среды
часов. Режим работы - тяжелый. Температура окружающей среды 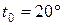 С.
С.