Лабораторная работа №5. Тема: «Полнота систем булевых функций»
(Теория и примеры – в мет-ке).
Основные понятия
Пусть B — некоторое множество функций алгебры логики. Замыканием [ B ] множества B называется совокупность всех функций из Р2, являющихся суперпозициями функций из множества B. Множество B называется замкнутым классом, если [ B ]= B. Пусть B – замкнутый класс в Р 2. Множество B называется функционально полной системой в Р2, если [ B ] = Р2.
Множество B называется предполным классом в Р2, если оно не является полной системой в Р2, но для всякой функции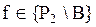 
выполняется равенство 
Замкнутые классы Поста
1. Говорят, что функция 
сохраняет константу 0, если f(0,0,...,0)=0.
T0 − класс функций, сохраняющих ноль:
T0 = {f Î P2 ç f (0,0,...,0) = 0}.
2. Говорят, что функция 
сохраняет константу 1, если f (1,1,...,1)=1.
T1 − класс функций, сохраняющих единицу:
T1 = {f Î P2 ç f (1,1,...,1) = 1}.
3. Функция 
называется двойственной к 
, если на противоположных наборах она принимает противоположные значения, т.е.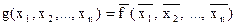 
. Двойственная функция обозначается 
.
Функция 
называется самодвойственной, если она совпадает со своей двойственной функцией. S -- класс самодвойственных функций :
S = {f Î P2 ç f (a1,a2,...,an) = 
(
, 
,..., 
) }.
4. Для двоичных векторов 
и 
, где i=1,2,…,n, введем следующее отношение 
частичного порядка, называемое отношением предшествования. Будем говорить, что набор 
предшествует набору 
и писать 
, если ai≤bi для всех i=1,2,…,n. Функция f(x1,x2,…,xn) называется монотонной, если для любых векторов 
, находящихся в отношении предшествования , выполняется соотношение 
.
М − класс монотонных функций: М ={ f Î P2 (n) çf − монотонна}.
5. L − класс линейных функций составляют функции, которые представляются полиномом Жегалкина первой степени:
L={ f Î P2 (n) çf = k0Åk1x1 Åk2x2 Å … Åknxn }, где kiÎ{0,1}.
Проверка принадлежности булевой функции замкнутым классам 1-4 осуществляется по таблице истинности. Проверка принадлежности булевой функции классу L осуществляется путем построения многочлена Жегалкина.
Каждое из множеств T 0, T 1, S, L, M является замкнутым и предполным классом в P 2.
Критерий полноты системы булевых функций
Теорема Поста. Система булевых функций В функционально полна в Р 2 тогда и только тогда, когда она содержит:
хотя бы одну функцию, не сохраняющую ноль,
хотя бы одну функцию, не сохраняющую единицу,
хотя бы одну немонотонную функцию,
хотя бы одну несамодвойственную функцию
и хотя бы одну нелинейную функцию.
Для проверки функциональной полноты системы булевых функций строится так называемая таблица Поста, в которой отмечается принадлежность функций замкнутым классам. Если в каждом столбце таблицы Поста есть хотя бы один минус, система полна, в противном случае – нет.
Пример. Проверить систему булевых функций В = {x Å y, x Ù y,1} на функциональную полноту.
Проверим принадлежность замкнутым классам функции f (x, y) = x Å y. Построим таблицу истинности данной функции.
f (0,0) = 0, следовательно f (x, y) ÎT0.
f (1,1) = 0, следовательно f (x, y)Ï T1.
f (0,0) = f (1,1), следовательно, f (x, y) ÏS.
f (1,0) = 1 > 0 = f (1,1), следовательно, f (x, y) ÏM.
Функция представляет собой полином Жегалкина первой степени, следовательно, f (x, y) Î L.
Результаты заносим в первую строку таблицы Поста. Остальные функции исследуются аналогично. Окончательно таблица Поста имеет вид:
В каждом столбце таблицы имеется минус, следовательно, система В функционально полна.
Ответ: система В полна.
Задание к теме 5. С помощью теоремы Поставыяснить, полна ли заданная система булевых функций.
Если ДА, то
· выразить константы, отрицание и конъюнкцию через функции этой системы, (т.е. провести поэтапное доказательство теоремы Поста);
· найти все базисы в системе.
Варианты
1. 
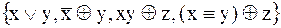
2. 
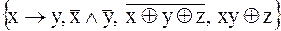
3. 
4. 
5. 
6. 
7. 
8. 
9. 
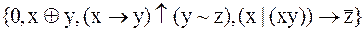
10. 
11. 
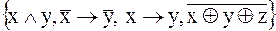
12. 
13. 
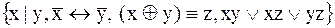
14. 
15. 
16. 
17. 
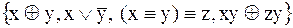
18. 
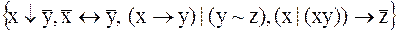
19. 
20. 
21. 
22. 
23. 
24. 
25. 