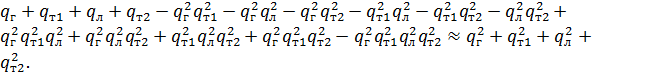Для количественной оценки различных показателей надежности используют понятия случайного события, случайной величины и случайного процесса.
Случайные события. Случайным событием называется событие, которое может в данных конкретных условиях или произойти или нет. Для количественного сравнения событий между собой по степени их возможности с каждым событием связывают определенное число. Это число называется вероятностью события.
В качестве единицы измерения степени возможности события принятия вероятность достоверного события, т.е. такого события которое в результате опыта непременно должно произойти никогда. Вероятность появления достоверного события принимается равной единице. Противоположным по отношению к достоверному событию является невозможное событие, т.е. такое событие, которое в данном опыте не может произойти. Вероятность его появления принимается равной нулю. Таким образом, диапазон изменения вероятностей любых событий – числа от 0 до1.
Несколько событий образуют полную группу событий, если в результате опыта должно произойти хотя бы одно из них. События называются несовместными, если они не могут появиться вместе. И наоборот, события называются совместными, если они могут появиться одновременно. Если вероятность одного события не изменяется от того, произошло или не произошло другое событие, то такие события называется независимыми. Если же вероятность появления одного события зависит от того, произошло или не произошло другое событие, то такие события называются зависимыми.
Суммой нескольких событий Ai называется сложное событие, состоящее в появлении хотя бы одного из простых событий, составляющих его.
Теорема сложения вероятностей формулируется следующим образом.
Вероятность суммы несовместных событий равна сумме вероятностей этих событий.
| (2.1) |
Если события A и B совместны, то вероятность суммы этих событий выражается формулой
| (2.2) |
где P(AB) – вероятность совместного появления событий A и B.
Эта теорема имеет два следствия.
Следствие 1. Если события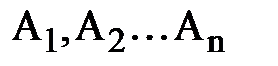 
образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
| (2.3) |
Следствие 2. Сумма вероятностей противоположных событий равна единице.
| (2.4) |
Под противоположными событиями понимают два события, образующих полную группу событий.
Произведением нескольких событий Ai называется сложное событие, состоящее в совместном появлении всех составляющих его событий. Теорема умножения вероятностей формулируется следующим образом. Вероятность произведения независимых событий равна произведению вероятностей этих событий.
| (2.5) |
Вероятность произведения двух зависимых событий A1 и A2 равны произведению вероятности одного из них на условную вероятность другого.
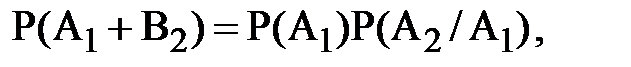
| (2.6) |
Здесь 
- вероятность события A2, вычисленная при условии, что имело место событие A1.
Показатели надежности
Показателем надежности называется количественная характеристика одного или нескольких свойств, определяющих надежность объекта. Их подразделяют на единичные, характеризующие одно свойство, и комплексные, характеризующие несколько свойств. Единичные применяются в основном для характеристики отдельных конструктивных элементов, комплексные - для узлов нагрузки и систем в целом.
Единичные показатели.
Вероятность безотказной работы 
это вероятность того, что время работы объекта до отказа 
будет не меньше заданного времени t
| (3.1) |
Вероятность отказа 
это вероятность того, что отказ наступит до момента t
| (3.2) |
и 
образуют полную группу событий и согласно следствию из теоремы сложения вероятностей
| (3.3) |
Под структурой надежности понимают результирующую надежность системы при заданной ее структуре. Система при этом рассматривается, как абстрактная структура вне зависимости от ее физической природы, но обладающая общими закономерностями:
- имеет вход и выход;
- показатели надежности определяются на выходе системы;
- все элементы находятся только в двух состояниях (работоспособном и неработоспособном);
- отказы элементов являются независимыми событиями, а поток отказов ординарен;
- время безотказной работы много больше времени восстановления элементов.
Показатели структурной надежности имеют смысл определять в первую очередь для отдельных узлов (групп узлов) нагрузки (потребителей), т.е. для отдельных объектов системы электроснабжения. Этим и диктуется состав определяемых показателей.
При оценке структурной надежности целесообразно ввести понятие «расчетный элемент» системы, которое может быть отлично от понятия «элемент» системы. Под расчетным элементом в смысле надежности понимается физический объект (группа объектов) электрической системы, отказ которого снижает уровень надежности системы. Под элементами чаще всего понимаются отдельные электрические машины и аппараты: генераторы, трансформаторы, выключатели, разъединители, отделители, короткозамыкатели, сборные шины РУ. Несколько условно к элементам относят также линии электропередач. Часто для уменьшения числа элементов в расчетной схеме системы и упрощения расчетов за элемент принимается «присоединение», т.е. совокупность оборудования, необходимого для присоединения линий, трансформаторов, генераторов, ряд последовательно соединенных элементов в цепи передачи энергии (линия, выключатель, трансформатор) или группа зависимых элементов (двухцепная ЛЭП).
Для определения характеристик надежности систем электроснабжения p(t) и g(t) составляется структурная схема (блок-схема), в которой каждый элемент расчета надежности представляется квадратом, внутри которого указывается его порядковый номер (рис. 1, а). Расчет надежности по блок-схеме проводится путем ряда преобразований последовательно или параллельно включенных блоков в эквивалентные (рис. 1, б и 1, в) до тех пор, пока шины источника питания и пот потребителя не окажутся связанными одним эквивалентам блоком. Показатели надежности этого блока (рис.1, г) и являются искомыми показателями надежности электроснабжения потребителя.
Рис.1. Структурная блок-схема для расчета надежности (а) и ее преобразование (б, в и г)
Соединение блоков между собой сводится, в конечном счете, к последовательному и параллельному соединениям. Рассмотрим определение показателей надежности p(t) и g(t) для этих схем соединений.
Последовательное соединение. На рис.2 показана блок-схема, состоящая из блоков, соединенных последовательно. Такая схема будет выполнять заданные функции при условии, что все ее элементы будут исправны. Если значения надежности отдельных блоков схемы не зависят друг от друга, то, согласно теореме умножения, вероятность безотказной работы схемы определится как произведение значений надежности для отдельных ее частей, т.е.
| (3.4) |
 а)
|
б)
Рис. 2. Блок – схема из последовательно соединенных элементов расчета надежности
Рассматриваемая система откажет, если откажет хотя бы один ее элемент. Этот вывод позволяет применить для определения вероятности отказа системы 
теорему сложения вероятностей. Однако, чтобы уменьшить объем вычислений, целесообразнее для нахождения использовать соотношение (3.3) согласно которому
| (3.5) |
Параллельное соединение. На рис. 3 приведена блок-схема, состоящая из n параллельно соединенных элементов, m элементов обеспечивают нормальное функционирование системы, а n-m являются постоянно включенным горячим резервом. Считается по-прежнему, что надежность каждого из блоков не зависит от отказа любого другого блока. Такая система откажет, если одновременно откажет n-m + 1 элемент, т.е. откажут все резервные элементы и еще один. Согласно теореме умножения вероятностей вероятность отказа такой системы может быть определена из выражения:
| (3.6) |
Надежность работы схемы может быть определена, согласно (3.3), из выражения:
| (3.7) |
Рис. 3. Блок – схема из параллельно соединенных элементов расчета надежности
Примеры решения задач
Пример 1
Электрическая станция состоит из трех основных частей: котла, турбины и генератора. Известны вероятности отказов каждого из этих элементов:
- вероятность отказа котла qK =0,02;
- вероятность отказа турбины qT =0,01;
- вероятность отказа генератора qГ = 1 - 0,001.
Определить вероятность безотказной работы электростанции P100 и вероятность отказа электростанции (прекращение выработки и электроэнергии) P0.
1. Составляем логическую блок-схему электростанции
Рис. 4. Блок – схема электростанции
2. Вероятность безотказной работы элементов блок-схемы определяется согласно следствия теоремы сложения вероятностей:
PK= 1 - qK= 1 - 0,02 = 0,98;
PT= 1 - qT= 1 - 0,01 = 0,99;
PГ = 1 - qГ = 1 - 0,001 = 0,999;
3. Вероятность безотказной работы электростанции на основании теоремы умножения вероятностей:
P100 = PK*PT*PГ = 0,98*0,99*0,999 = 0,9692298;
Вероятность отказа электростанции:
P0 = 1 - P100 = 1 – 0,9692298 = 0,0307702;
ВероятностьP0 может быть найдена и другим путем с единовременным применением теории сложения и умножения вероятностей:
P0 = qK*PT*PГ + PK*qT*PГ + PК*PТ*qГ + qК*qТ*PГ + qК*PТ*qГ + PK*qT*qГ + qК*qТ*qГ
Пример 2
Две линии электропередачи включены на параллельную работу.
Рис. 5. Электрическая схема.
Потребитель получает электроэнергию по обоим линиям одновременно. Пропускная способность каждой линии 100%, т.е. каждая линия может передать потребителю всю необходимую ему электроэнергию. Вероятность выхода из строя одной линии qл1=qл2=qл.
Определить вероятность передать потребителю 100% P.
Составим блок-схему.
Рис. 6. Блок – схема.
Схема отк. если отк. обе линии одновременно P0=qл1*qл2=qл2.
Потребитель получит 100% мощности если работает хотя бы одна из линий P100=Pл1*qл2+Pл2*qл1+Pл1*Pл2=1-P0
Пример 3
Условия те же, что и в задаче 2, но каждая линия может передать только 50% требуемой потребителю мощности. Определить вероятность передачи потребителю 100% мощности 
, отказ схемы 
и передачи только 50% мощности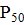 
.
Потребитель получит 100% мощности, если обе линии находятся в работе
т.к. 
.
Потребитель получит 50% мощности если в работе находится одна из линий, а другая линия отключена
Потребитель получит 0% мощности, если откажут обе линии одновременно
или 
Пример 4.
Система передачи электроэнергии (рис. 7, а) потребителю состоит из генератора Г, повышающего трансформатора TI, линии электропередачи Л и понижающего трансформатора T2. Вероятности повреждения элементов передачи gГ=2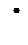 
10-3, gТ1=5 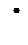10-5, gЛ=2 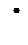10-3, gТ2=4 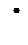10-5. Требуется определить вероятность того, что потребитель не получит электроэнергии из-за повреждения системы, считая события повреждения элементов независимыми друг от друга.
Для безотказной работы системы необходимо, чтобы генератор, повышающий и понижающий трансформаторы и линия электропередач, работали безотказно. Таким образом, сложное событие – имеет место при совмещении четырех составляющих его простых событий. Блок-схема рассматриваемой системы передачи электроэнергии приведена на рис. 7, б. Согласно теореме умножения вероятностей, вероятность безотказной работы системы
|
Поврежденные системы является противоположным событием безотказной ее работе. Поэтому
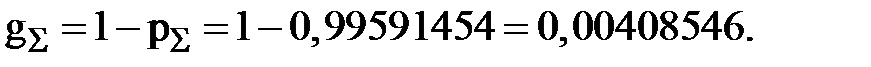
Рис. 7 Электрическая сеть а) и блок – схема для расчета надежности б)
Пример 5.
Пусть статистическая вероятность повреждений любой фазы линии составляет 0,001. Примем также, что если повреждение одной фазы произошло, то повреждение другой любой фазы будет иметь статистическую вероятность 0,2, т.е условная вероятность повреждения второй фазы при повреждении первой равно 0,2. Кроме того, пусть аналогичные вероятности повреждения третьей фазы при повреждении двух других составляют 0,5. Определим соотношения вероятности однофазных, двухфазных и трехфазных коротких замыканий при условии, что авария началась с повреждения одной фазы.
Вероятность аварийного повреждения двух фаз:
P2=0,2*0,001=0,0002
Вероятность аварийного повреждения трех фаз:
P3=0,5*0,002=0,0001
Пример 6.
Система передачи электроэнергии состоит из повышающего трансформатора Т1 (рис. 8), двух цепей линии электропередачи Л и двух понижающих трансформаторов Т2.По любой цепи потребитель может получить всю необходимую ему мощность. Но понижающий трансформатор может пропустить только 50 % мощности. Вероятность повреждения трансформатора Т1 qт1 = 0,005, одной цепи Л qл = 0,03, одного понижающего трансформатора qт2 = 0,006. Повреждения всех элементов следует считать независимыми случайными событиями. Предполагая, что передается постоянная мощность, определить вероятность передачи 100, 50 и 0% мощности.
Рис. 8 Система передачи электроэнергии с одним повышающим трансформатором
Решение: 1) Вероятность передачи 100% мощности (условия Т1 не поврежден, хотя бы одна цепь Л в работе и не повреждены два трансформатора Т2):
2) Вероятность передачи 50% мощности (условия Т1 не поврежден, хотя бы одна цепь Л в работе поврежден один из трансформаторов Т2)
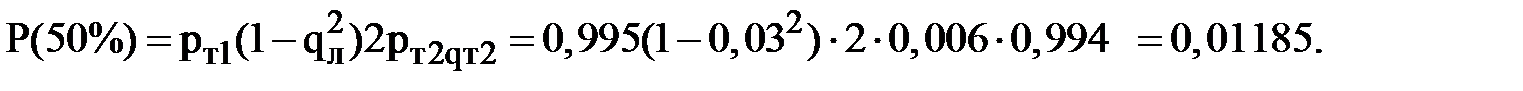
3) Вероятность полной потери электроснабжения потребителя равна сумме вероятностей повреждения трансформатора Т1, двух цепей Л и двух понижающих трансформаторов Т2:
Пример 7.
Потребитель получает электроэнергию от двух генераторов Г, двух повышающих и понижающих трансформаторов Т1, Т2, двух линий электропередачи Л (рис. 6-4). По каждой линии и каждому повышающему трансформатору можно передать 100% мощности, необходимой потребителю.
Рис. 9. Система передачи электроэнергии с двумя повышающими трансформаторами
Пропускная способность понижающего трансформатора 50% общей мощности. Каждый генератор выдает в систему только 50% необходимой мощности. Считая повреждения отдельных элементов системы 
, 
, 
, 
независимыми событиями, определить вероятность передачи:
1) 100%, 2) 50%, 3) 0% мощности потребителю.
Решение: 1) 
2) P (50) = 
3) P(0)= 