ВЫЧИСЛЕНИЯ ПО ФОРМУЛАМ. РАЗВЕТВЛЕНИЯ. ЦИКЛЫ.

ВВЕДЕНИЕ

 

Предлагаемые в сборнике задачи сгруппированы по следующим темам:

- программирование линейных, разветвляющихся, циклических алгоритмов; программирование алгоритмов, вычисляющих сумму, количество значений функции; вычисление минимального, максимального значений функций; вычисление суммы бесконечного ряда;

- программирование алгоритмов обработки одномерных массивов: различные сортировки, вычисление максимума, минимума, суммы и количества элементов массива, перестановка элементов;

- программирование алгоритмов обработки двухмерных массивов: суммы элементов матрицы, сумм элементов матрицы по строкам и столбцам, количество и суммы элементов, удовлетворяющих некоторому условию, перестановка строк, столбцов, циклические перестановки различного вида;

- программирование алгоритмов с использованием процедур и функций;

- программирование алгоритмов обработки записей и файлов;

- программирование рисунков с использованием графических средств.

Формулировка задач универсальна в том смысле, что для написания программ могут использоваться разнообразные языки программирования, а сами программы могут выполняться на разных вычислительных машинах.

Сборник заданий может быть использован при проведении лабораторных работ по программированию, информатике и вычислительной технике, экономической информатике в качестве учебного пособия, а также при проведении учебно-вычислительного практикума дневной и безотрывной форм обучения.

Задания для учебно-вычислительного практикума студенты безотрывного обучения должны выбирать в соответствии с двумя последними цифрами своего учебного номера (шифра) по следующему правилу: последняя цифра номера варианта должна совпадать с последней цифрой шифра. Далее, если предпоследняя цифра шифра четная, то и предпоследняя цифра варианта задания должна быть четной; если же предпоследняя цифра нечетная, то и предпоследняя цифра номера задачи должна быть нечетной. Если номер варианта однозначный, то перед ним надо поставить ноль. Например, при учебном номере (шифре) 176 студент выполняет вариант заданий, у которых последняя цифра номера 6, а предпоследняя - нечетная, т.е. вариант 16. Если номер (шифр) 106, то выбирается вариант 6. При шифре 146 также вариант 6.

ВЫЧИСЛЕНИЯ ПО ФОРМУЛАМ. РАЗВЕТВЛЕНИЯ. ЦИКЛЫ.

 

Задание 1

а) Дано: х = 2,6; y = -3,1. Вычислить: , если и .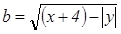

б) Дано: a = -0,5; b = 2. Вычислить: z= 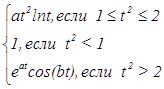для

t = 0,324; t = 1,76.

в) Представить таблицу значений аргумента и заданной функции.

, где z = cos(3x² – x + 1) для х [2;8] с шагом 0,5.

Задание 2

а) Дано: a = 1,5; b = 0,7; c = 2.

Вычислить: z = sin(xy) + 2, где , y = ln(a) – bc.

б) Вычислить: y= ,

для х = 2,2; х= -5,3.

в) Представить таблицу значений аргумента и заданной функции.

, где b = e^(x+2) + 0,6; c = x² – 1 для x [-7;2] с шагом 2.

Задание 3

а) Дано: a = -2,7; b = 4,1. Вычислить: y = xt - ln|xt|,

где x = 2sin(a²b) - cos , .

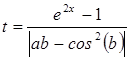б) Вычислить: y = e^z + lg|z|, для x=0,5; x=-2,73.

в) Представить таблицу значений аргумента и заданной функции 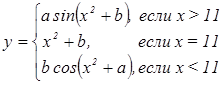, где a = 2tg(x); b = arctg - 4 для х [7;17] с шагом h = 2.

Задание 4

а) Вычислить: p = ; S = , где c = 5,2; a = 0,13; b=0,8.

б) Вычислить: y = e^z + 3,5 - cos³(xz), z = , для х = 3; x = 5,2.

в) Представить таблицу значений аргумента и заданной функции.

y = , где d = 13e^t; a = 0,5t³ - sin(t); b = 1,5t - |t|^1/3 для t [-3,2;4,5] с шагом 0,9.

Задание 5

а) Вычислить: y = 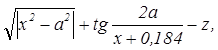где z = для a = 121,3; x = 0,75; s = 0,393.

б) Вычислить: y = где a = 15,631; b = 3,084; x = 0,194.

в) Представить таблицу значений аргумента и заданной функции.

z = , где a = cos(y - 1) для у [-1;2] c шагом 0,3.

Задание 6

а) Дано: a = -1,7; b = 2,4. Вычислить: z = e^x - sin²(x + y), где

x = , y = ln(b+2).

б) Вычислить: y = , p = 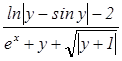для x = 1,2;

х = -1,2; х = 3,2.

в) Представить таблицу значений аргумента и заданной функции.

, где x = cos²(u - 2); b = sin(u - 2)²

для u [-3,39;5,86] c шагом 0,93.

Задание 7

а) Дано: z = 5,2; t = 6,7; c = -2,5. Найти: 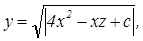где x = .

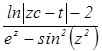б) Вычислить: z = e^cos(xy) – 2,7y; y = при x = -2; x = 7,5.

в) Представить таблицу значений аргумента и заданной функции

y = , где z = для х [4;6] с шагом 0,2.

Задание 8

а) Дано: x = 2,1; y = -1,7. Вычислить: p = , где

a = cos³|xy| - 1, b = e^xy - |y|sin(x).

б) Вычислить: z = , где t = -0,438; a = 2;

b = 0,789.

в) Представить таблицу значений аргумента и заданной функции

, где а = 12|x - 1|^1/5; b = (x - 2)²+4cos(x)

для x [-7;18] c шагом 2,3.

Задание 9

а) Вычислить: z = , где a = -x + bx², y =

при x = 1,5; b = 1,2.

б) Вычислить: z = , y = при x = 2,7;

x = 1,4.

в) Представить таблицу значений аргумента и заданной функции

y = , где a = x² - 6x - 1, b = для х [-3;6] с шагом 0,8.

Задание 10

а) Дано: x = 5,8; y = -4,2. Вычислить: c = , где

a = cos²(y) - ln(x), b= .

б) Вычислить: s = , где a = 5,89;

b = -0,673.

в) Представить таблицу значений аргумента и заданной функции.

, где b = 0,01x + e^0,7, c = + ln|x|

для x [-3;2,4] с шагом 0,8.

Задание 11

а) Дано: a = -0,7; b = 2,7. Вычислить: с = e^x – y - |x + y|, где x = ,

y = 3cos²(a - 2).

б) Вычислить: для x = 1,18; a = 1,3;

b = -1,5; c = 2,84.

в) Дано: a = 0,5; x [5;10] с шагом h = 1. Вычислить: ,

.

Задание 12

а) Дано: x = 7,2; y = 5,4. Вычислить: , где , .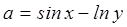

б) Вычислить: z = для a = 1,4;

x = -3,27.

в) Вычислить: 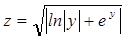; , где y [-2,8;0,2] с шагом 0,5; x = -2,4; b = 6,2.

Задание 13

a) Вычислить: , где ;

x = ; t = -0,324; a = -0,5; b = 1,3.

б) Вычислить: z = , y = для x = 1,5; x = -3;

x = 0,8.

в) Вычислить: y = , s = если

t [-0,3;0,5] с шагом 0,2 при а = 2,3; b = -4,1.

Задание 14

а) Вычислить: , где при

a = 0,5; b = 1,3.

б) Вычислить , y =

для x = 4; x = -2; x = 0,8.

в) Вычислить: , y = z² - tg(a + 4), если x [0,2;14] с шагом 2,2; a = 1,6.

Задание 15

а) Вычислить: y = при a = 2,3sin(t); b = 17,6x³; t = 3;

x = 1,38.

б) Вычислить: при a = 13,7; b = 8,91; x=0,07.

в) Вычислить: 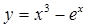; 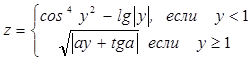, если x [4;8] с шагом 0,5; a = 3,4.

Задание 16

а) Вычислить: , где при x = 1,7; b = -1,2.

б) Вычислить: z = ; c = для x = -2;

x = 1,7; x = 0,4.

в) Вычислить: ; y = ,

где t [-0,5; 2,5] с шагом h = 0,5; b = 0,2.

Задание 17

а) Вычислить: 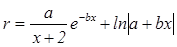, где a = tg(x) – 2,173x при x = 0,3;

b = 2,9.

б) Вычислить: y = при а = 5,08;

b = 0,08; x = -1,793.

в) Вычислить: z = ; r= , если у [ 1,2;2,4] с шагом h = 0,2; a = 2,7; b = -2.

Задание 18

а) Вычислить: s = , где a = , при x = 0,57;

b = 2,87.

б) Вычислить: y =

при a = 5,08; b = -3,194; x = 0,83.

в) Вычислить: y = ; z = ,

если x [-2,7;-1,8] с шагом h = 0,1; c = -0,4.

Задание 19

а) Вычислить: y = a×e^-xcos(bx) + c, где a = 2sin(x) + 0,56; c =

при x = 2,3; b = 2.

б) Вычислить: z = , для a = -2,34; i = 7;

b = 0,5.

в) Вычислить: y = x² - 2sin(x); z = 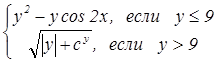при x [2;4] с шагом 0,2; c = 0,3.

Задание 20

a) Вычислить: y = 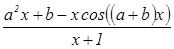, где a = bx + 17,3 для b = 0,9;

x = 0,384.

б) Вычислить: y = при a = 2,2; b = 0,3;

i = 6.

в) Вычислить: z = ; y = ,

если x [0,4;2,6] с шагом h = 0,2; a = 6,2; b = 4,7.

Задание 21

а) Вычислить: f = e^2x (a+x) - |b|^3x , где b = a² - x²sin(x) при a = 0,5;

x = 2.

б) Вычислить: z = , r = 2lg|z|+ln

для t = 1,5; t = -0,4; t = 0,5.

в) Вычислить: y = ; t = cos³y;

z = , при x [1,1;2,1] с шагом h = 0,2; a = 3,1.

Задание 22

а) Вычислить: z = 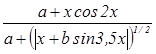, где a = 1,78×lnx² - 0,83cosx²

при x = 2; b = -4,7.

б) Вычислить: s = для t = 4,3; a = 2,87

в) Вычислить: z = ; y = lg(z²) - a× z

при x [0,2; 2,4] с шагом h = 0,2; a = 1,5.

 

Задание 23

а) Вычислить: , где c = b×cos(x/4) – 0,78x³ при x= 3,4; a= 1,12; b= -3,24.

б) Вычислить: z = для a = 1,3; x = 0,138.

в) Вычислить: ; z =

при x [0,1; 2,4] с шагом h = 0,2; a = 1,2; b = 1,4.

Задание 24

а) Вычислить: , где b = ln(a)- при x = 1,8;

a = 2,1.

б) Вычислить: y = при a = -2,391;

b = 7,08; x = 0,023.

в) Представить таблицу значений аргумента и заданной функции

y = , где a = ln(t² + 2t + 5); b = cos²t – sin(t) для t [2; 6]

с шагом 0,5.

 

Задание 25

а) Вычислить: , где a = e^-bx - tg(b+x) при x= -0,41;

b= 0,5.

б) Вычислить: z = , для b= 1,38; x= 5,83.

в) Вычислить: x = , y =

для t [-2,8;-2] с шагом 0,1; b= 2,2.