Практическое занятие №10.

Практическое занятие №9.

Магнитные и нелинейные цепи

Вопросы для подготовки к занятиям

Магнитные цепи с постоянным намагничивающим током

1. Для чего сердечники электрических машин и аппаратов изготавливают из ферромагнитных материалов?

2. Дать понятие об однородной и неоднородной, разветвленной и неразветвленной магнитной цепи.

3. Закон полного тока для однородной и неоднородной магнитной цепи.

4. Алгоритм решения прямой и обратной задачи для однородной магнитной цепи.

5. Алгоритм решения прямой задачи для неоднородной магнитной цепи.

6. Алгоритм решения обратной задачи для неоднородной магнитной цепи

7. Как изменится индуктивность катушки при уменьшении длины воздушного зазора?

8. Как изменится ток в катушке при увеличении длины воздушного зазора?

9. Как изменится магнитный поток в сердечнике, если воздушный зазор заполнить прокладкой из ферромагнитного материала?

10. Как нужно изменить магнитодвижущую силу катушки, чтобы сохранить неизменным магнитный поток при увеличении длины воздушного зазора?

11. Как изменится индуктивность катушки, если в воздушный зазор положить ферромагнитную пластину?

Магнитные цепи с переменным намагничивающим током

1. Какова форма тока в катушке и магнитного потока в сердечнике при синусоидальном приложенном напряжении?

2. Привести схему замещения и векторную диаграмму идеализированной катушки с сердечником (R = 0, X_p = 0).

3. Какие процессы в идеализированной катушке учитывают параметры ее схемы замещения?

4. Привести схему замещения и векторную диаграмму реальной катушки с сердечником.

5. Какие процессы в реальной катушке учитывают параметры ее схемы замещения?

6. Записать уравнение электрического равновесия для катушки с ферромагнитным сердечником и без него.

7. Зависит ли ток в катушке с ферромагнитным сердечником от материала сердечника и от наличия в нем воздушного зазора?

8. Как изменится амплитуда магнитного потока при увеличении длины воздушного зазора в сердечнике?

9. Как изменится ток в обмотке дросселя при увеличении длины воздушного зазора в сердечнике?

10. Как изменится индуктивность обмотки дросселя, если воздушный зазор в сердечнике заполнить ферромагнитной прокладкой?

11. Как изменится полное сопротивление обмотки дросселя, если увеличить длину воздушного зазора в сердечнике?

12. Зависит ли активная мощность, потребляемая из сети (активное сопротивление обмотки принять равным нулю) от величины приложенного напряжения?

13. Зависит ли потребляемая дросселем из сети активная мощность (при сопротивлении обмотки R = 0) от частоты источника питания?

14. Зависит ли потребляемая дросселем из сети активная мощность (при сопротивлении обмотки R = 0) от длины воздушного зазора в сердечнике?

15. Как изменится ток в обмотке дросселя при увеличении приложенного напряжения?

16. Как изменится индуктивность обмотки дросселя, если увеличить длину воздушного зазора в сердечнике?

Примеры решения прямой и обратной задачи

Пример 1

Рассмотрим магнитную цепь на рис. 9.1.

Рис. 9.1. Магнитная цепь. Рис. 9.2. Кривая намагничивания стали

Пусть необходимо создать Ф = 0,0165 Вб. Определить IW =?

Задана кривая намагничивания стали (рис. 9.2) из которой выполнены ферромагнитные участки изображенного контура магнитной цепи (рис. 9.1).

Решение. Используя рис. определяем геометрические размеры участков L₁ = 0,975 м, L₂ = 0,82 м, δ = 0,002 м, S₁ = 0,15 × 0,15 = 0,0225 м², S₂ = 0,1 × 0,15 = 0,015 м², S_δ = 0,1 × 0,15 = 0,015 м².

Определим величину магнитной индукции на каждом участке

B₁ = Ф / S₁ = 0,0165 / 0,0225 = 0,735 Тл;
B₂ = Ф / S₂ = 0,0165 / 0,015 = 1,1 Тл;
B_возд = Ф / S_δ = 0,0165 / 0,015 = 1,1 Тл.

Пользуясь кривой намагничивания для литой стали, определим напряжение магнитного поля в первом и во втором участках магнитной цепи:

H₁ = 350 А/м; H₂ = 940 А/м.

Напряженность в воздушном зазоре определяем из соотношения

H_возд = 8 × 10⁵ × B_возд = 8 × 10⁵ × 1,1 = 8,8 × 10⁵ А/м.

Искомая намагничивающая сила обмотки

F = H₁ L₁ + H₂ L₂ + H_возд δ = 350 × 0,975 + 940 × 0,82 + 8,8 × 10⁵ × 0,002 = 2870 АВ.

Обратим внимание на то, что 60% намагничивающей силы затрачивается на поддержание магнитного потока в воздушном зазоре, в то время как ширина зазора δ составляет < 0,15 % от общей длины магнитной цепи (b1 + b2 + δ). Этот факт является характерным для всех магнитных цепей и заставляет конструкторов электрических машин (во избежании чрезмерного увеличения намагничивающих сил обмоток) делать в магнитных цепях ширину воздушных зазоров возможно малой.

Пример 2

Определить магнитный поток в воздушном зазоре магнитопровода (рис. 9.1), если намагничивающая сила обмотки F = 2000 A. Значения величины L₁, L₂, δ, S₁, S₂, S_δвзять из примера 1.

Решение. Для ориентировки предварительно определим магнитный поток Ф₀ в цепи, учитывая только магнитное сопротивление воздушного зазора R_возд = δ / (μ₀ S_δ) и пренебрегая сопротивлением ферромагнитных участков цепи:

.

Поскольку магнитное сопротивление всей цепи несколько больше, чем сопротивление воздушного зазора, искомый магнитный поток меньше Ф₀. Зададимся в предварительном расчете значением Ф ≈ 0,8 Ф₀ = 0,015 Вб и определим соответствующую этому потоку намагничивающую силу.

Магнитная индукция на отдельных участках цепи:

B₁ = Ф / S₁ = 0,015 / 0,0225 = 0,67 Тл;
B₂ = Ф / S₂ = 0,015 / 0,015 = 1,0 Тл;
B_возд = Ф / S_δ = 0,015 / 0,015 = 1,0 Тл.

По кривой намагничивания для литой стали (рис. 9.2) находим

H₁ = 310 А/м, H₂ = 700 А/м, H_возд = 8 × 10⁵ А/м.

Намагничивающая сила обмотки

F₁ = H₁ L₁ + H₂ L₂ + H_возд δ = 310 × 0,975 + 700 × 0,82 + 8 × 10⁵ × 0,002 = 2470 АВ.

Далее зададимся еще значениями магнитного потока в 0,014 и 0,012 Вб и проведем аналогичные расчеты. Результаты всех расчетов сведены в табл. 9.1.

По данным табл. 9.1 построен график Ф(F) (рис. 9.3). Из графика находим, что заданной намагничивающей силе F = 2000 АВ соответствует магнитный поток Ф = 0,013 Вб.

Таблица 9.1

Ф, Вб	В1, Тл	В2, Тл	Ввозд, Тл	Н1, А/м	Н2, А/м	Нвозд, А/м	Н1 L1, А	Н2 L2, А	Hвоздδ, А	∑HL = F, А
0,015	0,67	1,0	1,0			8×105
0,014	0,62	0,93	0,93			7,4×105
0,012	0,53	0,8	0,8			6,4×105

Рис. 9.3. График Ф(F) (к примеру 2)

Пример 3

Определить число витков и ток в обмотке дросселя (рис. 9.4), сердечник которого изготовлен из листовой электротехнической стали Э 41. Активным сопротивлением обмотки и потоком рассеяния пренебречь. Напряжение источника U = 230 В, частота тока f = 50 Гц, амплитуда магнитной индукции B_m = 1,4 Тл. Размеры сердечника: L₁ = 14 см; L₂ = 10 см; b₁ = 2 см; толщина сердечника b₂ = 3 см. Удельный вес стали γ = 7,8 г/см³. Стальные листы разделены изоляцией, занимающей 10 % всего объема.

Определить ток в обмотке, если в сердечнике выпилить зазор толщиной δ = 1 мм.

Рис. 9.4

Решение. Уравнение электрического равновесия для обмотки дросселя имеет вид:

,

где R₁ – активное сопротивление обмотки;
X₁ – индуктивное сопротивление обмотки, обусловленное потоком рассеяния;
E = 4,44 W f Ф_m – противо-ЭДС, наводимая в обмотке основным магнитным потоком;
Ф_m – амплитуда основного магнитного потока.

Согласно условию задачи R₁ ≈ 0, X₁ ≈ 0 из уравнения равновесия получаем

U = E = 4,44 W f Ф_m,

Ф_m = B_m S_ст = 0,9 B_m S,

где S_ст – площадь поперечного сечения стали;
S – площадь поперечного сечения магнитопровода, включая изоляцию между листами: S = b₁ b₂ = 2 × 10^-2 × 3 × 10^-2 = 6 × 10^-4, м².

Число витков обмотки

.

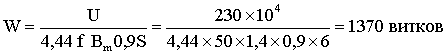Рассмотрим ток в обмотке в виде двух составляющих: активной I_a, определяемой по мощности потерь в стали, и реактивной I_p (намагничивающий ток), зависящей от магнитный свойств цепи и определяемой по закону полного тока, тогда

.

Активная составляющая тока

I_а = P_ст / U, P_ст = p_ст G,

где Р_ст – мощность потерь в стали
p_ст – удельная мощность потерь в стали (таблица 10.1);
G – вес стали.

Найдем вес стальной части (без изоляции) магнитопровода

G = γ S_ст L_ст = 0,9 γ S_ст.

Длина средней силовой линии

L_ст = 2 (L₁ - b₂) + 2 (L₂ - b₁) = 2 (12 + 8) = 40 см.

Вес стали G = 7,8 × 0,9 × 6 × 40 = 1,68 кг.

Удельная мощность потерь в стали определяется соотношением

p_ст = P B_m² / 50,

в котором P / 50 = 1,35 Вт (кг×Тл²) – удельная мощность потерь для данной марки стали (таблица 10.1) при индукции 1 Тл и частоте 50 Гц.

Тогда p_ст = 1,35 × 1,42 = 2,646 Вт/кг, а мощность потерь в стали P_ст = 2,646 × 1,68 = 4,445 Вт.

Активная составляющая тока

I_a = P_ст / U = 4,445 / 230 = 0,019 A.

Рассматриваемая магнитная цепь является однородной, поэтому на основании закона полного тока найдем амплитудное значение намагничивающего тока

I_рm = H_m L_ст / W.

Максимальное значение напряженности найдем по кривой намагничивания (таблица 10.1) для стали Э 41. При В_m = 1,4 Тл, Н_m = 1300 А/м.

Действующее значение намагничивающего тока

А.

Ток в обмотке

А.

Полученные результаты говорят о том, что в катушке с ферромагнитным сердечником активная составляющая тока невелика и можно принимать I ≈ I_p.

Согласно уравнению электрического равновесия амплитуда магнитного потока Ф_m (или амплитуда магнитной индукции) пропорциональна приложенному напряжению U и не зависит от длины воздушного зазора.

С появлением зазора будет изменяться только реактивная составляющая тока, которую найдем при помощи закона полного тока

I_рm W = H_m L_ст + H_0m δ.

Здесь H_0m δ – составляющая МДС катушки, идущая на создание магнитного поля в воздушном зазоре

H_0m = B_m / μ₀ = 1,4 / (4 π 10^-7) = 11,146 × 10⁵ А/м.
I_рm W = 1300 × 0,4 + 11,146 × 10⁵ × 0,001 = 1634,6 АВ.

Таким образом, на создание магнитного поля в небольшом воздушном зазоре тратится большая част МДС. Действующее значение реактивной составляющей тока

А.

Общий ток I ≈ I_p = 0,846 А.

Создание воздушного зазора длиной 1 мм привело к возрастанию тока в катушке в 3 раза.

Практическое занятие №10.