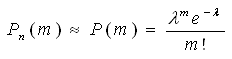Дисперсия случайной величины и ее свойства.
Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.
Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.
Расчетные формулы:
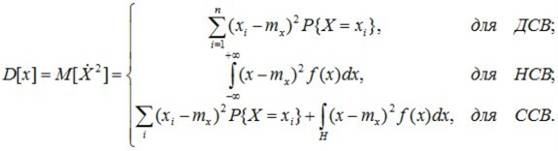(6.9)
Дисперсия может быть вычислена через второй начальный момент:
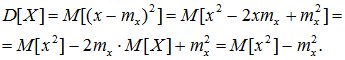(6.10)
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.
Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ.
Средним квадратическим отклонением (СКО) СВ X называется характеристика 
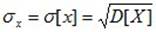. (6.11)
СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ.
Свойства дисперсии
Дисперсия постоянной величины с равна нулю.
Доказательство: по определению дисперсии
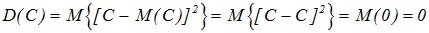
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.
D [ X + c ] = D [ X ].
Доказательство: по определению дисперсии
(6.12)
3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2.
Доказательство: по определению дисперсии
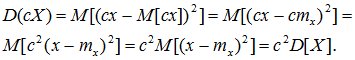. (6.13)
Для среднего квадратичного отклонения это свойство имеет вид:
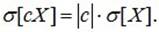(6.14)
Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М [ сХ ] больше, чем возможные значения Х вокруг М [ X ], т.е.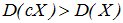 
. Если 0<½с½<1, то 
.
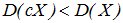Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:
[ m - 3 s; m + 3 s; ].
Биноминальный закон распределения
Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q.
Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:
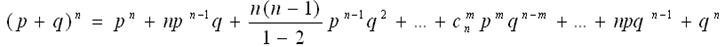
где pn - вероятность того, что при n испытаниях событие А наступит n раз;
qn - вероятность того, что при n испытаниях событие А не наступит ни разу;
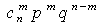- вероятность того, что при n испытаниях событие А наступит m раз, а событие Ā наступит n - m раз;
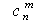- число сочетаний (комбинаций) появления события А и Ā.
Числовые характеристики биноминального распределения:
М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях;
D(m)=npq - дисперсия частоты появления события. А;
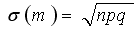- среднее квадратическое отклонение частоты.
Закон Пуассона
Событие называются редкими, когда вероятность события р или противоположного ему q близка к нулю. При большом числе испытаний (n), но небольшой величине произведения числа испытаний на вероятность (np),
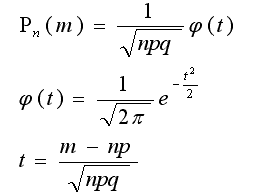
которое меньше 10, вероятности полученные по формуле Лапласа
недостаточно близки к их истинным значениям. тогда применяют другую асимптотическую формулу
Пуассона.
Теорема. Если вероятность р наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, произведение np = λ, то вероятность Рn(m) того, что в n независимых испытаниях события А наступит m раз, приближенно равна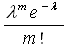 
, т.е.
