ЛАБОРАТОРНАЯ РАБОТА № 4
ИССЛЕДОВАНИЕ ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
Цель работы
Целью работы является изучение свойств и процессов в типовых динамических звеньев САУ. В результате выполнения работы курсант должен знать типовые звенья САУ, их уравнения динамики и передаточные функции, особенности временных и частотных характеристик.
Теоретическая часть
Для теоретического исследования САУ удобно классифицировать их элементы (звенья) не по конструктивным признакам, а по динамическим свойствам, т.е. по их поведению в переходных процессах. Это поведение зависит от вида алгоритма, который связывает их входные и выходные величины. Динамические звенья рассматриваются как удобный «строительный» материал для разработки систем управления, поскольку процессы, протекающие в отдельных звеньях, проще поддаются описанию, чем во всей системе управления.
Особенно удобно для целей исследования разделение САУ на простейшие звенья, описываемые дифференциальными уравнениями не выше второго порядка. Такие звенья называются типовыми звеньями. Все типовые звенья можно разделить на 3 группы в зависимости от поведения их в установившемся режиме:
· позиционные (в установившемся режиме выходная величина прямо пропорциональна входной);
· интегрирующие (выходная величина изменяется в одном направлении до тех пор, пока на входе есть отличный от нуля сигнал),
· дифференцирующие (в установившемся режиме выходной сигнал равен нулю, поскольку выходная величина определяется производной от входного сигнала).
Временные характеристики звеньев описывают реакцию звена на специальные входные воздействия в виде единичной ступенчатой функции и единичного δ-импульса, а частотные характеристики описывают поведение звена в режиме вынужденных установившихся колебаний. Эти функции в такой же степени описывают систему, как и передаточная функция звена  . Каждую из этих характеристик можно экспериментально измерить или рассчитать, зная передаточную функцию звена. Так, в частности, АЧХ, которая показывает как изменяется амплитуда установившихся колебаний, можно вычислить как модуль комплексно-частотной характеристики (КЧХ)
. Каждую из этих характеристик можно экспериментально измерить или рассчитать, зная передаточную функцию звена. Так, в частности, АЧХ, которая показывает как изменяется амплитуда установившихся колебаний, можно вычислить как модуль комплексно-частотной характеристики (КЧХ)  ., а ФЧХ, которая определяет сдвиг фаз входных и выходных колебаний, рассчитывается как аргумент этой функции.
., а ФЧХ, которая определяет сдвиг фаз входных и выходных колебаний, рассчитывается как аргумент этой функции.
Временные характеристики звеньев позволяют рассчитать реакцию звена на произвольное входное воздействие  с помощью интегралов свертки Дюамеля:
с помощью интегралов свертки Дюамеля:
 (4.1)
(4.1)
или же
 (4.2)
(4.2)
В табл. 4.1 приведена классификация динамических звеньев с указаниями выражений для их передаточных функций, а также временных и частотных характеристик.
Табл. 4.1. Типовые звенья и их передаточные функции
| № п/п | Класс Звеньев | Название | Передаточная
функция 
| Характеристики |
| Позиционные | Безынер-ционное | 
|  , ,  , ,
 , ,
| |
| Аперио-дическое 1 порядка | 
|  , , 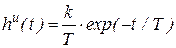 , ,
 , ,
| ||
Аперио-дическое
2 порядка

| 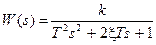
| 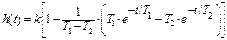 , ,
 , ,
 ,
,
| ||
Коле-
бательное

| 



| |||
Консер-
вативное

| 

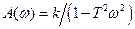

| |||
| Интегрирующие | Идеальное интегри- рующее | 
|  
 , , 
| |
| Интегри-рующее. с замедлением | 
|  , ,
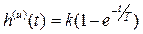 , ,
 , ,

| ||
| Изодром- ное | 
|  , , 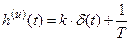
 , ,
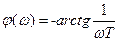
| ||
| Дифф. | Идеальное дифферен-цирующее | 
|  − бесконечно-
высокие и узкие импульсы, − бесконечно-
высокие и узкие импульсы,
 , , 
| |
| Дифферен- цирующее с замед- лением | 
| 

 , ,
 . .
|
Здесь использованы следующие обозначения:
 – коэффициент усиления,
– коэффициент усиления,  – постоянная времени,
– постоянная времени,  – коэффициент демпфирования,
– коэффициент демпфирования,  – время интегрирования (дифференцирования) соответственно, α и β – вещественная и мнимая части корней характеристического уравнения.
– время интегрирования (дифференцирования) соответственно, α и β – вещественная и мнимая части корней характеристического уравнения.
В первой части работы исследуются временные характеристики звеньев. Вначале следует получить переходную и импульсную переходную функции, используя формулы, приведенные в табл. 4.1, и сравнить с результатом вычисления по заданной передаточной функции. Такой расчет по передаточной функции звена удобно выполнять в рамках пакетов компьютерной математики Matlab или Mathcad.
В пакете Matlab расчет временных характеристик следует выполнять c использованием команд приложения CST – step и impulse.
В пакете Mathcad эта задача решается путем формул Солодовникова, которые получены из соотношений обратного преобразования Лапласа:
 (4.3)
(4.3)
 (4.4)
(4.4)
Проиллюстрируем это на примере звена с передаточной функцией  . Перепишем выражение для передаточной функции в виде −
. Перепишем выражение для передаточной функции в виде −  . Следовательно, это апериодическое звено 1 порядка, причем
. Следовательно, это апериодическое звено 1 порядка, причем 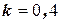 и
и  . Переходная функция его задается выражением
. Переходная функция его задается выражением  , а импульсная переходная – выражением
, а импульсная переходная – выражением 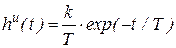 .
.
Пакет Matlab
k=0.4; T=0.6; t=0:0.1:5; s=tf('s'); w=2/(3*s+5);
h1=k*(1-exp(-t/T)); h2=step(w,t); h1i=(k/T)*exp(-t/T);h2i=impulse(w,t);
subplot(1,2,1); plot(t,h1,'-',t(1:5:end),h2(1:5:end),'+'); grid on;
subplot(1,2,2); plot(t,h1i,'-',t(1:5:end),h2i(1:5:end),'+'); grid on;

Рис. 1. Переходная и импульсная переходная функции звена вычисленные различными методами.
Пакет Mathcad

Рис.2. Фрагмент документа Mathcad по расчету временных характеристик звена
Заметим, что верхний предел в интегралах вместо бесконечности можно заменить на достаточно большое число.
Далее следует рассчитать реакцию звена на входной сигнал произвольного вида с использованием формул свертки (4.1) – (4.2), а затем провести проверку расчета используя приложение Simulink. Эти действия также удобно выполнять в рамках одного из пакетов компьютерной математики. В пакете Matlab для вычисления интеграла свертки (4.2) удобно использовать М-файл, текст которого приведен ниже для вышерассмотренного апериодического звена первого порядка и входного воздействия в форме − 
function f=Fy(t,H)
k=0.4; T=0.6;
hi=@(tau,x)(k*exp(-(x-tau)/T)./T);
X=@(tau)exp(-tau).*sin(3*tau);
y=@(tau,x)hi(tau,x).*X(tau);
y1=@(x)quad(@(tau)y(tau,x),0,x);
N=round(t/H);
t1=zeros(1,N); Y=zeros(1,N);
for m=1:N;
t1(m)=H*m;
Y(m)=y1(H*m);
End
plot(t1,Y,'r+'); hold on; grid on;
f=[t1;Y]';
Результаты расчета выходного сигнала в рамках пакета Simulink и методом вычисления интеграла свертки представлены на рис. 3 и рис.4.
 Рис. 3 S-модель определения реакции апериодического звена 1 порядка на произвольный входной сигнал
Рис. 3 S-модель определения реакции апериодического звена 1 порядка на произвольный входной сигнал
|
 Рис.4. Выходная реакция звена апериодического звена второго порядка, вычисленная различными способами
Рис.4. Выходная реакция звена апериодического звена второго порядка, вычисленная различными способами
|
Аналогичные действия можно выполнить в рамках пакета Mathcad. Несложно также выполнить совмещение этого результата расчета с тем, который выполнялся в пакете Simulink.
 Рис.5. Фрагмент документа Mathcad расчета реакции динамического звена на входной сигнал произвольной формы с помощью интеграла свертки
Рис.5. Фрагмент документа Mathcad расчета реакции динамического звена на входной сигнал произвольной формы с помощью интеграла свертки
|
Во второй части работы исследуются частотные характеристики звена. Необходимо двумя различными способами – по известной аналитической формуле и по заданной передаточной функции рассчитать и построить графики ЛАЧХ и ФЧХ. Проиллюстрируем это на примере изучаемого звена в рамках двух пакетов компьютерной математики.
Скрипт команд в Command Window пакета Matlab имеет вид:
>> om=0.001:0.001:10;
>> k=0.4; T=0.6; L1=20*log10(k)-20*log10((1+om.^2.*T.^2).^0.5); fi1=-atan(om*T);
>> w=tf(2,[3 5]); R=freqresp(w,om); R=R(:); A=abs(R); L2=20*log10(A); fi2=angle(R);
>> subplot(1,2,1); semilogx(om,L1,'-',om(1:250:end),L2(1:250:end),'+'); grid on;
>> subplot(1,2,2); semilogx(om,fi1,'-',om(1:200:end),fi2(1:200:end),'+'); grid on;
 Рис.6. Частотные характеристики апериодического звена 1 порядка построенные различными способами
Рис.6. Частотные характеристики апериодического звена 1 порядка построенные различными способами
|
Аналогичные операции в пакете Mathcad представлены ниже.
 Рис.7. Фрагмент документа Mathcad расчета различными способами частотных характеристик динамического звена
Рис.7. Фрагмент документа Mathcad расчета различными способами частотных характеристик динамического звена
|
Выполнение работы
Исследуемое звено и вид произвольного входного сигнала выбирается курсантом из табл. 4.2 в соответствии с его номером n в академическом журнале. Необходимо определить какому типовому звену соответствует заданный вариант и определить параметры его передаточной функции.
В первой части работы необходимо рассчитать и построить 2 способами графики временных характеристик, а также реакцию звена на входной сигнал произвольного вида. Указание: формулу (4.2) удобно использовать, если выражение для импульсной переходной функции не содержит δ-функции.
Во второй части работы следует рассчитать и построить 2 способами графики частотных характеристик. Для графика ЛАЧХ следует провести асимптоты и проверить правильность их наклонов.
Таблица 4. 2
| n | W(s) | 
| N | W(s) | 
|

| 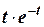
| 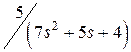
| 
| ||

| 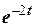
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 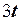
| 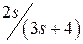
| 
| ||
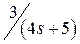
| 
| 
| 
| ||

| 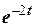
| 
| 
| ||

| 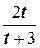
| 
| 
| ||
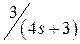
| 
| 
| 
| ||

| 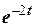
| 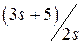
| 
| ||

| 
| 
| 
| ||

| 
| 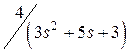
| 
| ||
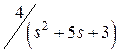
| 
| 
| 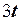
|
4.4. Контрольные вопросы
1. Что называют динамическим звеном? типовым динамическим звеном? С какой целью производят разбиение САУ на звенья?
2. Какова классификация типовых динамических звеньев? Что является основным признаком, по которому звено относят к конкретной группе типовых звеньев?
3. Как аналитически и численно рассчитать переходные характеристики динамических звеньев?
4.. Что называется частотными характеристиками динамического звена? САУ?
5. Каков физический смысл АЧХ и ФЧХ?
6. Как построить амплитудно-фазовую частотную характеристику по известным раздельным характеристикам АЧХ и ФЧХ?
7. Как определить частотные характеристики звена исходя из известного выражения для передаточной функции его?
8. Как экспериментально определить частотные характеристики динамического звена?
9. Как определяются и с какой целью вводятся логарифмические ЧХ?
10. Как рассчитать параметры звена по его логарифмической АЧХ?
ЛАБОРАТОРНАЯ РАБОТА № 5
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САУ
Цель работы
Целью работы является ознакомление с методами исследования устойчивости линейных стационарных непрерывных САУ, а также САУ, содержащих звенья идеального транспортного запаздывания. В результате выполнения работы следует научиться использовать критерии Гурвица и Найквиста для оценки устойчивости и определения критических характеристик звеньев, соответствующего выходу замкнутой системы на границу колебательной устойчивости.
Теоретическая часть
Устойчивость – это свойство системы возвращаться в установившийся режим после исчезновения внешнего воздействия, которое послужило причиной отклонения от этого состояния. Если же внешнее воздействие сохраняет постоянное значение, то система переходит в новое установившееся значение и продолжает оставаться в нем неограниченно долго. В любом случае для устойчивых систем характерно то, что в них, с течением времени, переходное (свободное) движение затухает. Исследование устойчивости является одной из важнейших задач теории автоматики, поскольку работоспособными, очевидно, являются только устойчивые системы.
Системы неустойчивые или нейтральные в разомкнутом состоянии могут приобрести устойчивость при замыкании и, наоборот, системы устойчивые в разомкнутом состоянии могут потерять свою устойчивость при замыкании. Физически это можно пояснить тем, что в замкнутой системе отклонения регулируемого параметра, возникшие в некоторой ее точке, возвращаются в нее же. Тогда, если прохождение через систему не уменьшает величину сигнала (коэффициент усиления контура на частоте сигнала больше единицы), то сигнал будет уже не затухать, а непрерывно увеличиваться – наблюдается эффект самовозбуждения.
В ряде случаев оказывается, что система неустойчива при любых значениях параметров, и сделать ее устойчивой можно только путем изменения структуры. Такого рода системы называются структурно неустойчивыми. Наряду с ними существуют системы, которые устойчивы независимо от значений параметров входящих в них звеньев. Для таких систем порядок характеристического уравнения не выше второго, а коэффициенты уравнения – положительны. Если же порядок системы выше второго, и она составлена из устойчивых (или нейтральных) звеньев (все коэффициенты характеристического уравнения положительны), то при замыкании такая система может потерять устойчивость, а может и сохранить ее. Такие системы называются структурно-устойчивыми и именно они чаще встречаются на практике.
Для них необходимо уметь определять диапазон варьируемых параметров регулятора, которые обеспечивают состояние устойчивости. Так, важной задачей является определение критической величины коэффициента усиления, т.е. такого его наибольшего значения, которое обеспечивает минимальную величину статической ошибки при сохранении состояния устойчивости. Также важным представляется оценка максимальной инерционности регулятора. Именно эти, практически наиболее важные, случаи и исследуется в первой части лабораторной работы.
Для анализа устойчивости линейных систем достаточно исследовать знаменатель передаточной замкнутой системы – ее характеристическое уравнение:
 , (5.1)
, (5.1)
где ai – постоянные коэффициенты.
Необходимым условием устойчивости является требование, чтобы все коэффициенты характеристического уравнения (5.1) имели одинаковый знак, а достаточным условием – чтобы действительные части всех n корней его были отрицательными, т.е. лежали в левой части комплексной плоскости. Если один вещественный корень характеристического уравнения или пара комплексно-сопряженных корней попадает на мнимую ось, то система будет находиться на границе устойчивости.
Поскольку для уравнений порядка выше второго представляет затруднение непосредственное вычисление корней и исследование зависимости их значений от варьируемых параметров системы, то разработаны специальные правила – алгебраические и частотные критерии, позволяющие оценить устойчивость без вычисления корней характеристического уравнения (3.1).
Алгебраические критерии предполагают проверку выполнения системы неравенств, составленных из коэффициентов характеристического уравнения, а частотные критерии являются графоаналитическими, т.е. предусматривают анализ поведения графиков различных частотных характеристик системы. Остановимся на анализе устойчивости с помощью алгебраического критерия Рауса - Гурвица в формулировке Гурвица и в модификации Льенара - Шипара.
Критерий Гурвица предполагает составление из коэффициентов характеристического уравнения матрицы ранга n x n (где n – порядок уравнения) по следующему алгоритму:
· по главной диагонали выписываются все коэффициенты с первого по n -ный;
· каждая последующая верхняя ячейка заполняется элементом, номер которого на единицу больше, а каждая последующая нижняя – элементом, номер которого на единицу меньше;
· если номер коэффициента в ячейке превышает n или меньше, чем 0, то вместо этих элементов в соответствующие ячейки вписываются нули.
Так для систем третьего, четвертого и пятого порядков матрицы Гурвица представляются в виде:

| 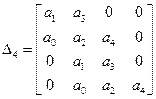
| 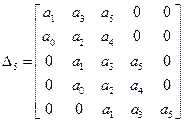
| (5.2) |
Далее по данной матрице составляются диагональные миноры и вычисляются соответствующие значения определителей. Для устойчивости системы все они должны быть положительны. Льенар и Шипар установили, что для проверки устойчивости достаточно установить положительность не всех, а только четных или только нечетных определителей диагональных миноров. Таким образом, для системы 3 порядка достаточно проверить положительность второго минора, для системы 4 порядка – первого и третьего, а для системы 5 порядка второго и четвертого.
Заметим, что последний минор всегда положителен, если положителен предпоследний минор и последний коэффициент при свободном члене, а первый минор также будет положительным, если положителен коэффициент a 1. Поэтому проверка устойчивости (для систем 3 – 5 порядков) сводится к проверке выполнения неравенств[1] представленных в табл. 5.1.
Табл. 5.1. Проверка устойчивости согласно критерию Гурвица.
| Порядок системы | Условие |
| Третий |  (условие Вышнеградского) (условие Вышнеградского)
|
| Четвертый | 
|
| Пятый | 
|
Если система находится на границе устойчивости, то неравенство превращается в равенство, что может быть рассмотрено как уравнение для нахождения критического значения варьируемого параметра.
Во второй части работы исследуются системы с транспортным запаздыванием. Эти системы в одном или нескольких своих звеньях имеют запаздывание во времени изменения выходной величины по отношению к изменению входной на постоянную величину, называемую временем запаздывания.
Звено с запаздыванием обычно можно представить себе в виде последовательно включенных обычного звена без запаздывания и звена «чистого» или идеального транспортного запаздывания (ИТЗ).
Звено с «чистым» запаздыванием описывается уравнением вида:
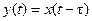 (5.3)
(5.3)
Преобразование Лапласа формулы (5.3) позволяет получить выражение для передаточной функции звена ИТЗ:
W (s)=exp(–t s). (5.4)
Поскольку для этого звена переменная s входит в показатель степени, то характеристическое уравнение замкнутой системы будет трансцендентным (как по каналу возмущения, так и по каналу задающего воздействия). Поэтому для анализа устойчивости таких систем единственно применимым являются частотные графоаналитические критерии, в частности критерий Найквиста.
Этот критерий позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы, т.е. системы, получаемой путем размыкания главной отрицательной обратной связи. Исследуется поведение одновременно двух раздельных частотных характеристик − амплитудной A (ω) и фазовой φ(ω) или же одной объединенной амплитудно-фазовой характеристики (иначе годографа КЧХ). Эти характеристики можно измерить экспериментально или рассчитать теоретически, как это описано ранее.
В соответствии с критерием Найквистадля устойчивости замкнутой системы, составленной из устойчивых (или нейтральных) динамических звеньев годограф КЧХ разомкнутой системы (годограф Найквиста) не должен охватывать критическую точку (-1, j 0) на вещественной оси. Если же годограф проходит через эту точку, то после замыкания система окажется на границе колебательной устойчивости. На рис. 5.1 представлены годографы Найквиста для систем с различным состоянием устойчивости.
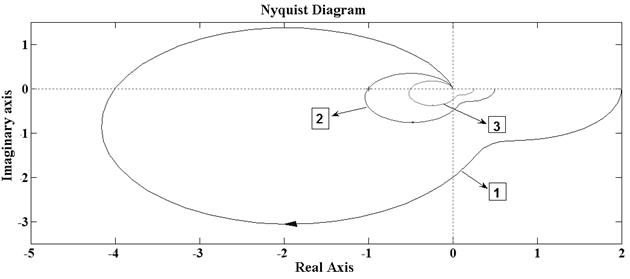 Рис.5.1. Годографы Найквиста для систем с устойчивых в разомкнутом состоянии и различным состоянием устойчивости в замкнутом состоянии. При замыкании система 1 – неустойчива, система 2 – на границе устойчивости, система 3 – устойчива.
Рис.5.1. Годографы Найквиста для систем с устойчивых в разомкнутом состоянии и различным состоянием устойчивости в замкнутом состоянии. При замыкании система 1 – неустойчива, система 2 – на границе устойчивости, система 3 – устойчива.
|
Такое поведение годографа соответствует тому, что логарифмическая амплитудно-частотная характеристика (ЛАЧХ) разомкнутой системы должна раньше пересекать ось абсцисс, чем фазово-частотная характеристика достигает значения –π. Рис. 5.2 иллюстрирует этот факт, представляя набор раздельных частотных характеристик для вышерассмотренных систем. Такие две характеристики называются в совокупности диаграммой Боде.
Критерий Найквиста позволяет ввести важное понятие запаса устойчивости Δφ по фазе. Эта величина определяется тем, насколько фазовый сдвиг в разомкнутой системе отличается от величины –π на частоте среза ω s (частота среза соответствует такому значению частоты, для которого ЛАЧХ разомкнутой системы пересекает ось абсцисс, т.е. A( ω s)=1 или L( ω s)=0). Чем больше величина запаса устойчивости по фазе, тем меньше система чувствительна к возможным вариациям параметров ее звеньев, которые могут привести ее к неустойчивой работе.
 Рис.5.2. Раздельные частотные характеристики для разомкнутых систем с различным состоянием устойчивости. При замыкании система 1 – неустойчива, система 2 – на границе устойчивости, система 3 – устойчива.
Рис.5.2. Раздельные частотные характеристики для разомкнутых систем с различным состоянием устойчивости. При замыкании система 1 – неустойчива, система 2 – на границе устойчивости, система 3 – устойчива.
|
Для анализа устойчивости систем с запаздыванием проанализируем частотные характеристики звена ИТЗ на основе формулы для ее передаточной функции (5.4). Очевидно, что у звена ИТЗ на всех частотах амплитуда передачи сигнала равна единице, а вносимая величина отрицательного фазового сдвига растет с частотой:
 . (5.5)
. (5.5)
Отрицательный фазовый сдвиг в звене ИТЗ негативно сказывается на качестве работы САУ – увеличиваются колебательность и время регулирования (длительность переходного процесса) и уменьшается запас устойчивости системы. При превышении времени запаздывания некоторого критического значения τкр система теряет устойчивость.
Предположим, что до введения звена ИТЗ система обладала запасом устойчивости по фазе Dj, тогда устойчивость замкнутой системы нарушится, если отрицательный фазовый сдвиг (5.5) будет превышать по модулю величину Dj. Условие нахождения системы на границе колебательной устойчивости соответствует выполнению соотношения:
 .
.
Откуда выражение для критического времени транспортного запаздывания:
 . (5.5)
. (5.5)
В ряде простейших случаев величины запаса устойчивости и частоты среза могут быть выражены аналитически через параметры передаточных функций составляющих систему звеньев, однако, в общем случае, значительно удобнее представляется запасы устойчивости с помощью команды CST margin. Листинг использования ее имеет вид:
[Gm Pm om]=margin(w)
где w – передаточная функция разомкнутой системы.
Выполнение работы
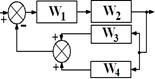
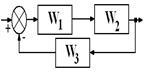
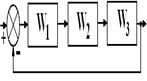
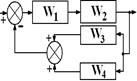
В соответствии со своим номером n в академическом журнале курсант должен из табл. 5.2 выбрать вариант задания, в котором указан вид структурной схемы задачи и заданы значения передаточных функций звеньев.
Таблица 5.2. – Структурная схема САУ и передаточные функции звеньев
| n | Структурная схема | Передаточные функции | n | Структурная схема | Передаточные функции |

| 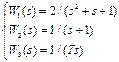
| 
| 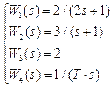
| ||

| 
| 
| 
| ||

| 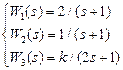
| 
| 
| ||

| 
| 
| 
| ||
| Продолжение таблицы 6.2 | |||||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 
| ||

| 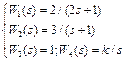
| 
| 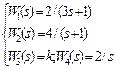
| ||

| 
| 
| 
| ||

| 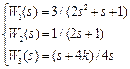
| 
| 
| ||

| 
| 
| 
| ||

| 
| 
| 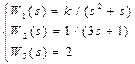
|
[1] Это, конечно, значительно более простая процедура сравнительно с поиском корней.