Лабораторная работа № 4
по дисциплине «Статистика»
на тему «Анализ множественной корреляционной зависимости»
Выполнил: студент группы 33707/1
________________ Егорова Е. В.
Принял:
_______________ Н.В. Куприенко
Оценка: __________________
«___» ___________ 2015 года
Санкт-Петербург
Егорова Е. В. Анализ множественной корреляционной зависимости. Расчетное задание №4 по дисциплине «Статистика». СПб.: СПбГПУ, 2015, стр 12.
СТАТИСТИКА, МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ, КОЛЛИНЕАРНЫЙ ФАКТОР, КОРРЕЛЯЦИОННАЯ МАТРИЦА, ОСТАТОЧНАЯ ДИСПЕРСИЯ, КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ
В лабораторной работе №4 построена корреляционная матрица, проведены необходимые расчеты и сделаны выводы.
СОДЕРЖАНИЕ
1. Построение уравнения множественной регрессии и расчет показателей множественной корреляции 4
1.1. Построение корреляционной матрицы.. 4
1.2. Пошаговый корреляционно-регрессионный анализ. 8
Построение уравнения множественной регрессии и расчет показателей множественной корреляции
Изучение множественной корреляционной зависимости предполагает оценку влияния двух и более факторов на интересующий исследователя признак-результат.
Начнем анализ с построения уравнения регрессии, включив в него все имеющиеся факторы.
Решение с помощью ППП STATISTICA, используя метод наименьших квадратов.
Рис. 1.1. Основные показатели модели множественной регрессии
Рис. 1.2. Таблица параметров уравнения множественной регрессии и их оценок
Построение корреляционной матрицы
Следующим этапом анализа будет построение корреляционной матрицы с целью обоснованного отбора факторов для включения в уравнение: выявления факторов, которые незначительно влияют на результат, а также коллинеарных факторов. (См. рис. 1.3.)
|
|
В полученной матрице содержатся парные коэффициенты корреляции, которые выражают тесноту связи между каждым из факторов и результатом и тесноту связи между факторами. Система помогает пользователю, выделяя красным цветом значения в тех клетках, где пересекаются элементы, связь между которыми значима. В каждой клетке расположены два числа: верхнее – коэффициент корреляции, нижнее – уровень значимости.
Рис.1.3. Корреляционная матрица
Далее необходимо рассмотреть корреляционную матрицу на предмет обнаружения коллинеарных факторов, то есть тех, между которыми существует тесная линейная зависимость. Такими факторами являются x2 и x6, поскольку коэффициент парной корреляции между ними близок к единице. Это означает, что данные факторы опосредуют влияние друг друга, и в модели достаточно оставить лишь один из них.
В уравнение включается тот фактор, у которого коэффициент корреляции с результатом выше (в данном случае – фактор х6).
Строим новое уравнение с отобранными факторами.
Рис. 1.4. Основные показатели модели множественной регрессии с отобранными факторами
Рис. 1.5. Таблица параметров уравнения множественной регрессии с отобранными факторами
+ 
-множественный коэффициент детерминации, убрали коллинеарный фактор. незначительно меньше 
, значит, обоснованно удалили фактор.
После исключения коллинеарности переходим к анализу парных коэффициентов корреляции между результатом и всеми факторами. Находится фактор с наименьшим коэффициентом корреляции и исключается, далее рассчитывается новое уравнение множественной регрессии. Удаление факторов проводится до тех пор, пока выполняется условие 
.
|
|
Следующим шагом удаляем из модели фактор х3.
Рис. 1.6. Основные показатели модели множественной регрессии с отобранными факторами
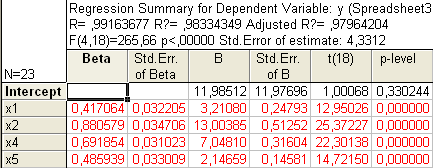
Рис. 1.7. Таблица параметров уравнения множественной регрессии с отобранными факторами
несущественно меньше , значит, убрали незначительный фактор.
Следующим шагом удаляем из модели фактор х1. Строим новое уравнение с отобранными факторами.
Рис. 1.8. Основные показатели модели множественной регрессии с отобранными факторами
Рис. 1.9. Таблица параметров уравнения множественной регрессии с отобранными факторами
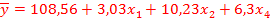
Как мы видим из полученных результатов, после удаления фактора х 1, 
, следовательно фактор х 1 необходимо оставить в модели.
Таким образом, получаем многофакторную модель с изменившимся относительно начального уровня коэффициентом детерминации и отсутствием незначимых параметров. Уравнение в целом также статистически значимо.
k –число коэффициентов модели;
Рис.1.10. Результаты дисперсионного анализа
Расчет остаточной дисперсии в ручную
Рис. 1.11. Расчет остаточной дисперсии в Excel.