ОСНОВЫКРИПТОГРАФИЧЕСКОЙ ЗАЩИТЫИНФОРМАЦИИ
Лабораторная работа №4
Исследование криптосистем, которые используют преобразования в группе точек эллиптической кривой
Цель работы: Изучить и проанализировать свойства примитивов, использующихся при построении криптосистем на основе преобразований в группе точек эллиптической кривой, реализовать аналоги классических асимметричных криптосистем на основе арифметики точек эллиптических кривых.
Задание:
1) Реализовать примитивы для преобразований в группах точек эллиптических кривых с использованием языка программирования высокого уровня.
2) В соответствии с вариантом с помощью примитивов реализовать заданный алгоритм путем замены операции возведения в степень композицией. При реализации использовать навыки, полученные в предыдущей лабораторной работе.
3) Проанализировать вычислительную сложность и криптографическую стойкость вышереализованных систем при их реализации в базовой группе точек и в группе точек эллиптической кривой. Сделать выводы.
| Алгоритм | Бригада |
| Шифр RSA | 1,5 |
| Шифр Эль-Гамаля | 2,6 |
| Шифр Шамира | 3,7 |
| Схема Диффи-Хеллмена | 4,7 |
Теория:
Эллиптической называют кривую 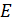 – которая описывается уравнением
– которая описывается уравнением
 ,
,
где  ,
, 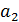 ,
, 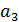 ,
, 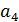 ,
, 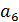
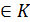 (все действия производятся над полем
(все действия производятся над полем 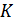 ).
).
Это так называемое уравнение Вейерштрасса.
Для обозначения того, что выбор параметров ЭК и вычисления производятся над определенным полем 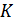 , пользуются нотацией
, пользуются нотацией 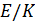 , а само поле называется основным.
, а само поле называется основным.
Быстрое вычисление дискриминанта  можно произвести следующим образом:
можно произвести следующим образом:
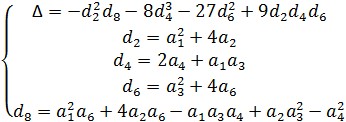
Обычно пользуются эллиптическими кривыми частного вида:
 , ☺
, ☺
Поскольку 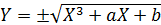 , график кривой симметричен относительно оси абсцисс. Чтобы найти точки его пересечения с осью абсцисс, необходимо решить кубическое уравнение
, график кривой симметричен относительно оси абсцисс. Чтобы найти точки его пересечения с осью абсцисс, необходимо решить кубическое уравнение 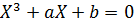 . (☺)
. (☺)
|
|
Дискриминант этого уравнения 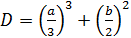 .
.
Сложение точек Удвоение точки
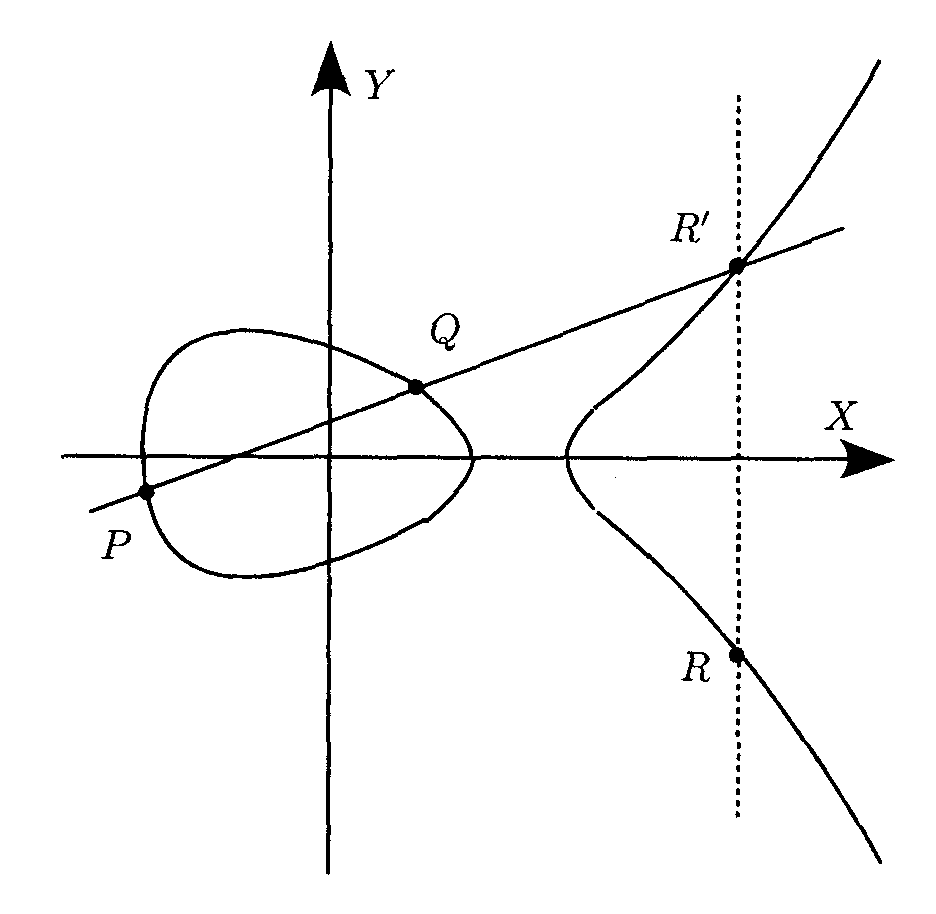
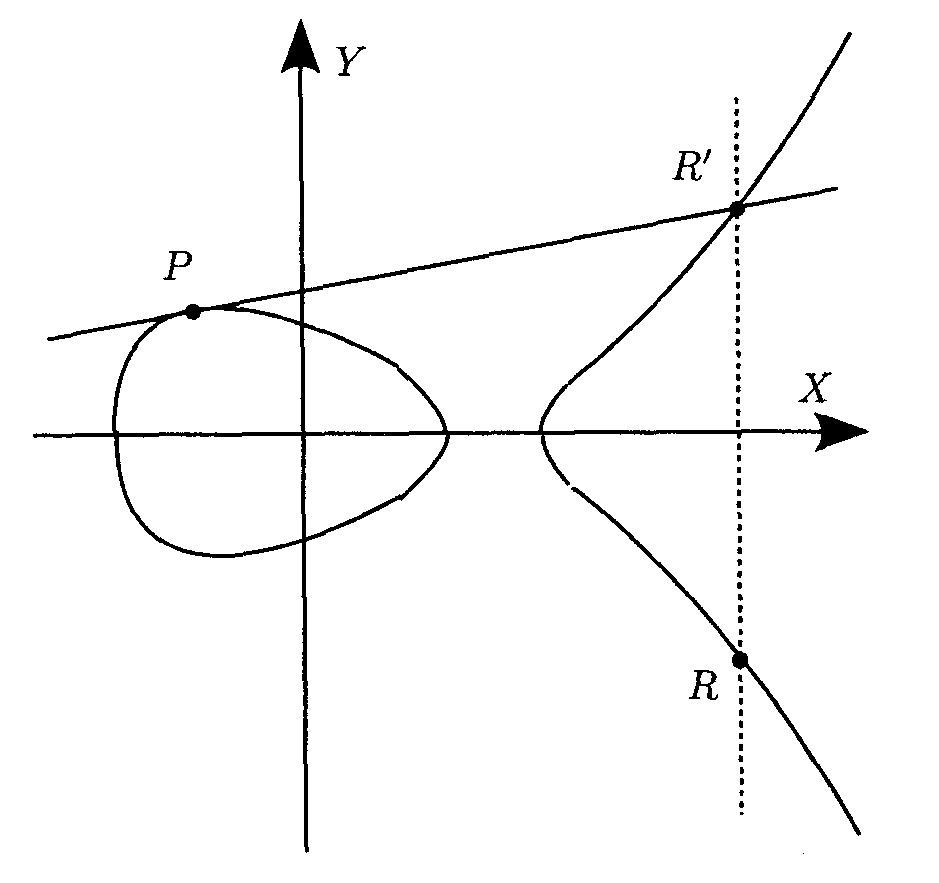
Арифметика группы точек ЭК
1) 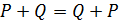 для всех точек
для всех точек 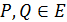 ;
;
2) 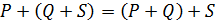 для всех точек
для всех точек  ;
;
3) существует нулевой элемент 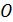 (точка в бесконечности), такой, что
(точка в бесконечности), такой, что 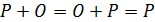 для всех
для всех  ;
;
4) для каждой точки  существует точка
существует точка 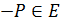 , такая, что
, такая, что 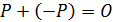 .
.
Корректный выбор эллиптической кривой
Если 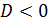 , то (☺) имеет три различных действительных корня
, то (☺) имеет три различных действительных корня 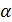 ,
,  ,
, 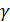 ; если
; если 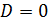 , то (☺) имеет три действительных корня, скажем,
, то (☺) имеет три действительных корня, скажем, 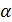 ,
,  ,
,  , по крайней мере два из которых равны; наконец, если
, по крайней мере два из которых равны; наконец, если  , уравнение (☺) имеет один действительный корень а и два комплексно сопряженных.
, уравнение (☺) имеет один действительный корень а и два комплексно сопряженных.
Если 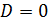 , то кривая является сингулярной, а в точке сингулярности
, то кривая является сингулярной, а в точке сингулярности  имеется две касательные. Для практического использования они непригодны!!! и их необходимо исключать из рассмотрения. Поэтому потребуем, чтобы при выборе параметров ЭК выполнялось соотношение
имеется две касательные. Для практического использования они непригодны!!! и их необходимо исключать из рассмотрения. Поэтому потребуем, чтобы при выборе параметров ЭК выполнялось соотношение


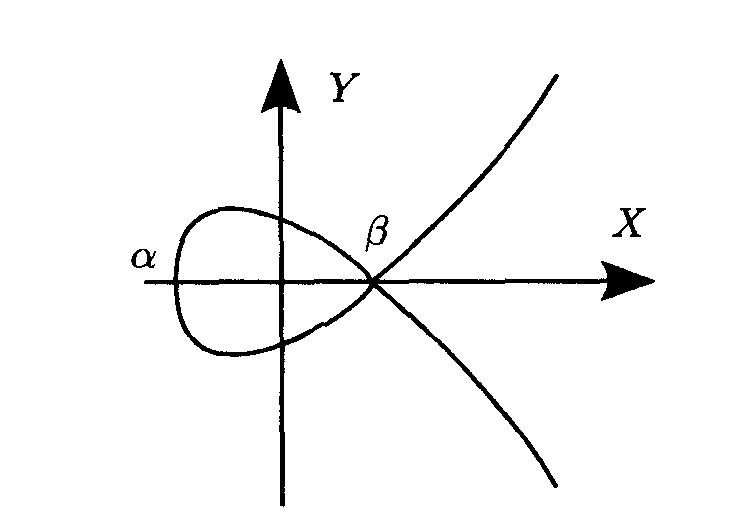
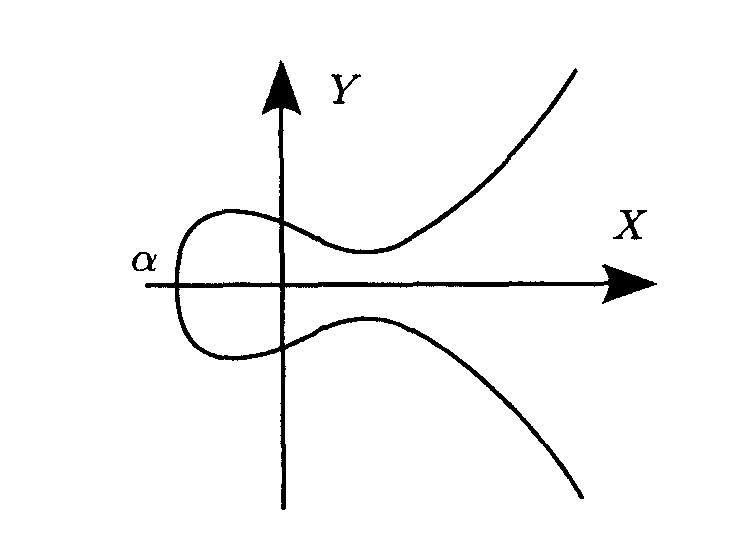
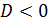
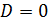

Вид эллиптической кривой для различных значений дискриминанта
Координаты новой точки вычисляются следующим образом:
Для сложения точек:  и
и 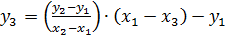 .
.
Для удвоения точки:  и
и  .
.
Основной операцией для эллиптической кривой является - кратная композиция, т.е. вычисление 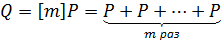
Эта операция выполняется очень эффективно и требует не более 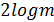 композиций точек. Подходы к ее реализации аналогичны возведению в степень. Например, чтобы получить точку
композиций точек. Подходы к ее реализации аналогичны возведению в степень. Например, чтобы получить точку  , вычисляем
, вычисляем 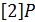 ,
, 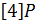 ,
, 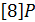 ,
,  , каждый раз удваивая предыдущую точку, и складываем
, каждый раз удваивая предыдущую точку, и складываем 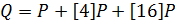 (всего 4 удвоения и 2 сложения).
(всего 4 удвоения и 2 сложения).
Обратная операция, которая по традиции называется дискретным логарифмированием на эллиптической кривой, формулируется следующим образом:
|
|
зная точки 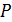 и
и 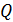 , найти такое число
, найти такое число  , что
, что 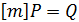 .
.
Эта задача оказывается очень трудной. Если корректно выбирать параметры кривой, то наилучшие в настоящее время алгоритмы для нахождения  требуют
требуют 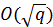 операций на кривой, где
операций на кривой, где  – мощность подмножества точек, которому принадлежат точки
– мощность подмножества точек, которому принадлежат точки 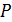 и
и 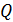 . Все вычисления на кривой проводятся по модулю
. Все вычисления на кривой проводятся по модулю  , т.е. с числами длины
, т.е. с числами длины  бит. Для криптографических приложений
бит. Для криптографических приложений  , поэтому
, поэтому  означает экспоненциальный рост трудоемкости при увеличении длины чисел.
означает экспоненциальный рост трудоемкости при увеличении длины чисел.
Редуцированные кривые
Если базовым полем для эллиптической кривой является конечное поле 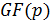 , где
, где  – простое число, то уравнение кривой будет иметь следующий вид:
– простое число, то уравнение кривой будет иметь следующий вид:
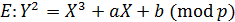
В этом уравнении переменные 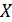 ,
,  и коэффициенты
и коэффициенты 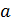 ,
,  принимают целочисленные значения, а все вычисления производятся по модулю
принимают целочисленные значения, а все вычисления производятся по модулю  . В соответствии с этим на использование кривой для построения арифметики налагается ограничение
. В соответствии с этим на использование кривой для построения арифметики налагается ограничение
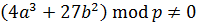 .
.
Именно редуцированные эллиптические кривые, определенные в конечном поле 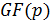 и используются в криптографии.
и используются в криптографии.
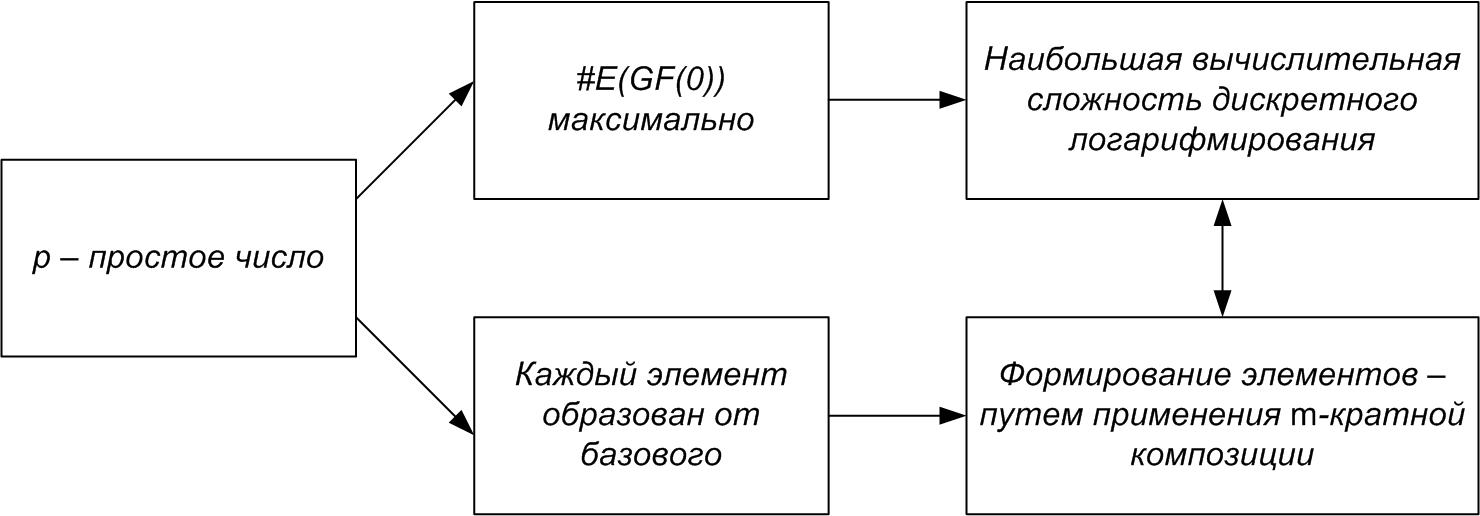
Если  – простое число, то количество элементов в
– простое число, то количество элементов в 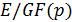 максимально. Если число точек в
максимально. Если число точек в 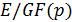 – простое число, то
– простое число, то 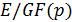 является циклической.
является циклической.
Быстрое вычисление  -кратной композиции
-кратной композиции
ВХОД: Точка  , число
, число 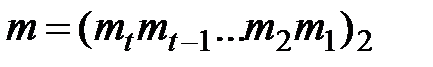 .
.
ВЫХОД: 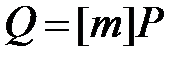 .
.
1. 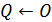 ;
;
2. for 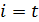 downto 1 do
downto 1 do
3. 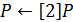 ;
;
4. if  then
then 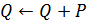 .
.
5. end
6. return 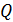 .
.