Гипербола и её каноническое уравнение
Каноническое уравнение гиперболы имеет вид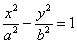 
, где 
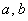– положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие 
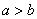, то есть, значение «а» может быть и меньше значения «бэ».
У гиперболы две симметричные ветви.
У гиперболы две асимптоты.
Пример 1
Построить гиперболу, заданную уравнением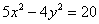 
Решение:
Приводим данное уравнение к каноническому виду .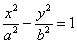
Справа необходимо получить «единицу», поэтому обе части исходного уравнения делим на 20:
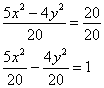
Здесь можно сократить обе дроби
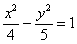
Выделяем квадраты в знаменателях:
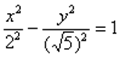
Итак, воспользуемся каноническим уравнением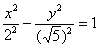 
:
Целесообразно придерживаться следующего алгоритма
1) Прежде всего, находим асимптоты.
Если гипербола задана каноническим уравнением 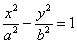, то её асимптотами являются прямые 
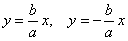. В нашем случае: 
.
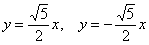Данный пункт обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.
2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках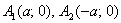 
. Выводится элементарно: если 
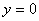, то каноническое уравнение 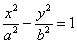превращается в 
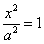, откуда и следует, что 
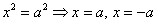. Рассматриваемая гипербола имеет вершины 
3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения 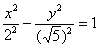на черновике выражаем:
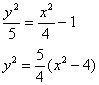
Уравнение распадается на две функции:
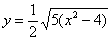– определяет верхние дуги гиперболы (то, что нам надо);
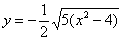– определяет нижние дуги гиперболы.
|
|
Напрашивается нахождение точек с абсциссами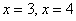 
:
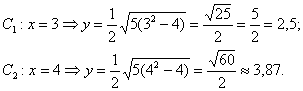
4) Изобразим на чертеже асимптоты 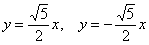, вершины , дополнительные 
и симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
Техническая трудность может возникнуть с иррациональным угловым коэффициентом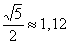 
, но это вполне преодолимая проблема.
Отрезок 
называют действительной осью гиперболы,
его длину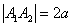 
– расстоянием между вершинами;
число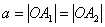 
называют действительной полуосью гиперболы;
число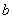 
– мнимой полуосью.
В нашем примере: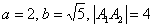 
.
Ф окусы и эксцентриситет
У гиперболы, точно так же, как и у эллипса, есть две особенные точки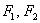 
, которые называются фокусами.
Если гипербола задана каноническим уравнением 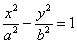, то расстояние от центра симметрии до каждого из фокусов рассчитывается по формуле: 
.
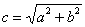И, соответственно, фокусы имеют координаты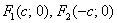 
.
Для исследуемой гиперболы :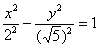
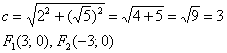
Эксцентриситетом гиперболы называют отношение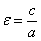 
.
Так как расстояние от центра до фокуса больше расстояния от центра до вершины: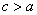 
, то эксцентриситет гиперболы всегда больше «единицы»: 
.
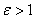Для данного примера: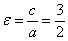 
.
При увеличении эксцентриситета ветви гиперболы «распрямляются» к оси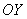 
.
В предельном случае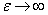 
они стремятся занять положение двух прямых, проходящих через точки 
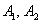параллельно оси ординат.
Если же значение эксцентриситета приближается к единице, то ветви гиперболы «сплющиваются» к оси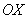 
.
Равносторонняя гипербола
На практике часто встречается гипербола с равными полуосями. Если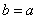 
, то каноническое уравнение 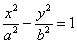заметно упрощается:
|
|
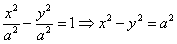
А вместе с ним упрощаются и уравнения асимптот:
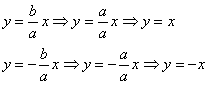
Прямые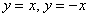 
пересекаются под прямым углом и «справедливо» делят координатную плоскость на 4 одинаковые части, в двух из которых находятся ветви кривой. Образно говоря, равносторонняя гипербола «идеально сложена», то есть и не растянута и не сплющена.
Так как 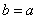, то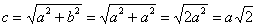 
, следовательно, эксцентриситет любой равносторонней гиперболы равен: 
.
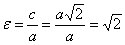Пример 2
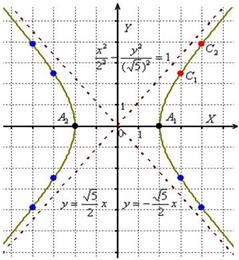
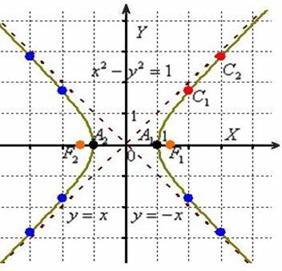
Построить гиперболу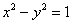 
и найти её фокусы.
Решение: данная гипербола является равносторонней, поэтому имеет асимптоты 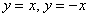. Действительная полуось 
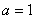, значит, вершины расположены в точках 
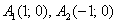. Найдём дополнительные точки:
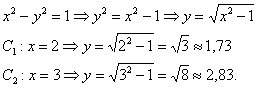
Определим координаты фокусов: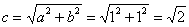 
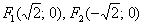
Выполним чертёж.