Свойства скалярного произведения.
Для любых векторов 
и 
справедливы следующие свойства скалярного произведения:
1. свойство коммутативности скалярного произведения 
;
2. свойство дистрибутивности 
или 
;
3. сочетательное свойство 
или 
, где 
- произвольное действительное число;
4. скалярный квадрат вектора всегда не отрицателен 
, причем 
тогда и только тогда, когда вектор 
нулевой.
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения . По определению 
и 
. В силу свойства коммутативности операции умножения действительных чисел, справедливо 
и 
, тогда 
. Следовательно, , что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть, 
и 
, откуда следует
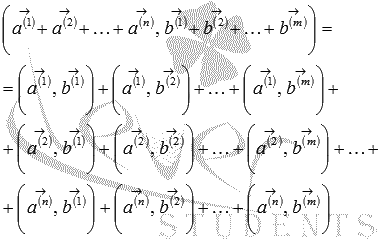
Вычисление скалярного произведения, примеры и решения.
Решение различных задач на вычисление скалярного произведения векторов сводится к использованию свойств скалярного произведения и формул
1. 
;
2. 
;
3. или 
;
4. 
.
Разберем решения наиболее часто встречающихся примеров.
Начнем с самых простых случаев, когда вычисление скалярного произведения производится на основе определения.
Пример.
Вычислите скалярное произведение двух векторов и 
, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.
Решение.
У нас есть все данные, чтобы вычислить скалярное произведение по определению: 
.
|
|
Ответ:
.
Пример.
В прямоугольной системе координат заданы два вектора 
и 
, найдите их скалярное произведение.
Решение.
В этом примере целесообразно использовать формулу, позволяющую вычислить скалярное произведение векторов через их координаты:
Ответ:
.
Пример.
Вычислите скалярное произведение векторов 
и 
, если известны координаты трех точек в прямоугольной декартовой системе координат на плоскости 
.
Решение.
Найдем координаты векторов по координатам точек их начала и конца:
Теперь можно использовать формулу для вычисления скалярного произведения в координатах:
Ответ:
.
Сейчас рассмотрим пример, требующий сначала применить свойства скалярного произведения, и только затем переходить к вычислению.
Пример.
Вычислите скалярное произведение векторов 
и 
, если векторы 
и 
перпендикулярны и их длины равны 3 и 2 единицы соответственно.
Решение.
. По свойству дистрибутивности скалярного произведения имеем 
. Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
.
Итак, после применения свойств скалярного произведения имеем 
. Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ:
.
Сейчас рассмотрим пример на нахождение скалярного произведения векторов через числовую проекцию.
Пример.
Вычислите скалярное произведение векторов и , если 
, а проекция вектора на направление вектора имеет координаты 
.
Решение.
Векторы и 
противоположно направленные, так как 
, следовательно, числовая проекция вектора на направление вектора будет равна длине вектора 
со знаком минус: 
.
|
|
Вычисляем скалярное произведение 
.
Ответ:
.
Также встречается масса обратных задач, когда скалярное произведение векторов известно, а требуется найти, например, длину одного из векторов, угол между векторами, числовую проекцию, либо что-нибудь еще.
Пример.
При каком значении скалярное произведение векторов 
и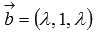 
равно -1.
Решение.
Так как скалярное произведение равно сумме произведений соответствующих координат, то 
. С другой стороны по условию 
. Тогда искомое значение находим из уравнения 
, откуда 
.
Ответ:
.