Лекции 6-7 Системы линейных уравнений (СЛУ)
Содержание лекций: Системы линейных уравнений, основные понятия и определения. «Квадратные» системы, решение «квадратных» систем: 1) с помощью обратной матрицы; 2) по правилу Крамера. Методы исследования и решения произвольных систем. Ранг матрицы, свойства ранга, его вычисление. Однородные системы линейных уравнений.
Основные определения и понятия
Совокупность уравнений вида
 (1),
(1),
называется системой т линейных уравнений с п неизвестными. Здесь аij – коэффициенты при неизвестных, хi – неизвестные, bj – свободные члены системы (i = 1,2,…, n, j = 1,2,…, m).
Если из коэффициентов системы составить матрицы:
 – основную матрицу системы,
– основную матрицу системы,
Х= 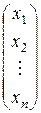 – матрицу-столбец неизвестных,
– матрицу-столбец неизвестных,
В =  – матрицу-столбец свободных членов,
– матрицу-столбец свободных членов,
то система (1) может быть записана в виде равносильного ей матричного уравненияАХ = В.
Наряду с перечисленными матрицами для СЛУ (1) рассматривают матрицу
 ,
,
которую называют расширенной матрицей системы.
Определение 1.
Решением системы (1) называется упорядоченная совокупность п действительных чисел a1, a2,..., a п, при подстановке которых в систему вместо х 1, х 2,…, хn соответственно, каждое уравнение этой системы обращается в верное равенство.
Система называется совместной, если она имеет хотя бы одно решение, в противном случае система несовместна.
Если система линейных уравнений имеет единственное решение, то её называют определённой, если совместная система имеет более одного решения, то её называют неопределённой.
Исследовать систему – значит, выяснить
1) является ли эта система совместной?
2) если система совместна, сколько решений она имеет (т.е. определенная система или неопределенная)?
Решить систему – значит, исследовать ее и в случае совместности найти все решения этой системы.
С помощью перечисленных выше матриц можно исследовать и решать заданную СЛУ.
Рассмотрим частные виды СЛУ.
Решение «квадратных» СЛУ.
Пусть т = п, т.е. число уравнений системы равно числу ее неизвестных
 (2)
(2)
В этом случае основная матрица системы (2) есть квадратная матрица, поэтому такие системы также называют «квадратными». Рассмотрим методы исследования и решения таких систем.
I. Матричный метод.
Как уже отмечалось, с помощью матриц
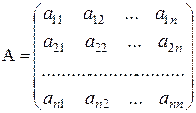 ,
, 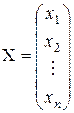 ,
,  ,
,
система (2) может быть записана в виде матричного уравнения АХ = В. Если матрица А невырожденная, то для нее существует обратная матрица А–1. Умножая обе части равенства АХ = В на А–1 слева, получим
(А–1А)Х = А–1В Þ ЕХ = А–1В Þ Х = А–1В.
Эта формула и выражает суть матричного метода решения «квадратной» системы.
Таким образом, если основная матрица «квадратной» СЛУ невырожденная, то система совместна и, чтобы найти решение этой системы, достаточно обратную матрицу для основной матрицы системы умножить слева на столбец свободных членов. При этом, т.к. обратная матрица для заданной единственна, то СЛУ имеет единственное решение.
Пример
Найти решение системы линейных уравнений

с помощью обратной матрицы.
Решение. Рассмотрим основную матрицу системы

и вычислим её определитель:
 .
.
Так как  , то заданная система совместна и имеет единственное решение, а матрица А имеет обратную матрицу
, то заданная система совместна и имеет единственное решение, а матрица А имеет обратную матрицу  . Решение системы найдем по формуле
. Решение системы найдем по формуле
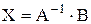 ,
,
где Х=  - матрица-столбец неизвестных, В=
- матрица-столбец неизвестных, В=  – матрица-столбец свободных членов данной системы. Матрица
– матрица-столбец свободных членов данной системы. Матрица  для матрицы А была найдена в примере 1.6:
для матрицы А была найдена в примере 1.6:
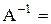
 .
.
Тогда решение данной системы имеет вид
Х= 
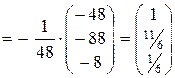 .
.
Отсюда  .
.
Проверка: 
Таким образом, тройка чисел  является решением заданной системы.
является решением заданной системы.
Заметим, что если основная матрица СЛУ вырожденная, то вопрос о совместности системы остается открытым, но матричный метод применять уже нельзя.
II. Правило Крамера.
В основе метода лежит теорема:
Теорема (Крамера)
Если в «квадратной» СЛУ определитель |A| основной матрицы системы отличен от нуля, то система имеет единственное решение и неизвестные хi могут быть найдены по формулам
 , (3)
, (3)
где D = |A| ¹ 0 – определитель основной матрицы системы, а D i - определитель, получаемый из определителя D заменой его i -го столбца столбцом свободных членов.
Определитель D = |A| называют главным определителем системы, определители D i – побочными.
Доказательство: Так как D = |A| ¹ 0, то Х = А–1В, откуда получаем
Х= 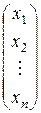 =
=  .
.  =
=
= 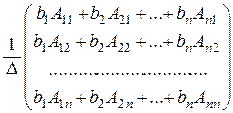 , откуда
, откуда  .
.
Рассмотрим определитель

Если в этом определителе заменить i -й столбец столбцом свободных членов, то получим определитель

Следовательно,  =
=  . ЧТД.
. ЧТД.
Замечание. Формулы  дают возможность исследовать совместность СЛУ:
дают возможность исследовать совместность СЛУ:
Если D ¹ 0, то система совместна и определенна.
Если D = 0, но хотя бы один D i ¹ 0, то система несовместна.
Если D = 0 и все D i = 0, то система может быть совместной, но неопределенной, а может быть и несовместной.
Пример
Доказать совместность системы линейных уравнений

и решить её методом Крамера.
Решение. Чтобы проверить, совместна ли система, рассмотрим основную матрицу системы
А= 
и найдем её определить
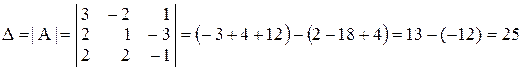 .
.
Так как  , то данная система совместна и имеет единственное решение. Найдем это решение по формулам Крамера
, то данная система совместна и имеет единственное решение. Найдем это решение по формулам Крамера
 .
.
Для этого вычислим вспомогательные определители  ,
, 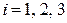 .
.
Определитель D1 получим из определителя D заменой первого столбца  столбцом свободных членов
столбцом свободных членов 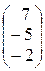 :
:
 = (– 7–10 –12) – (–2 – 42 –10) = –29 + 54 = 25.
= (– 7–10 –12) – (–2 – 42 –10) = –29 + 54 = 25.
Определитель D2 получим из определителя D заменой второго столбца столбцом свободных членов:
 .
.
И, наконец, определитель D3 получим из определителя D заменой второго столбца столбцом свободных членов:
 .
.
Тогда получим искомое решение
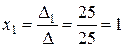 ,
,  ,
,  .
.
Сделаем проверку:

Таким образом, найденная тройка чисел (1; –1; 2) удовлетворяет всем уравнениям заданной системы линейных уравнений и, следовательно, является решением этой системы.