Рассмотрим произвольную матрицу
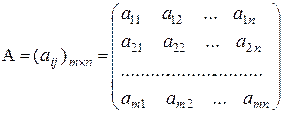
Выберем любые k строк и k столбцов этой матрицы (k £ min(m, n)) и из элементов, стоящих на пересечении выбранных строк и столбцов, составим определитель. Этот определитель называют минором k -го порядка матрицы А.
Например, для матрицы
А = 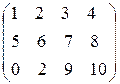
минорами второго порядка, например, являются определители:  ,
,  , а один из миноров третьего порядка имеет вид
, а один из миноров третьего порядка имеет вид 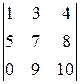 .
.
Определение 3
Наивысший порядок отличных от нуля миноров матрицы А называется рангом этой матрицы.
Ранг матрицы А обозначается rang A или r (A).
Ранг матрицы обладает свойствами:
· для матрицы А = (аij) m ´ n 0£ r (A) £ min(m, n), причем r (A) = 0 тогда и только тогда, когда А – нулевая матрица;
· для квадратной матрицы А порядка п r (A) = п тогда и только тогда, когда А – невырожденная;
· r (A) = r (Aт);
· ранг матрицы не изменится, если вычеркнуть из нее или приписать к ней нулевой ряд (т.е. строку или столбец, состоящие из одних нулей);
· ранг матрицы АЭ, полученной из матрицы А с помощью элементарных преобразований, равен рангу исходной матрицы А.
На свойствах ранга базируется следующий принцип вычисления ранга матрицы:
Заданную матрицу А элементарными преобразованиями приводят к виду
 ,
,
где c 11. c 22. c 33..... ckk ¹ 0, k £ m. Такую матрицу называют трапециевидной. Если k = m = п, то матрица АЭ – треугольная.
Так как матрица АЭ имеет отличный от нуля минор k -го порядка
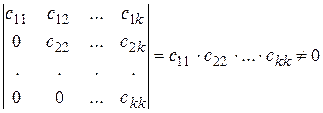
а все миноры более высоких порядков равны нулю (поскольку содержат нулевые строки), то r (АЭ) = k, а значит, и r (A) = r (АЭ) = k. Следовательно, ранг матрицы А равен числу ненулевых строк матрицы АЭ, полученной из матрицы А элементарными преобразованиями.
Справедлива следующая теорема
Теорема (Кронекера-Капелли)
Система линейных уравнений совместна тогда и только тогда, когда ранг r(A) основной матрицы системы равен рангу r( ) расширенной матрицы, т.е.
) расширенной матрицы, т.е.  (без доказательства).
(без доказательства).
Число r = 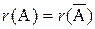 называют рангом системы уравнений.
называют рангом системы уравнений.
Исследование системы с помощью ранга можно проводить следующим образом:
1. Вычислить r (A) и r ( ); если r (A) ¹ r (
); если r (A) ¹ r ( ), то система несовместна;
), то система несовместна;
2. Если r (A) = r (`А) = r, то система совместна и
а) при r = п имеет единственное решение;
б) при r < n имеет бесчисленное множество решений. В этом случае r неизвестных СЛУ являются базисными, остальные  неизвестных – свободными. Базисными неизвестными выбирают те, коэффициенты при которых в матрице АЭ образуют отличный от нуля минор (базисный минор).
неизвестных – свободными. Базисными неизвестными выбирают те, коэффициенты при которых в матрице АЭ образуют отличный от нуля минор (базисный минор).
Рассмотрим пример.
Пример
Исследовать СЛУ 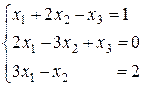 и в случае совместности – решить.
и в случае совместности – решить.
Решение
Запишем расширенную матрицу системы и найдем ее ранг, преобразовав к трапециевидной форме

 `А=
`А= 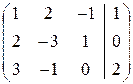 Þ
Þ  Þ
Þ  = =`АЭ.
= =`АЭ.
Ранг матрицы `АЭ равен 3 (три ненулевые строки), а значит и r  =3. Однако матрица, элементы которой стоят слева от вертикальной черты – есть матрица АЭ для основной матрицы системы (которая записана в ` А слева от вертикальной черты). А эта матрица имеет только две ненулевые строки, что означает r (АЭ) = r (А) = 2. Таким образом, r (A) ¹ r
=3. Однако матрица, элементы которой стоят слева от вертикальной черты – есть матрица АЭ для основной матрицы системы (которая записана в ` А слева от вертикальной черты). А эта матрица имеет только две ненулевые строки, что означает r (АЭ) = r (А) = 2. Таким образом, r (A) ¹ r  и в этом случае система несовместна.
и в этом случае система несовместна.
Если же рассмотреть систему  , (изменен свободный член в последнем уравнении предыдущей системы), то нетрудно убедиться в ее совместности:
, (изменен свободный член в последнем уравнении предыдущей системы), то нетрудно убедиться в ее совместности:

 `А=
`А= 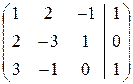 Þ
Þ  Þ
Þ 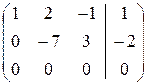 = =`АЭ,
= =`АЭ,
значит, r (A) = r  = r = 2 – система совместна. Число неизвестных п = 3 и r < n, в этом случае система имеет множество решений.
= r = 2 – система совместна. Число неизвестных п = 3 и r < n, в этом случае система имеет множество решений.
Однородные СЛУ
Рассмотрим систему
 .
.
Если хотя бы одно из чисел bi, i = 1,2,…, m не равно нулю, то система называется неоднородной. Если же все bi = 0, то система имеет вид
 (7),
(7),
и называется однородной.
Всякая однородная система совместна, так как имеет, по крайней мере, нулевое (тривиальное) решение х 1 = х 2 = …= хп = 0. Следовательно, ранги основной и расширенной матрицы однородной системы равны:
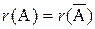 = r.
= r.
Если ранг однородной системы равен числу неизвестных (r = n), то система (7) имеет единственное решение и это решение – тривиальное. Если ранг системы меньше числа неизвестных (r < n), то система имеет бесчисленное множество решений, значит, имеет нетривиальные решения. В этом случае общее решение однородной системы может быть найдено методом Гаусса.
Рассмотрим пример. Дана однородная система линейных уравнений

Требуется:
1) доказать, что система имеет нетривиальное решение;
2) записать общее решение этой системы уравнений и какое-либо нетривиальное частное решение.
Найдем сначала ранг системы (ранг основной матрицы), для чего преобразуем основную матрицу системы:


 .
.
Значит, r (A) = 2. Так как ранг системы меньше числа неизвестных, система имеет нетривиальные решения.
Чтобы найти общее решение системы, составим по полученной матрице систему уравнений, равносильную исходной системе. При этом учитываем тот факт, что в процессе преобразований матрицы мы поменяли местами второй и третий её столбцы, значит, в составляемой системе поменяются местами неизвестные х 2 и х 3:
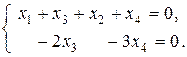 .
.
Коэффициенты при неизвестных х 1 и х 3 образуют отличный от нуля определитель:  , значит эти неизвестные можно взять в качестве базисных, тогда неизвестные х 2 и х 4 – свободные. Перепишем последнюю систему в виде
, значит эти неизвестные можно взять в качестве базисных, тогда неизвестные х 2 и х 4 – свободные. Перепишем последнюю систему в виде
 (8)
(8)
Чтобы записать общее решение системы, положим х 2 = с 1, х 4 = с 2, где с 1, с 2 – произвольные действительные числа. Получим
 .
.
Тогда общее решение однородной системы запишется в виде
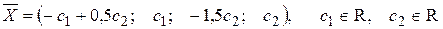
где с 1 и с 2 - произвольные действительные числа.
Найдем какое-либо нетривиальное частное решение системы. Для этого придадим, постоянным  произвольные значения, не равные одновременно нулю. Например, положим
произвольные значения, не равные одновременно нулю. Например, положим 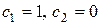 , получим
, получим
 .
.