Раздел 2. Статистические методы распознавания состояний. Методы оценки информативности диагностических признаков

ПК – 17 [2.1.1]

ВЫБОР

Метод определения технического состояния объекта диагностирования, позволяющий отнести с некоторой вероятностью текущее состояние объекта диагностики к одному из заранее установленных классов, – это …

– логический метод

– метод статистической классификации

– вероятностный метод

– детерминистский метод.

 

ПК – 17 [2.1.1]

ВЫБОР

Метод распознавания состояния, использующий сравнение полученного набора значений диагностических признаков с заранее установленными их наборами в различных состояниях, называется …

– методом трафаретов

– методом Байеса

– методом классификации

– методом последовательного анализа

 

ПК – 17 [2.1.1]

ВЫБОР

Метод определения условных вероятностей заданного набора состояний объекта, использующий вероятности состояний и вероятности появления признаков в этих состояниях – это …

– метод сравнения

– метод классификации

– метод последовательного анализа

– метод Байеса

 

ПК – 17 [2.1.1]

ВЫБОР

Вероятность P(A˄k) совмещения двух событий: нахождения объекта в состоянии A и наличия в этом состоянии признака k определится как: …

– P(A˄k) = P(A)·P(A/k)

– P(A˄k) = P(A)/P(A/k)

– P(A˄k) = P(A/k)/P(A)

– P(A˄k) = P(A)·P(k/A)

ПК – 17 [2.1.1]

ВЫБОР

Условная вероятность P(A/k) диагноза состояния A, устанавливаемая по наличию в этом состоянии одного признака k в соответствии с формулой Байеса, определится как: …

– P(A/k) = P(A)·P(k/A)/P(k)

– P(A/k) = P(A)·P(k/A)/P(A/k)

– P(A/k) = P(k)·P(k/A)/P(A)

– P(A/k) = P(A)·P(k/A)

 

ПК – 17 [2.1.1]

ВЫБОР

Условная вероятность P(k/A) появления признака k в состоянии объекта A в соответствии с формулой Байеса, определится как: …

– P(k/A) = P(A)·P(k/A)/P(A/k)

– P(k/A) = P(k)·P(A/k)/P(A)

– P(A/k) = P(k)·P(k/A)/P(A)

– P(A/k) = P(A)/P(k/A)

 

ПК – 17 [2.1.1]

ВЫБОР

Условная вероятность P(K/A) появления комплекса K независимых признаков в состоянии A объекта, если известны условные вероятности появления отдельных признаков k₁, k₂,…, k_n, определится как: …

– P(K/A) = P(k₁)·P(k₂) ·…·P(k_n)

– P(K/A) = P(k₁/A)/P(k₂/A) /…/P(k_n/A)

– P(K/A) = P(k₁/A)·P(k₂/A) ·…·P(k_n/A)

– P(K/A) = P(A/k₁)·P(A/k₂) ·…·P(A/k_n)

 

ПК – 17 [2.1.1]

ВЫБОР

Условная вероятность P(A/K) диагноза состояния A, устанавливаемая по наличию в этом состоянии комплекса K признаков в соответствии с обобщенной формулой Байеса, определится как: …

– P(A/K) = P(A)·P(K/A)/P(A/K)

– P(A/K) = P(K)·P(KA)/P(A)

– P(A/K) = P(A)·P(K/A)

– P(A/K) = P(A)·P(K/A)/P(K)

 

ПК – 17 [2.1.2]

ВЫБОР

Таблица, в которой приводятся апостериорные условные вероятности наличия или отсутствия признаков в различных состояниях и безусловные вероятности этих состояний – это …

– диагностическая матрица

– таблица состояний и проверок

– таблица сравнения состояний

– таблица диагнозов

 

ПК – 17 [2.1.2]

ВЫБОР

Таблица, пример которой показан на рисунке, – это …

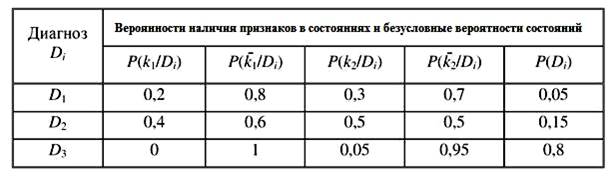
– таблица состояний и проверок

– диагностическая матрица

– таблица сравнения состояний

– таблица диагнозов

 

ПК – 17 [2.1.3]

ВЫБОР

Выбор диагноза состояния объекта с комплексом признаков K по методу Байеса заключается …

– в сравнении вероятностей состояний

– в выборе минимального значения вероятности при появлении признаков

– в сравнении наибольшей вероятности с заданным вероятностным порогом – в выборе диагноза по наибольшей вероятности

 

ПК – 17 [2.1.3]

ВЫБОР

Условие K*Î D_i, если P(D_i/K*) больше или равно пороговой вероятности P_пор, означает, что …

– объект находится в состоянии D_i

– состояние D_i объекта отвергается

– распознавание диагноза невозможно

– объект находится в конкурирующем состоянии

 

ПК – 17 [2.1.3]

ВЫБОР

Условие K*Ï D_i, если P(D_i/K*) меньше пороговой вероятности P_пор, означает, что …

– объект находится в состоянии D_i

– состояние D_i объекта отвергается

– распознавание диагноза невозможно

– объект находится в исправном состоянии

 

ПК – 17 [2.2.1]

ВЫБОР

Принятие решений о продолжении эксплуатации объекта диагностирования или выводе его из эксплуатации принимается с использованием …

– метода Байеса

– теории принятия статистических решений

– метода последовательного анализа

– теории информации

 

ПК – 17 [2.2.1]

ВЫБОР

Выражения ( если k < k₀, то k Î D₁) или ( если k > k₀, то k Î D₂) при зарегистрированномзначении параметра k, пороговом значении k₀ при двух диагнозах D₁ и D₂ означают …

– сравнение диагнозов

– сравнение параметров

– решающее правило

– выбор порогового значения

 

ПК – 17 [2.2.1]

ВЫБОР

На рисунке для двух состояний D₁ и D₂ стрелками показаны зависимости …

– вероятности появления случайного параметра k в состояниях D₁ и D₂

– вероятности ошибок первого и второго рода

– кривые изменения параметра k в состояниях D₁ и D₂

– плотности вероятности появления параметра k в состояниях D₁ и D₂

 

ПК – 17 [2.2.1]

ВЫБОР

Метод определения оптимального порога k₀ принятия решений, определяемый из условия минимума суммы вероятностей ошибочных решений – это …

– метод Пирсона

– метод Байеса

– метод минимального среднего риска

– метод минимакса

 

ПК – 17 [2.2.1]

ВЫБОР

На рисунке параметр k₀ определяет …

– оптимальное пороговое значение параметра k

– среднее значение параметра k

– минимально допустимое значение случайного параметра k

– максимально допустимое значение случайного параметра k

 

ПК – 17 [2.2.1]

ВЫБОР

Площади заштрихованных областей на рисунке определяют …

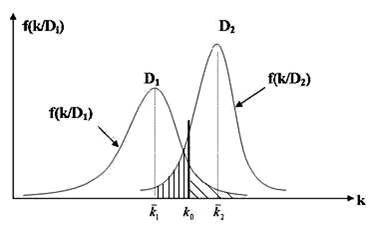
– вероятности исправного состояния

– условные вероятности ошибок первого и второго рода

– условные вероятности неисправного состояния

– недопустимые области эксплуатации

ПК – 17 [2.2.1]

ВЫБОР

Соотношение в методе минимального среднего риска, показанное на рисунке, для двух состояний D₁ или D₂ объекта при полученном параметре k, известных стоимостях ошибок C₁₂ и C₂₁ и безусловных вероятностей состояний P₁ и P₂, соответствует принятию решения …

– (k Î D₁)

– (k Î D₂)

– (k Î D₂ и D₁)

– (k Î D₂ или D₁)

 

ПК – 17 [2.2.1]

ВЫБОР

Соотношение в методе минимального среднего риска, показанное на рисунке, для двух состояний D₁ или D₂ объекта при полученном параметре k, известных стоимостях ошибок C₁₂ и C₂₁ и безусловных вероятностей состояний P₁ и P₂, соответствует принятию решения …

– (k Î D₁)

– (k Î D₂)

– (k Î D₂ и D₁)

– (k Î D₂ или D₁)

 

ПК – 17 [2.2.2]

ВЫБОР

Метод определения оптимального порога k₀ принятия решений, определяемый из условия равенства стоимостей ошибок первого и второго рода – это …

– метод Пирсона

– метод Байеса

– метод минимального числа ошибочных решений

– метод минимакса

ПК – 17 [2.2.2]

ВЫБОР

Соотношение в методе минимального числа ошибочных решений, показанное на рисунке, для двух состояний D₁ или D₂ объекта при полученном параметре k, равных стоимостях ошибок C₁₂ = C₂₁ и безусловных вероятностей состояний P₁ и P₂, соответствует принятию решения …

– (k Î D₂)

– (k Î D₂ и D₁)

– (k Î D₂ или D₁)

– (k Î D₁)

 

ПК – 17 [2.2.2]

ВЫБОР

Соотношение в методе минимального числа ошибочных решений, показанное на рисунке, для двух состояний D₁ или D₂ объекта при полученном параметре k, равных стоимостях ошибок C₁₂ = C₂₁ и безусловных вероятностей состояний P₁ и P₂, соответствует принятию решения …

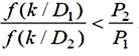
– (k Î D₂)

– (k Î D₂ и D₁)

– (k Î D₂ или D₁)

– (k Î D₁)

 

ПК – 17 [2.2.3]

ВЫБОР

Метод определения оптимального порога k₀ принятия решений, определяемый из условия следующего равенства (C₁₂·P₂ = C₂₁·P₁), – это …

– метод Пирсона

– метод максимального правдоподобия

– метод Байеса

– метод минимакса

ПК – 17 [2.2.3]

ВЫБОР

Соотношение в методе максимального правдоподобия, показанное на рисунке, для двух состояний D₁ или D₂ объекта при полученном параметре k, соответствует принятию решения …

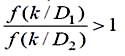
– (k Î D₂ или D₁)

– (k Î D₂ и D₁)

– (k Î D₁)

– (k Î D₂)

 

ПК – 17 [2.2.3]

ВЫБОР

Соотношение в методе максимального правдоподобия, показанное на рисунке, для двух состояний D₁ или D₂ объекта при полученном параметре k, соответствует принятию решения …

– (k Î D₁)

– (k Î D₂ или D₁)

– (k Î D₂ и D₁)

– (k Î D₂)

 

ПК – 17 [2.2.3]

ВЫБОР

Метод определения оптимального порога принятия решений, в котором оптимальный порог k₀ соответствует равенству f(k/D₁) = f(k/D₂), – это…

– метод минимакса

– метод Байеса

– метод Пирсона

– метод максимального правдоподобия

 

ПК – 17 [2.3.1]

ВЫБОР

Метод определения оптимального порога принятия решений, используемый в случае отсутствия сведений о безусловных априорных вероятностях диагнозов D1 и D2 и известных стоимостях ошибок C₁₂ и C₂₁, – это…

– метод минимакса

– метод минимума среднего риска

– метод Пирсона

– метод минимального числа ошибочных решений

 

ПК – 17 [2.3.1]

ВЫБОР

Метод определения оптимального порога k₀ принятия решений с использованием среднего риска R, определяемый из условия (dR/dk₀) = 0 и (dR/dP₁) = 0 – это…

– метод Пирсона

– метод Байеса

– метод минимакса

+ метод минимального среднего риска

 

ПК – 17 [2.3.1]

ВЫБОР

Метод определения оптимального порога k₀ принятия решений, соответствующего минимуму среднего риска R иопределяемый для максимально неблагоприятного значения вероятности P₁ – это…

– метод Пирсона

– метод Байеса

– метод минимального среднего риска

– метод минимакса

 

ПК – 17 [2.3.2]

ВЫБОР

Метод принятия решений, в котором оптимальный порог k₀ при известных стоимостях ошибок C₁₂ и C₂₁ соответствует отношению, представленному формулой на рисунке, – это…

– метод Пирсона

– метод минимакса

– метод минимального числа ошибочных решений

– метод минимума среднего риска

ПК – 17 [2.3.2]

ВЫБОР

Метод определения оптимального порога принятия решений, используемый в случае отсутствия сведений о безусловных априорных вероятностях диагнозов D1 и D2 и неизвестных стоимостях ошибок C₁₂ и C₂₁, – это…

– метод минимакса

– метод минимума среднего риска

– метод Пирсона

– метод минимального числа ошибочных решений

 

ПК – 17 [2.3.2]

ВЫБОР

Метод определения оптимального порога принятия решений k₀, в котором минимизируется вероятность пропуска дефекта P₁₂ и при заданном допустимом уровне вероятности ложной тревоги P₂₁ = A, – это …

– метод минимакса

– метод минимального числа ошибочных решений

– метод минимума среднего риска

– метод Пирсона

 

ПК – 17 [2.3.2]

ВЫБОР

Метод определения оптимального порога принятия решений, в котором оптимальный порог k₀ при заданной вероятности ложной тревоги P₂₁ = A определяется из соотношения, представленного формулой на рисунке, – это…

– метод Пирсона

– метод минимального числа ошибочных решений

– метод минимакса

– метод минимума среднего риска

 

ПК – 17 [2.3.3]

ВЫБОР

Метод определения вероятностей состояний, в котором число диагностических признаков обследования заранее не устанавливается и их проводится столько, сколько необходимо для принятия решения с определенной степенью риска, – это …

– метод Пирсона

– метод последовательного анализа

– метод минимакса

– метод минимума среднего риска

ПК – 17 [2.3.3]

ВЫБОР

Правило принятия решений о диагнозе объекта по методу последовательного анализа по n обследуемым признакам, если при допустимой верхней границе A соблюдается соотношение, показанное на рисунке:

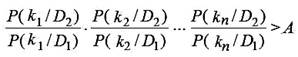
– (k Î D₁)

– (k Î D₂ или D₁)

– (k Î D₂)

– (k Ï D₂)

 

ПК – 17 [2.4.1]

ВЫБОР

Общее число состояний объекта диагностики, состоящего из N сменных неремонтируемых блоков при двух возможных состояниях каждого блока, определятся по формуле:

– S_N = 2^N

– S_N = N

– S_N = 2^N-1

– S_N = N-1

 

ПК – 17 [2.4.1]

ВЫБОР

Число неисправных состояний объекта диагностики, состоящего из N сменных неремонтируемых блоков при двух возможных состояниях каждого блока, определятся по формуле:

– S_N = 2^N-1

– S_N = 2^N-1

– S_N = N

– S_N = N-1

 

ПК – 17 [2.4.1]

ВЫБОР

Число неисправных состояний объекта диагностики, состоящего из N сменных неремонтируемых блоков при двух возможных состояниях каждого блока и возможности отказа только по одному блоку, определятся по формуле:

– S_N = 2^N-1

– S_N = N-1

– S_N = N

– S_N = 2^N-1

ПК – 17 [2.4.1]

ВЫБОР

Число состояний объекта диагностики, состоящего из N сменных неремонтируемых блоков при двух возможных состояниях каждого блока и возможности отказа только одного из них, определятся по формуле:

– S_N = 2^N-1

– S_N = N-1

– S_N = N

– S_N = N+1

 

ПК – 17 [2.4.1]

ВЫБОР

Вероятность неработоспособного состояния системы диагностирования, показанной на рисунке, с вероятностями отказов каждого блока равными соответственно q₁, q₂, q₃, q₄ при отказе блока 3 определяется по формуле:

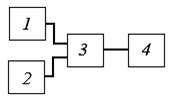
– P = (1- q₁)(1- q₂)q₃(1- q₄)

– P = (1- q₁)(1- q₂)(1- q₃)(1- q₄)

– P = q₁q₂(1- q₃)q₄

– P = 1-q₃

 

ПК – 17 [2.4.1]

ВЫБОР

Вероятность неработоспособного состояния системы диагностирования, показанной на рисунке, с вероятностями отказов каждого блока соответственно q₁, q₂, q₃, q₄ при одновременном отказе блоков 2 и 3 определяется по формуле:

– P = (1-q₃)(1- q₂)

– P = (1- q₁)q₂q₃(1- q₄)

– P = q₁(1- q₂)(1- q₃)q₄

– P = 1- q₂q₃

ПК – 30 [2.4.2]

ВЫБОР

Таблица для отбора минимально необходимого количества диагностических признаков – это …

– таблица функций неисправностей

– таблица состояний и проверок

– матрица состояний и признаков

– таблица результатов проверок

 

ПК – 30 [2.4.2]

ВЫБОР

Таблица, представленная на рисунке, – это …

– таблица состояний и проверок

– таблица результатов проверок

– таблица функций неисправностей

– матрица состояний и признаков

 

ПК – 30 [2.4.3]

ВЫБОР

Эффективность диагностического признака определяется …

– его информативностью

– скоростью проверки

– простотой регистрации

– таблицей результатов проверок

 

ПК – 30 [2.4.3]

ВЫБОР

Информативность диагностического признака определяется …

– вероятностью появления

– частотой появления

– количеством полученной информации

– матрицей состояний и признаков

ПК – 30 [2.4.3]

ВЫБОР

Количество информации, полученной после проверки диагностического признака, равно …

– условной энтропии системы после проверки

– информационной неопределенности системы

– вероятности появления признака

– разности энтропии системы до и после проверки

 

ПК – 30 [2.4.3]

ВЫБОР

Безусловная энтропия системы, которая может находиться в 8-ми равновероятных состояниях, равна …

 

ПК – 30 [2.4.3]

ВЫБОР

Информативность Z_xi отдельного признака x_i для различных состояний объекта, определяемая по количеству m -значимых результатов и n- незначимых результатов, определяется формулой:

– Z_xi = m/n

– Z_xi = m·n

– Z_xi = log₂(m+n)

– Z_xi = log₂(m/n)

 

ПК – 30 [2.5.1]

ВЫБОР

Если признак X₅ имеет приведенную в таблице одинаковую реакцию на все состояния, то необходимо …

– оставить признак для использования

– изменить код реакции признака на состояния

– признак удалить из рассмотрения

– определить дополнительный признак

ПК – 30 [2.5.1]

ВЫБОР

Если признаки X₆ и X₇ имеют приведенную в таблице одинаковую реакцию на различные состояния, то необходимо …

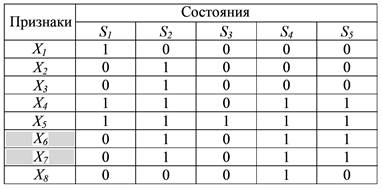
– удалить строку с одним из признаков

– удалить строки с обоими признаками

– оставить строки неизменными

– изменить коды реакций в строке с одним из признаков

 

ПК – 30 [2.5.2]

ВЫБОР

Информационный метод позволяет установить …

– общее число контролируемых параметров

– тип контролируемых параметров

– порядок контроля параметров

– необходимое число контролируемых параметров

 

ПК – 30 [2.5.3]

ВЫБОР

Таблица, представленная на рисунке, представляет собой …

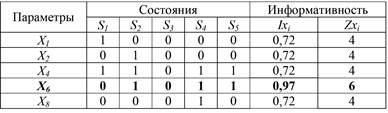
– матрицу информативности результатов проверок

– информационную таблицу сравнения состояний

– матрицу информативности признаков

– матрицу информативности состояний

ПК – 30 [2.5.3]

ВЫБОР

Таблицы, представленные на рисунке и обозначенные буквой «А», представляют собой …

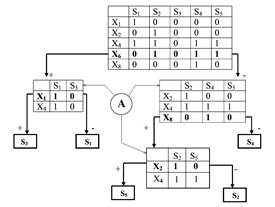
– матрицы измерения параметров

– матрицы изменения состояний

– матрицы изменения контролируемых параметров

– подматрицы информативности параметров

 

ПК – 30 [2.5.4]

ВЫБОР

Схема на рисунке – это …

– схема выявления состояний

– алгоритм поиска места отказа

– схема изменения состояний

– схема изменения контролируемых параметров

ПК – 30 [2.5.4]

ВЫБОР

На схеме, показанной на рисунке, знак «+» означает …

– добавление следующего параметра

– путь диагностирования

– путь изменения состояний

– параметр в норме

 

ПК – 30 [2.5.4]

ВЫБОР

Таблица, представленная на рисунке, представляет собой …

– матрицу неисправностей

– итоговую матрицу кодов

– матрицу параметров

– матрицу состояний

 

ПК – 30 [2.5.4]

ВЫБОР

Схема, показанная на рисунке, – это …

– алгоритм поиска места отказа

– порядок измерения параметров

– схема состояний

– схема отказов системы